Q7 Qubit - Ein Modell für Qubit-Algorithmen
Die gute Nachricht: Das ZBIT-Modell in der x-y-Koordinatendarstellung ist bereits das QBIT-Modell. Allerdings beschränkt auf 8 Zustände. R, X, H und M sind mit ihren Formeln dazu passend definiert. Mehr noch, man kann jeden Punkt (x,y) auf dem Einheitskreis als Zustand gelten lassen und die Operatoren liefern wieder einen gültigen Zustand. Und auch die Doppelt-Anwendung von X und H auf ein (x,y) liefert diesen Zustand wieder. (Wer Lust hat, kann regelrecht nachrechnen, dass HH(x,y) = (x,y) liefert und das gerne ins Kommentarfeld eintragen).
Eine ganze Reihe von Qubit-Algorithmen kann man bereits mit diesem ZBIT-Modell formulieren. Wer daher keine Lust hat, sich mit der Erforschung einer weiteren Box des Großen Experimentators zu befassen, kann daher auch zu Q8 über Qubit-Sprachgebrauch und Multi-Qubit-Modelle übergehen. Die nicht so gute Nachricht: Man verpasst dann die Möglichkeit, (x,y)-Zustände außer den 8 ZBIT-Zuständen zu entdecken. Mit dem ZBIT-Modell können wir keine Zustandsüberführung durchführen, die aus dem 8er-Set herausführt.
QBIT-Box
Dieses Mal konfrontiert uns der Große Experimentator mit einer ganz mysteriösen Box. Schwarz wie die Nacht (ohne Mond und Sterne) mit nichts auf den Flächen. Keine Touch-Felder, keine Klappe, keine Aufschrift ist zu erkennnen. Was sollen wir mit dieser Box anfangen, wie sie erforschen, wie damit experimentieren?
Nach längerem Überlegen und Probieren kommen wir auf die Idee, die Box mal ins Gefrierfach zu legen und zu kühlen. Nach kurzer Zeit hat sie sich tatsächlich verändert und sieht so aus:
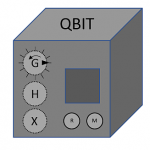
Die Box ist nun grau und zeigt die Aufschrift QBIT, hat die üblichen beiden Touchfelder X und H und zusätzlich eine Art Touch-Drehrad mit der Kennzeichung G, einer Skala und einer Markierung am Rand. Es gibt keine Klappe, die man auf und zumachen könnte. Dafür aber ein umrahmtes quadratisches Feld mit zwei Touch-Feldern M und R darunter. Wir vermuten gleich, dass das M für "Messen" steht, also dem früheren "Klappe auf", und R für "Reset", das offenbar "Klappe zu" ersetzt. Was das Drehfeld bedeutet, müssen wir wohl experimentell herausfinden.
Nach einiger Zeit in Zimmertemperatur verschwinden die Strukturen auf den Flächen wieder und die Box sieht aus wie vor der Kühlung. Da hat sich der Große Experimentator wohl eine besondere Schikane ausgedacht? Wir müssen also vor jedem Experiment die Box hinreichend tief kühlen, das erschwert Untersuchung und die Überprüfung unseres Modell-Ansatzes. Egal, da müssen wir durch. Vielleicht hilft ja eine Cool-Box ein wenig.
QBIT-Box Experimente
Wir überprüfen zunächst das Naheliegende - immer im gekühlten Zustand. Die Touch-Felder R, X, H und M bewirken das Entsprechende wie bei der ZBIT-Box:
R ---- M -> Dunkel, d.h. das quadratische Anzeigefeld wird schwarz
R ---- X ---- M -> Licht, das Anzeigefeld wird hell.
R ---- H ---- M -> Dunkel und Licht jeweils mit der Häufigkeit ungefähr 1/2
Kombinationen, wie X---H und H---H zeigen ebenfalls die von der ZBIT-Box bekannten Ergebnisse.
Neu ist das Touch-Drehrad G. Wir machen ein paar Versuche in Serie bei gleicher Einstellung. Dazu hilft die Skala am Rand. Wenn wir genau hinsehen, unterteilt die Skala den gesamten Kreis so ähnlich wie ein Ziffernblatt der Uhr. Allerdings haben die 12 Teilstriche noch Punkte jeweils auf der Mitte dazwischen. Ein Viertel des Umfangs hat damit 6 Markierungen, die analog zu einer Halbstunden-Skala sind. Im 360º Kreis entspricht das 15º. Wir bemerken, dass der "Zeiger" immer auf "3 Uhr" zurückspringt, wenn wir R betätigen, also scheint "3 Uhr" so etwas wie die Ausgangsposition des Dreh-Feldes zu sein.
Wir drehen den Zeiger auf "12 Uhr" bzw. 90° gegen den Uhrzeiger-Sinn (also mathematisch positiv) und berühren anschließend das "G" in der Mitte des Drehfeldes. Als Messergebnis leuchtet das Anzeigefeld hell. Wir wiederholen diese Operation mehrfach:
R ---- G90 ---- M -> L
und bekommen immer L. Nun liegt nahe, was wir, mehr oder wenniger systematisch, ausprobieren - immer mit ein paar Wiederholungen. Wir finden:
R ---- G45 ---- M -> Dunkel und Hell, vermutlich jeweils mit der Häufigkeit ungefähr 1/2
R ---- G00 ---- M -> Dunkel - das wußten wie schon, denn das ist genau das RM-Experiment von oben.
R ---- G30 ---- M -> D und L, mit einem Weiß/Schwarz-Häufigkeitsverhältnis von etwa 1:3.
R ---- G135 --- M -> D/L im Verhältnis etwa 1:1, also gleiches Ergebnis wie mit G45.
R ---- G180 --- M -> Dunkel für die Stellung "9 Uhr", also genau gegenüber der Ausgangsposition.
Mühselig, wie es sein mag, die Box muss systematisch erforscht werden. Wir machen die Experimente mit G für jeden der 12 Drehfeld-Teilstriche in Serie, 50 mal, und notieren die Häufigkeiten von Hell und Dunkel für jede Position. Die Grafik zeigt die Häufigkeit von Hell als Punkte über die 12 Teilstriche von "3 Uhr" bis "3 Uhr".
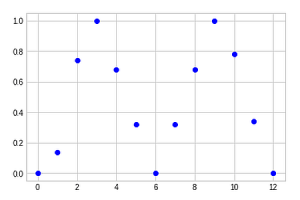
Ein gewisses Muster ist zu erkennen, wenn auch spärlich. Machen wir das Ganze noch einmal für die Zwischenpunkte und tragen die in eine Gesamt-Grafik mit 24 Positionen ein.
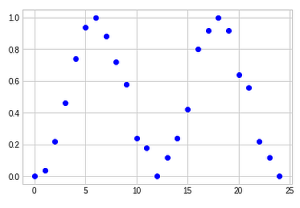
Man erkennt, dass die Punkte, die die Häufigkeit von L im Experiment zeigen, über die verschiedenen Dreh-Feld Einstellungen periodisch sind. Bei 12, d.h. "9 Uhr"-Stellung, ist die Häufigkeit wieder 0, bei 2 und 18 sind die Werte 1. Soweit man die trigonometrischen Funktionen kennt (sin, cos), kann man hier eine Art sin-Funktion erkennen. Da die Werte aber immer zwischen 0 und 1 liegen, sieht es eher nach sin² aus über 0 bis 360º, in 24 Schritten.
Bevor wir weitere Experimente machen, wollen wir versuchen, das Bisherige zu verstehen, d.h. uns ein passendes QBIT-Modell zu machen, das auch die Operation von G berücksichtigt.
Ein QBIT-Modell
Wir hatten in Q6 für das ZBIT bereits ein konsistentes Modell entwickelt und eine Darstellung gefunden, die uns Zustandsübergänge und die Zustand-Output Beziehung "rechnerisch", d.h. durch Formeln, zu formulieren ermöglichten. Die Zustände liegen dabei auf einem Einheitskreis in der x-y-Ebene.
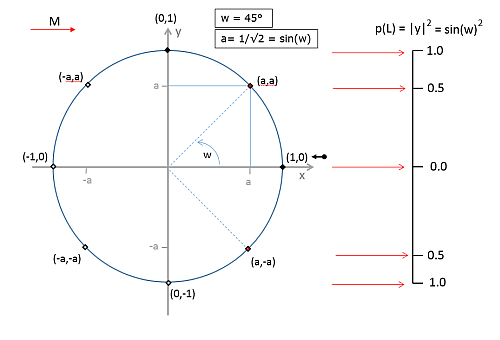
Für das QBIT-Modell müssen wir die Dreh-Operationen berücksichtigen. Die Einstellungen von "3 Uhr" (entspricht 0º) bis "12 Uhr" (entspricht 90º) liefern Ergebnisse für die Häufigkeit von L, die sich aufsteigend von 0 bis 1 verteilen. Von 90º bis 180º (9 Uhr) geht es umgekehrt von 1 nach 0. Und bei Einstellungfen von 180º bis 360º wiederholt sich das Geschehen. Wenn wir uns die p(L) Linie in der ZBIT-Modell Grafik ansehen, heißt das eigentlich nur, dass die experimentellen Ergebnisse auf der p(L)-Linie von der Mitte nach oben, dann nach ganz unten und zurück zur Mitte bewegen. Jeder Punkt auf der p(L)-Linie hat aber eine Entsprechung auf dem Einheitskreis - genauer, sogar zwei! (Mit zwei Ausnahmen.) Wir können daher als die Zustände eines QBIT-Modells alle Punkte auf dem Einheitskreis nehmen. Das umfasst natürlich auch automatische die 8 Zustände aus dem ZBIT-Modell.
Damit bekommen wir als QBIT-Modell-Beschreibung eine Erweiterung des ZBIT-Modells:
- Die Zustände sind alle Punkte auf dem Einheitskreis, d.h. alle (x,y), für die x² + y² = 1 gilt.
- Die Output-Werte bilden das Intervall [0,1], interpretiert als Wahrscheinlichkeiten p(L) für das Messergebnis L.
- Ein Zustand (x,y) ergibt als Output M(x,y) = |y|² = p(L) (wobei hier die das Betrags-Symbol | | unnötig ist). p(D) ist entsprechend x² = 1-y².
- R(x,y) = (1,0) und liefert p(L) = 0
- X(x,y) = (y,x). Wir leiten daraus ab, dass der Output M nach Anwendung von X p(L) = |x|² ergibt.
- H(x,y) = 1/√2(x+y,x-y). Was ist der Output p(L) direkt nach Anwendung von H auf (x,y)? (Wer Lust hat, usw.)
Wie beschreiben wir die Dreh-Feld Operation G? G "dreht" den Ausgangszustand (1,0) auf dem Einheitskreis entsprechend dem"Dreh-Winkel" (G für Gyro). Dazu müssen wir etwas mathematisch ausholen. Ein Zustand auf dem Einheitskreis (x,y) kann auch durch den Winkel w zum Ausgangspunkt beschrieben werden. Nämlich - da der Radius des Einheitskreises 1 ist - als x = cos(w) und y = sin(w). Damit hat der Modell-Zustand, der durch Drehen um den Winkel w ausgehend vom Zustand (1,0) erreicht wird die Koordinaten (x,y) = (cos(w),sin(w)). Die erfüllen die Gleichung für den Einheitskreis, klar, und das |y|² ist gleich sin(w)². Also setzen wir
- G(w) = (cos(w),sin(w)), wobei w der Dreh-Winkel von (1,0) aus ist.
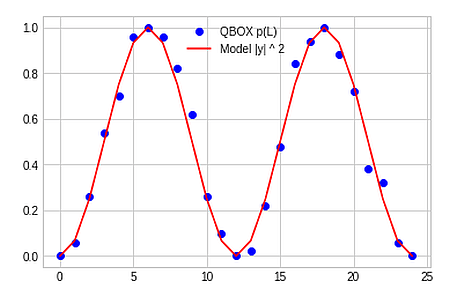
Wir können damit das Modell einfach berechnen und den Output, das p(L), für alle Drehfeld-Einstellungen von 0 bis 360 in die Grafik der experimentellen Ergebnisse einzeichnen. Die rote Linie repräsentiert die Funktion sin(w)² und passt (zumindest visuell) hervorragend zu den blauen Punkten. Wir haben damit eine "statistische Bestätigung" unseres Modells.
Vorhersagen und Erklärungen
Was passiert, wenn wir zwei G hintereinander schalten?
1. R ---- G90 --- G45 ---- M -> 0.5 (Modell), 49:51 Experiment
2. R ---- G45 --- G90 ---- M -> 0.5 (Modell), 52:48 Experiment
3. R ---- G60 --- G45 ---- M -> 0.93 (Modell), 4:96 Experiment (D:L)
4. R ---- G105 --- M -> 0.93 (Modell), 9:91 Experiment (D:L)
Offenbar ist der Effekt zweier Drehungen der gleiche wie eine Drehung um die Summe der Winkel, in der Theorie wie - statistisch - im Experiment.
Wir wissen, dass X so wirkt, dass die Koordinaten vertauscht werden.
5. R ---- G60 ---- M -> 0.75 (Modell), 22:78 Experiment (D:L)
6. R ---- X ---- G60 ----M -> 0.25 (Modell), 74:26 Experiment (D:L)
7. R ---- G60 ---- X ----M -> 0.25 (Modell), 75:25 Experiment (D:L)
Das X vor oder nach der Drehung vertauscht die Koordinaten und damit die theoretischen Wahrscheinlichkeiten für D und L.
Nun noch ein paar Kombinationen mit H:
8. R ---- G60 ---- H ---- H ---- M -> 0.75 (Modell), 24:76 Experiment (D:L)
Das entspricht dem Ergebnis von Versuch 5. D.h. das doppelte H hebt sich auf - wie wir das ja schon aus dem ZBIT-Modell kennen. Aber was macht ein einzelnes H?
9. R ---- G60 ---- H ---- M -> 0.067 (Modell), 93:7 Experiment (D:L)
Vorhersage und Experiment passen recht gut zusammen. Wir können aber das Ergebnis aus dem Modell "errechnen", indem wir die Formeln anwenden.
Die Drehung des Ausgangszustands (1,0) um 60º liefert den Punkt
(cos(w),sin(w)) mit w=60º
auf dem Einheitskreis. H bedeutet, darauf die Formel 1/√2(x+y,x-y) anzuwenden, also
H(cos(w),sin(w)) = 1√2(cos(w)+sin(w),cos(w)-sin(w)).
Dieser Zustand wird gemessen (in Serie von 100). Mit M bedeutet das
p(L)=|y|²=1/2*(cos(w)-sin(w))².
Das ergibt (berechnet z.B. mit Wolfram Alpha) p(L) = 0.0669. Die Modell-Zustände, -Übergänge und -Outputs kann man berechen - die Ergebnisse der QBIT-Box dagegen NICHT!
10. R ---- H ---- G60 ---- M -> Liefert in Experiment-Serien Ergebnisse um 8:92 für (D:L). Das sieht aus wie das Ergebnis von 3., oben.
Ob das stimmt, können wir per Modell herausfinden. R setzt den Anfangszustand (1,0), H macht daraus 1/√2(x+y,x-y)=1/√2(1,1), das kennen wir schon. Dieser Punkt liegt auf dem Einheitskreis mit dem Winkel 45º, da die x- und y-Koordinate gleich sind. D.h. H macht mit (1,0) das Gleiche wie eine Drehung um w=45º. Anschließend "dreht" G60 weiter auf 45+60=105º. Und das ist genau das, was wir in Versuch 3. hatten. Damit ist das theoretische Ergebnis wieder p(L)=0.93, passend zum Experiment. Aber Achtung! H ist nicht generell mit G45 gleich zu setzen. H ist keine Drehung um einen festen Wert. Wo H(x,y) liegt, hängt von (x,y) ab. Wer Lust hat kann überlegen, was passiert, wenn wir nach R erst ein X einsetzen (und das in einen Kommentar schreiben).
Auf diese Weise kann man viele weitere 1-Qubit Algorithmen formulieren und per Modell untersuchen. Leider ist der Gegenstand unsere Experimente nur ein virtueller. Der G.E. hat uns keine Handhabe gegeben, Experimente anders als immer mit der gleichen Routine zu machen: Kühlen, Reset, Operationen anwenden, Messen und das Ergebnis im Hell/Dunkel-Feld beobachten. Protokollieren und Statistik machen. (Wer wissen will, wie die Ergebnisse der obigen Mess-Serien zustande gekommen sind, kann das im nächsten Blog-Abschnitt kennen lernen.)
Die Vielfalt der Bezeichnungen
Eines hat in der Abfolge der Modellierungsansätze vermutlich irritert: die offensichtliche Beliebigkeit der Darstellung und Bezeichnung der Modell-Zustände. Nun, das hatte einen guten Grund. Es sollte zeigen, dass es
(a) verschiedene Modell-Beschreibungen für die gleiche Sache gibt,
(b) keine davon per se die "Wahre" ist und
(c) es der "Sache" egal ist, welche Beschreibung wir wählen, sofern sie nicht im Widerspruch zu den Experimenten steht.
Wir können daher bei der Modellwahl auf andere Eigenschafte achten, z.B. ob die Begriffe leicht zu verstehen oder zu merken sind, ob man damit leicht operieren bzw. rechnen kann, oder ob uns eine der Möglichkeiten einfach mehr Spaß macht, besser "in der Hand liegt".
In der Qubit-Algorithmik findet man daher mindestens 3 Standard-Beschreibungsansätze für Qubits. Wir werden darauf später teilweise noch eingehen können.
Zunächst wollen wir aber mal in unserem eigenen Zoo von Modellen Klarheit schaffen, vom BIT bis zu QBIT. Dazu zeigt folgende Tabelle, welche Zustandsbezeichnungen in den verschiedenen Ansätzen sich entsprechen.
| Uhr | Grad | π | π/2 | x-y-KoS | p(L) | ZBIT | BIT | Alice | Qubit |
| 3:00 | 0º | 0 | 0 | (1,0) | 0 | [00] | [0] | Alice | |0> |
| 2:00 | 30º | 1/6 | 1/3 | (√3/2,1/2) | 1/4 | -- | -- | -- | |
| 1:30 | 45º | 1/4 | 1/2 | (1/√2,1/√2) | 1/2 | [01] | -- | Charly | |+> |
| 1:00 | 60º | 1/3 | 2/3 | (1/2,√3/2) | 3/4 | -- | -- | -- | |
| 12:00 | 90º | 1/2 | 1 | (0,1) | 1 | [11] | [1] | Debbie | |1> |
| 9:00 | 180º | 1 | 2 | (-1,0) | 0 | -- | -- | -- | |
| 6:00 | 270º | 3/2 | 3 | (0,-1) | 1 | -- | -- | -- | |
| 4:30 | 315º | 7/4 | 7/2 | (1/√2,-1/√2) | 1/2 | [10] | -- | Bob | |-> |
| hh:mm | wº | φ | θ | (x,y) | |y|² | -- | -- | -- | x|0>+y|1> |
Jede Spalte entspricht einer der Beschreibungsmöglichkeiten, die Einträge in einer Zeile entsprechen einander. Die erste Spalte zeigt Werte unseres Uhren-Bildes, mit dem Ausgangszustand auf 3 Uhr. Die zweite Spalte zeigt die entsprechenden Werte in Grad, gegen den Uhrzeigersinn. Statt Grad-Angaben kann man auch den Kreis mit Winkelangaben in π kennzeichnen. Die Spalte x-y-KoS gibt die entprechenden Koordinaten wieder, p(L) die zugehörige Wahrscheinlichkeit für L. Im ZBIT- und BIT-Modell hatten wir nur 4 bzw. 2 Zustände gekennzeichnet. Für das ZBIT die Zustände sogar mal mit Namen gekennzeichnet. Die letzte Spalte und die Spalte π/2 sind Zustandsschreibweisen, die wir noch kennen lernen werden. Sie gehören zu den erwähnten Standard-Beschreibungen für Qubits. Wenn man mal nicht weiß, was was ist, hat man hier eine Tabelle zum Nachschlagen.
Die letzte Zeile stellt die verwendeten Symbole für einen allgemeinen Zustand in der jeweiligen Schreibweise dar. Es fällt auf, dass es für das ZBIT- und BIT-Modell keinen "allgemeinen" Zustand gibt. Es sind stets die 4 bzw. 2 Zustände und nichts "dazwischen".
Wir sind jetzt in der Qubit-Welt angekommen, zumindest in einer der Qubit-Welten. Mit einem Qubit kann man algorithmisch recht wenig anfangen, vergleichbar einem Programm mit nur einer Variablen. Interessanter werden Qubit-Algorithmen, die mehrere Qubits umfassen - in einem sog. Qubit-Register. Das werden wir - nach einer kleinen Pause natürlich - im nächsten Abschnitt kennen lernen. Und zwar durch kleine praktische Beispiele von der Art "Hello Qubit World" in Q2, ausgeführt auf dem IBM Q Experience Quantencomputer (bzw. dem Simulator).
Hier geht's weiter.
Ach ja, wofür steht wohl QBIT auf der Box? Vorschläge gerne in den Kommentarfelden.
Q6 Zwischenspiel - ZBIT-Spielereien
Hier wollen wir mit dem verbesserten ZBIT-Modell aus Q5 ein wenig rumspielen, um mit dem Modell und den Definitionen ein wenig vertrauter zu werden. Um so leichter fällt dann der letzte (kleine) Schritt zum Qubit. Wegen des letzten Abschnitts ist dieser Blog etwas länger geraten. Dafür führt er uns aber zu einer Modell-Darstellung, die schon die für das Qubit-Modell sein wird. Wer keine Lust hat zum Spielen, kann auch einfach nur einen Kaffee trinken und gleich mit dem nächsten Blog weitermachen.
Wir hatten schon festgestellt, dass die inneren Zustände eigentlich beliebig wählbar sind, vorausgesetzt, die Maschinen-Tabellen (Output und Zustandsübergänge) sind konstistent.
1. Alice, Bob, Charly und Debbie
Statt [00] usw. können wir z.B. Namen nehmen:
Alice, Bob, Charly und Debbie statt [00], [10], [01], [11]. Wenn wir die vier dann als Ecken eines Quadrats aufstellen, etwa in der Sporthalle, können wir das Modell als Ballspiel beschreiben:
- Jede Runde beginnt bei Alice, sie hat den Ball (Operation R)
- Jeder spielt den Ball entsprechend den Regeln von X und H.
- Jeder ist dabei frei, welche der Regel sie oder er "werfen" will
- Irgendwann pfeift der Referee ab (M)
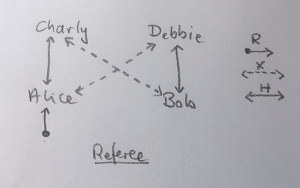Die Grafik illustriert das Set-up. Die Pfeile zeigen, wie X und H gespielt werden dürfen. Da die Personen formal Zustände sind, zeigt die Grafik ein sog. Zustandsüberführungs-Diagramm, ein Wort, das man üben muss.
Wir haben noch nicht gesagt, was D, L und P sein sollen. Da wir die inneren Zustände und Übergänge beim Ballspiel beobachten, könnten wir trivialerweise festlegen: D, wenn der Ball bei Abpfiff bei Alice ist, L, wenn er bei Debbie ist und P, wenn er bei einem der beiden anderen ist. Das ist nicht beonders interessant.
Wie wäre es, wenn bei Abpfiff der Ball in einen Basketball-Korb geworfen werden muss? Das ganze Spiel findet hinter einem Vorhang statt, sodass wir es nicht sehen können. Allein den Wurf auf den Korb können wir sehen. Dabei bedeutet D, dass der Ball niemals versenkt wird (Alice), L, dass er mit Sicherheit reingeht (Debbie), und P, dass er manchmal trifft und manchmal nicht, im Verhältnis 1:1.
Fragen: Können wir herausfinden, wer den Ball zum Korb wirft? Wie wäre es, wenn wir dem Team bzw. dem Referee Spielpläne vorgeben würden (Algorithmen)? Wie könnte ein "autonomes" Spiel aussehen? D.h. jeder Spieler entscheidet (zufällig) welchen der möglichen Würfe (R, X, H, M) er oder sie macht.
Wer Lust hat, kann Überlegungen oder Antworten als Kommentar einfügen.
Nun gut, lassen wir die vier weiter spielen und wenden uns einer Darstellung zu, mit der wir das ZBIT-Modell simulieren können.
2. Ein ZBIT-Box Simulationsmodell
Wir haben im Beitrag "Etwas ist anders - Hello Qubit World" die Partitur eines QuBit-Algorithmus gesehen - ohne zu wissen, worum es geht. Solche Partituren können, wenn sie fehlerfrei sind, von Quanten-Computern oder auch von QC-Simulatoren abgearbeitet werden. Es wäre doch interessant, wenn wir die ZBIT-Experimente in diese Form bringen könnten und sie dem Simulator vorlegen könnten.
Da die Experimente mit den ZBIT- und BIT-Modellen schon in Anlehnung an die "Partitur-Form" beschrieben wurden, sollte es uns tatsächlich leicht fallen.
Die Modell-Beschreibung für den QC-Simulator ändert sich kaum: X und H werden vom Simulator "verstanden", das R gibt es nicht explizit, sondern jede Partitur beginnt mit dem Ausgangszustand. Der wird im Simulator mit |0> gekennzeichnet statt mit [00], aber die Namen der inneren Zustände sind ja unwesentlich. (Was |0> bedeutet, werden wir später sehen.) Das Anzeige-Symbol ("Tacho-Nadel") steht für die Operation M (Messen).
Anders als bei den bisherigen Modell-Beschreibungen können wir nichts über die inneren Zustände des Simulators wissen. Die Zeile der Zustandsübergänge in den bisherigen Experimenten ist nicht verfügbar - jedenfalls beim QC. Die Messergebnisse des Simulators können '0' oder '1' sein, das entspricht dem D und L im ZBIT-Modell. Was wir für P bekommen sehen wir im Experiment.
Wir nehmen das ZBIT-Vorhersage-Experiment aus dem vorausgehenden Blog:
R ------ H ----- X ----- H ---- H ----- M -> P
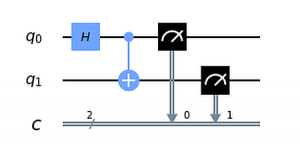
und bilden es ab auf den QC-Simulator (hier: IBM Q Experience Circuit Composer).
Mit dem QC-Simulator können wir dieses Experiment einmal durchführen und erhalten:
{'0': 1}. Wir wiederholen und bekommen wieder ein {'0': 1}, dann ein {'1': 1}. Das bedeutet, die ersten drei Experiment-Durchläufe resultierten jeweils in einer '0', bzw. einer '1'. Wir bekommen also D oder L als Output. Wie bei der ZBIT-Box machen wir jetzt Mehrfach-Experimente, z.B. eine Serie von 50 Durchläufen. Das Ergebnis:
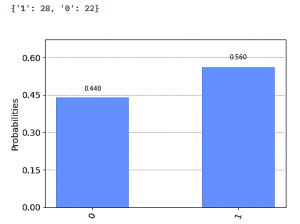also 28 mal L und 22 mal D in unserer ZBIT-Interpretation.
Das sieht schon recht spannend aus. Im Prinzip könnten wir alle bisherigen Experimente mit dem BIT-Modell und dem ZBIT-Modell in dieser Weise simulieren. Damit kommen wir dem Konzept von Qubit-Algorithmen schon sehr nahe.
Und wir gewinnen eine wichtige Erkenntnis: ZBIT (das verbesserte) und BIT sind Teilmodelle des - hier noch unbekannten - Qubit-Modells.
Wer Lust hat, kann nicht nur Fragen und Antworten als Kommentar unten anfügen, sondern auch unter IBM Q Experience sich registrieren und schon mal im Circuit Composer stöbern. Wir schauen uns das in einem späteren Blog noch mal näher an. Eine ähnliche Umgebung bietet auch Google an mit Cirq.
Nun wenden wir uns einer Darstellung zu, mit der wir das ZBIT-Modell mit einfachen Formeln berechnen können.
3. Ein Modell mit Formeln
Wir wollen nun versuchen, die Zustände so zu definieren, dass man mit ihnen "rechnen" kann. Statt in den Automaten-Tabellen die Zustandsübergänge nachzusehen, wollen wir sie mit einfachen Formeln berechnen können. Das gleiche für die Outputs.
Eine naheliegende Idee wäre es, die Ziffern in den Zuständen [00] usw. tatsächlich als Zahlen aufzufassen und dazu auch die Output-Ergebnisse in Zahlen umzuwandeln: D entspricht 0, L entpricht 1, und P dem Wert 1/2. Diese Werte können verstanden werden als Wahrscheinlichkeiten, dass wir Licht sehen, wenn wir die Klappe öffnen. Wir schreiben dafür p(L).
Allerdings hatten wir [00] usw. eigentlich nur als "Label" für die Zustände eingeführt und nicht als arithmetische Größen. Daher wäre es ein erstaunlicher Zufall, wenn wir damit ein konsistentes arithmetisches Modell bilden könnten.
Tatsächlich geht das aber, bis zu einem gewissen Punkt. Wer sich davon überzeugen will: es gibt einen Annex zu Q6, in dem das dargestellt wird. Wenn wir allerdings das Modell erweitern wollen, z.B. um Zustände, die p(L) = 1/4 als Output liefern, gibt es Schwierigkeiten.
Wir geben uns daher etwas mehr Freiheit bei der Definition eines rechnerischen Modells, indem wir die Zustände ("Labels"), in ein x-y-Koordinatensystem einbetten. (Wir erinnern uns, dass wir mit den zwei-ziffrigen Zuständen in Q5 so etwas wie 2-dimensionale Zustände eingeführt hatten.) Die Zustände werden dann zu Punkten in der x-y-Ebene.
Wir halten die Bezeichnungen [00] bzw. Alice zunächst einmal bei. Sie benennen die Punkt, so wie man Punkte A, B und C eines Dreiecks in der Ebene benennt und mit Koordinaten versieht. Trotzdem können die 0-en und 1-en etwas verwirrend wirken. Die Punkte werden mit ihren Koordinaten in normalen Klammern geschrieben, also z.B. (1,0), die [00] in eckigen Klammern sind die Label der Punkte, ebenso wie die Namen Alice etc.
Das Einfachste ist, die beiden Zustände [00] und [11] - die ja auch die BIT-Zustände repräsentieren - auf die Koordinaten-Achsen zu platzieren. [00] als Punkt auf der x-Achse bei 1: (x,y) = (0,1). Und [11] entsprechend auf der y-Achse: (x,y) = (1,0). Das Diagramm zeigt wie.
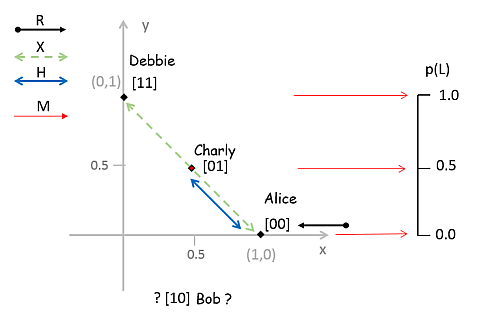
Wo würden wir dann die Zustände [10] und [01] positionieren? Nun, das können wir bereits "ausrechnen". Schauen wir uns dazu zunächst die passenden Formeln für die Wirkung der Operatoren R, X und H an.
R ist einfach: R(x,y) = (1,0). Das Reset überführt jeden Zustand in den Ausgangszustand, der jetzt die Koordinaten (0,1) hat.
Auch X ist nicht schwer: X(x,y) = (y,x). X als "Switch" vertauscht die Koordinaten. Das passt schon mal für die beiden vorgegeben Zustände (1,0) <-> (0,1).
Wir haben uns noch nicht um den Output gekümmert. Der Output von (1,0) (i.e. [00]) muss p(L) = 0 sein, der vom (0,1) (i.e. [11]) entspechend p(L) = 1. Es liegt daher nahe, die y-Koordinate als p(L) zu übernehmen. Die x-Koordinate wäre entsprechend als Wahrscheinlichkeit für D zu interpretieren: p(D).
Hieraus folgt direkt und zwingend: p(L) + p(D) = 1.
Damit bekommen wir folgende Bedingungen für die Zustände [10] und [01]:
(1) Sie müssen so positioniert werden, dass die Summe ihrer beiden Koordinaten 1 ergeben.
(2) Der zugehörige Output muß 1/2 ergeben; die y-Koordinate muss also 1/2 sein.
(3) Wegen der Wirkung von HH, müssen H[00] = [01] und H[11] = [10] unterschiedliche Koordinaten haben.
Man sieht sofort, dass diese Bedingungen unvereinbar sind: [01] kann mit den Koordinaten (1/2,1/2) die Bedingung (1) und (2) erfüllen. Es gibt aber keinen weiteren Punkt, der (1) und (2) erfüllt.
Wir ändern daher die Output-Definition: M (x,y) = p(L) = |y|, d.h. die Wahrscheinlichkeit für L ist der Absolutbetrag von y. Die Bedingungen (1) und (2) werden dann zu
(1') Die Summe der Beträge der Koordinaten muss 1 sein: |x|+|y| = 1. Und
(2') Der Betrag der y-Koodinate muss 1/2 sein
Wenn wir dann [10] mit den Koordinaten (1/2,-1/2) versehen, werden alle drei Bedingungen erfüllt. (Siehe Grafik.)
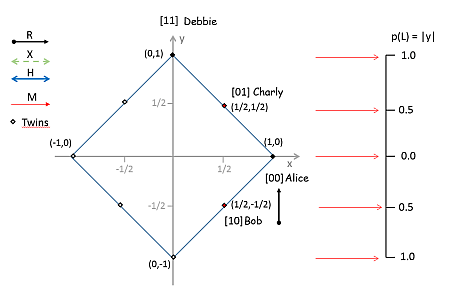
Weiter stellen wir fest, dass aus der Anwendung X und H auf schon bekannte Zustände neue Punkte hervorgehen, die wir ebenfalls als Zustände zulassen müssen. So muß z.B. mit (1/2,-1/2), den Koordinaten für [10], auch X(1/2,-1/2) = (-1/2,1/2) = -(1/2,-1/2) ein zulässiger Zustand sein. Wenn H(1/2,-1/2) wieder (0,1) sein soll (doppelte H Anwendung auf [11]), dann muss H(-1/2,1/2) = (0,-1) zulässig sein. Und X(0,-1) = (-1,0) = -(1,0) ebenso. Das Diagramm zeigt die Zustände als Punkte, die Pfeile für die Operatoren sind wegen der Übersichtlichkeit nicht eingezeichnet. Man kann aber, wenn man Lust hat, selbst versuchen, diese Zustandsübergänge einzuzeichnen (gedanklich), soweit es geht.
Das ist zunächst einmal überraschend: Wenn wir die 4 Zustände des ZBIT-Modell durch Punkte im (x,y)-Koordinatensystem darstellen wollen, erweitert sich das Modell zwangsläufig auf 8 Zustände! In unserem ZBIT Ball Game oben, würden dann Alice, Bob, Charly und Debbie jeweils einen Zwilling bekommen, Twin-Alice usw. Eigentümlich - aber niemand zwingt uns, bei einem Modell für die ZBIT-Box mit nur 4 Zuständen auszukommen. Vier ist das Minimum, aber 8 geht auch. Im Diagramm sind die "Twins" als helle Punkte eingezeichnet. Frage: Welcher Punkt ist Twin von wem?
Damit haben wir für das Koordinaten-basierte Modell:
- Die Zustandsmenge
- Die Wirkung von R und X als Formel
- Die Zustand -> Output Abbildung M mit der Interpretation als p(L), Wahrscheinlichkeit für L als Messergebnis
Was fehlt, ist die Formel für H. Wir hatten festgelegt, dass (1,0) (Label [00]) durch H in (1/2,1/2) überführt werden soll und (0,1) (Label [11]) in (1/2,-1/2). Eine naheliegende Formel für H wäre: H(x,y) = 1/2 (x+y, x-y). Sie liefert für (1,0) und (0,1) genau das, was sie soll. Aber wie sieht es mit (1/2,1/2) und (1/2,-1/2) aus. H auf diese Zustände angewandt müsste ja wieder (1,0) bzw. (0,1) ergeben.
Jedoch: H(1/2,1/2) = 1/2 (1/2+1/2, 1/2-1/2) = 1/2 (1,0). Den gleichen Widerspruch erhalten wir für (1/2,-1/2). Der Faktor 1/2 macht die Inkonsistenz aus. Wenn wir allerdings den Faktor 1/2 in der Definition von H weg lassen, bekommen wir für (1,0) und (0,1) schon gleich falsche Ergebnisse.
Was tun? Vielleicht etwas dazwischen - zwischen 1/2 und 1? Wie es die Mathematiker gerne machen, wenn man sich nicht entscheiden kann, setzt man anstelle von 1/2 eine Variable, sagen wir a, und versucht, dafür einen passenden Wert zu bestimmen. Das ist sehr elegant. Probieren wir also: H(x,y) = a*(x+y,x-y).
H(1,0) ergibt dann nicht mehr (1/2,1/2) sondern (a,a), was immer a auch ist. Entsprechend H(0,1) = (a,-a). Wenn wir darauf wieder H anwenden, bekommen wir H(a,a) = a*(a+a,a-a) = a*(2a,0) und H(a,-a) = a*(a+(-a),a-(-a)) = a*(0,2a). Andererseits muss H(a,a) = (1,0) sein, also a*2a = 2a² = 1 oder a = 1/sqrt(2). Das klappt auch mit der zweiten Bedingung. Très chic !
Allerdings stehen wir damit wieder am Anfang. Wir müssen die drei Spiegelpunkte oben wieder neu festlegen. Aber dieses Mal lohnt sich die Spielerei; denn wir haben hiermit automatisch die grundlegenden Komponenten für ein Qubit-Modell in Q7 abgeleitet.
- Die 8 Zustände sind (1,0), (0.1), (-1,0), (0-1) und (a,a), (-a,a), (-a,-a), (a,-a) mit a = Wurzel aus 1/2. Alle diese Zustände liegen auf einem Kreis mit Radius 1.0 im x,y-Koordinatensystem. Sie erfüllen die Bedingung x² + y² = 1, die Gleichung des Einheitskreises.
- R und X sind genau wie zuvor definiert, und H als H(x,y) = a*(x+y,x-y).
- Wie ist die Zustand-Output Beziehung? Jetzt ergibt M(x,y) = y² das p(L), die Wahrscheinlichkeit für L bei einer Messung. Und p(D) ist entsprechend x² = 1-y², was ja für alle Zustände auf dem Einheitskreis stimmt.
Das Diagramm zeigt das ZBIT-Modell mit diesen Festlegungen.
Der letzte Abschnitt war sicher keine einfache Spielerei mehr. Aber wir haben es geschafft. Und, wie wir sehen werden, gleichzeitig DAS Werkzeug für Qubit-Algorithmen gefunden.
Frage: Wie würde das ZBIT Ball Game aussehen, wenn wir die vier neuen Spieler ins Feld bringen würden - nennen wir sie Twin-Alice, Twin-Bob, Twin-Charly und Twin-Debbie? Wer Lust hat usw.
Im nächsten Blog, versprochen, kommen wir aber zum QuBit-Modell - zumindest in einer ersten Form.
Fortsetzung folgt - Stay tuned!
Q3 Vom Bit- zum Qubit-Modell
Um herauszufinden, was das Hello Qubit World eigentlich macht, müssen wir uns doch erst mal ein Bild davon machen, was ein Qubit sein soll - im Vergleich zu einem Bit. Wir entwickeln dazu ein verständliches Modell eines Qubits, das wir verstehen können ohne die physikalische Quantentheorie verstehen zu müssen.
B I T
Stellen wir uns vor, der Große Experimentator stellt uns einen schwarzen, würfelförmigen Kasten hin, auf dem oben die Buchstaben "B I T" stehen. Der Kasten hat vorne rechts eine Klappe, die man nach unten öffnen kann. Und ein Touch-Feld markiert mit einem "X" links daneben.
Was machen wir? Was zuerst? Die Klappe auf oder das Feld berühren? Egal - wir öffnen die Klappe und sehen ... nichts, es ist dunkel in der Box. Wir schließen die Klappe und öffnen sie wieder. Keine Änderung. Wir berühren das Touch-Feld: es tut sich nichts. Wir schließen die Klappe, berühren das Feld, machen die Klappe auf: Licht. Aha! Klappe zu, Klappe auf: wieder Dunkel. Aha! Es kristallisiert sich eine Vermutung heraus. Und jetzt werden wir systematisch:
- Ausgangspunkt: Klappe zu
- Klappe auf: Dunkel
- Wiederholung: es bleibt Dunkel
- Ausgangspunkt: Klappe zu
- X berühren, Klappe auf: Licht
- Wie 4. und 5., aber zweimal hintereinander X berühren: Dunkel
- Wiederholungen 1.-3. bzw. 4. und 5. bzw. 7. zur statistischen Absicherung.
Das lässt uns folgende empirische Regel vermuten:
Macht man nur die Klappe auf, ist es dunkel. Berührt man vorher das Touch-Feld, sieht man Licht. Berührt man es mehrmals hintereinander, heben sich jeweils zwei X gegeneinander auf.
(Jetzt wissen wir auch, warum der Große Experimentator den Kasten mit BIT beschriftet hat: Abkürzung für "BIT Intelligence Tester". War aber ziemlich einfach.)
Wie die BIT-Box das macht, wie sie konstruiert ist, können wir leider nicht wissen. Selbst wenn wir sie zerschlagen würden, hätten wir nur ein paar unverständliche Brocken. Wir können aber ein Modell davon machen, zunächst auf Papier.
Das BIT-Modell
Wir legen fest, BIT hat eine interne Zustandsvariable. Die kann zwei Werte (Zustände) annehmen. Mit der gültigen Operation X , das entspricht dem Touch-Feld-Berühren bei der Box, lässt sich der Modellzustand wechseln. Die Operation R, das dem Schließen der Klappe entspricht, stellt einen festgelegten Anfangszustand von BIT her (Reset). BIT gibt uns je nach Zustand ein Signal als Output, das "Licht" oder "Dunkel" entspricht. Dazu müssen wir aber etwas tun: bei der Box die Klappe öffnen und nachschauen. Wir können das als Messen (M) des BIT-Zustands auffassen. Die Operation X kann nur "bei geschlossener Klappe" ausgelöst werden, d.h. wir können die Wirkung der Operation nicht unmittelbar beobachten, ebenso wenig wie die internen Zustände. Wir erschließen beides aufgrund des Outputs, den wir durch M (Klappe auf) bekommen.
Nach dieser Modellbeschreibung können wir leicht eine weiße Box konstruieren und bauen. Das einfachste ist eine kleine Lichtanlage mit einem (inneren) Schalter, der durch "Knopfdruck" X geschaltet wird - aber nur wenn die Beobachtungsklappe geschlossen ist.
Wir können es aber etwas "mathematischer" beschreiben, so dass wir im Prinzip das BIT-Modell "berechnen" können.
- Wir kennzeichen die beiden Zustände mit [0] und [1]. Die Ziffern haben keine Bedeutung; wir könnten die Zustände auch Paul und Paula nennen.
- Wir setzen [0] als den Startzustand
- Die Outputs des Modells werden als D und L abgekürzt, für Dunkel und Licht
- Die beiden Operationen X und R hatten wir schon eingeführt: Touch-Feld Berühren bzw. Klappe zu. Ihre Wirkung auf den BIT-Zustand ist wie folgt:
R: [0] -> [0] und [1] -> [0] (Reset)
X: [0] -> [1] und [1] -> [0] (Switch)
Das Messen des BIT-Zustands (Klappe auf und schauen) kürzen wir mit M ab. Messen des Zustands ergibt
M: [0] -> D und [1] -> L
Ein Experiment mit diesem Modell kann dann z.B. so beschrieben werden: R--X--X--M . Was bedeutet das? Im Modell können wir die Zustandsfolge und den Output nun "berechnen":
R -----X-----X-----M
[0] -> [1] -> [0] -> D
Der Output nach M ist - D. Beim entsprechende Experiment mit der black box können wir davon nur Dunkel beobachten. das entspricht dem D als Output. Die Operationen können wir auslösen, aber ihren Effekt nur erschließen, z.B. aus
R----M -> D
R----X----M -> L
Was ergibt folgender Algorithmus?
R----X----X----R----M
Nichts - diese Abfolge ist offenbar nicht zulässig. Solange die Klappe zu ist kann sie nicht wieder geschlossen werden. Es gibt also gewisse Regeln zu beachten in der Aufeinanderfolge von Operationen. Nicht alles ist möglich, bzw, "wohldefiniert".
R----X----M----R----M ist dagegen möglich. Der Output ist D - klar?
Nicht von ungefähr erinnern diese Operations-Linien schon an die Diagramme von einfachen Qubit-Algorithmen im letzten Abschnitt.
Algorithmen
Wir können mit dem BIT-Modell bereits kleine Algorithmen formulieren und - gedanklich - mit der BIT-Box manuell durchführen. Ein Beispiel:
R---X---M---R---M---R---X---M liefert an den Messpunkten (M): L D L
oder Beeb Bib Beeb, den Morse-Code für den Buchstaben 'K'.
Als kleine Übungen kann man versuchen, BIT-Modell Algorithmen aufzuschreiben, die z.B. 'GE' oder 'Hello World' ausgeben - in Morse Code oder ASCII. Wer Lust hat, kann Ergebnise, Fragen oder Diskussionsbeiträge in das Kommentarfeld zum Blog eintragen.
Offenbar haben wir damit die BIT-Box verstanden. Gemeinerweise hat der Grosse Experimentator aber noch eine ganze Reihe von anderen BIT Boxen auf Lager. So finden wir jetzt eine Box in Blau vor, die im Wesentlichen so aussieht wie die BIT-Box. Allerdings hat sie ein weiteres Touch-Feld H, so dass wir links neben der Klappe jetzt die Berühr-Felder X und H finden. Und oben steht jetzt, Weiß auf Blau, "ZBIT".
Bevor wir uns aber daran machen, die ZBIT-Box zu analysieren, brauchen wir eine kleine Pause. Daher geht es im nächsten Teil weiter mit der ZBIT-Box.
Q2 Etwas ist anders! - Hello Qubit World
Schauen wir uns also als erstes einmal an, wie so ein Qubit-Algorithmus aussieht - auch ohne den schon zu verstehen.
Bekanntlich ist in der Welt der Informatiker, Programmierer, Hacker das erste, was man ausprobiert bei einem neuen System oder einer neuen Programmiersprache, ein "Hello World" zu erzeugen. Das allgemein anerkannte "Hello World" für Quantencomputer sieht allerdings schon etwas ungewöhnlich aus. Es liefert auch nicht die Grußformel, sondern ist nur so etwas wie das einfachste Qubit-Programm. (Natürlich kann man das Ergebnis daraus in der "normalen" Programmierwelt in ein "Hello World" umwandeln.) Wir werden sehen.
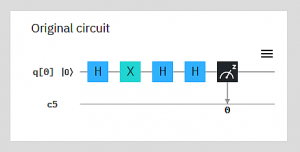
Und so sieht es aus, das "Hello World" der Qubit-Welt:
Sieht eher aus wie ein Ausschnitt aus einer Partitur moderner Musik? Der Vergleich ist gar nicht so unpassend. Dieser Ausschnitt "orchestriert" quasi die "Instrumente" eines Quantencomputers, die Qubits.
Am liebsten würde man das Bild sofort erklärt bekommen, aber das heben wir uns für später auf. Man sieht erst mal, ein Q-Algorithmus wird ganz anders dargestellt als üblich. Und dies ist eine einfache Möglichkeit einen Q-Algorithmus als Qubit-Programm grafisch zu beschreiben. (Das ist so ähnlich wie bei Scratch oder Roberta, wo man ein Programm visuell aus einzelnene Bausteinen zusammensetzen kann.) Natürlich kann man statt in der grafischen Form einen Q-Algorithmus auch in Worten beschreiben, wobei man aber sorgfältig mit der Sprache umgehen muss. Oder durch eine Programmiersprache, z.B. Python. Wir probieren das nachher mal.
Versuchen wir mal zu erraten, was die Grafik bedeutet, quasi als Partitur: Es gibt offenbar 2 Instrumente, q1 und q2. Die haben ihre eigene "Linie", auf denen etwas passiert. Klar, das sollen zwei Qubits sein - wobei wir erst in einem späteren Blog erklären, was Qubits sein sollen. Auf den Linien geschieht etwas, nacheinander, mit den jeweiligen Qubits. Was auch immer H macht, es macht es nur mit q1. Danach kommt etwas, dass offenbar q1 und q2 zusammen betrifft.
Am Ende jeder Qubit-Zeile steht eine Art Anzeige-Symbol, wie bei einem Messgerät, mit einem Pfeil nach unten auf die Doppel-Linie C. Tatsächlich, hier wird ein Qubit "gemessen". Und das Messergebnis wird an die C-Linie übertragen. Das "C" steht übrigens für "classical" - nein, nicht "klassische Musik", sondern "klassiches Bit", im Gegensatz zum Quanten-Bit oder Qubit. Danach kommt nichts mehr, es ist Schluß, das "Musikstück" zuende.
Was bedeuten die Zahlen unten auf der C-Linie? Das ist einfach zu erraten: die 2 besagt, dass C die "Messwerte" von 2 Qubits aufnimmt. Die 0, klar, steht für: "Hier kommt der Messwert von Qubit q0." Und die 1 für Messwert von q1 - falls es in einer größeren "Partitur" mal unübersichtlich werden sollte. Und da das C für "classical bit" steht, kann man schon schließen, dass die Messergebnisse herkömmliche Bits sind.
Jetzt wissen wir, was die Teile bedeuten, aber immer noch nicht, was der ganze Qubit-Schaltkreis macht (so nennt man das Gebilde in Anlehnung an herkömmliche elektronische Schaltkreise).
Das liegt daran, dass wir nicht wissen was die beiden blauen Symbole machen. Mal sehen, ob wir das auch noch verstehen können, z.B. indem wir den Hello Qubit World Algorithmus in normaler Sprache formulieren.
Aber jetzt ist es erst mal genug. Pause. Dann weiter lesen.
Cliff-Hanger - Stay tuned
Und hier geht's weiter.