Von Bernhard Thomas und Ulrich Trottenberg
Quanten-Computing wird in den Medien, aber auch in Vorträgen und in der Fachliteratur mit einer Reihe von Aussagen charakterisiert, die als Sprachkonstrukte ziemlich exotisch klingen – nach einer anderen Welt, in der logisch Unmögliches möglich scheint. Wir wollen uns einige dieser Sprachfiguren ansehen und überlegen, was dahinter steckt.
Unsere bisherigen Blog-Abschnitte über Qubit-Algorithmen sollten ausreichen, hier ein klares Verständnis zu schaffen. Hier die Übersicht über die Aussagen.
„Quanten können 0 und 1 gleichzeitig sein“
„Mit n Qubits kann man 2**n Zahlen gleichzeitig darstellen“
„Für N Zahlen benötigt ein Quanten-Computer nur log(N) Qubits“
„Ein Quanten-Computer kann mehrere Berechnungen gleichzeitig durchführen (Quanten-Parallelismus)“
„Was auf herkömmlichen Rechner Jahre dauert, kann ein Quanten-Rechner in Sekunden erledigen (Exponentielle Beschleunigung)“
„Quanten-Rechner werden herkömmlichen Rechnern überlegen sein (Quanten-Supremacy)“
„Jedes zusätzlich Qubit verdoppelt die Leistungsfähigkeit des Systems“
„Quanten können 0 und 1 gleichzeitig sein“
Dieser Satz und Abwandlungen davon ziehen sich durch die Quanten-Computing-Literatur wie ein Mantra des QC. Auch wenn er gelegentlich nur als Metapher gesehen wird, suggeriert dieser Satz in der öffentlichen Diskussion eine mystische Eigenschaft der Quanten, nicht zuletzt illustriert durch das Bild von Schrödingers Katze, die „gleichzeitig tot und lebendig“ ist.
Damit werden auch die informatischen Gegenstücke der Bits, die Qubits, charakterisiert. Im Gegensatz zu Bits, die nur „0 oder 1“ sein können, können Qubits „0 und 1 gleichzeitig“ sein.
Wie könnten wir das feststellen? Wir wissen, dass die Messung eines Qubits entweder 0 oder 1 ergeben kann, aber nicht beides. Wenn wir mehrfach messen, bekommen wir manchmal eine 0, manchmal eine 1 als Ergebnis, aber nie „gleichzeitig“. Was kann also gemeint sein – wenn es überhaupt einen Sinn ergibt.
Es gibt Varianten dieser „Gleichzeitig“-Sprachfigur, die etwas tiefergehend klingen: „Quanten können verschiedene Zustände gleichzeitig einnehmen“. Wir wissen, dass man Zustände von Systemen in Form von mathematisch eindeutigen Ausdrücken beschreiben kann – so auch Qubits und Qubit-Systeme. Ausgehend von einem Anfangszustand sahen wir, wie mittels Qubit-Operationen (oder Gates) ein Qubit-Zustand in einen nächsten überführt werden kann. Zu jedem Zeitpunkt ist der Zustand des Qubits daher eindeutig festgelegt. Wenn wir nicht unsere normale zweiwertige Logik (2 Wahrheitswerte: wahr, falsch – oder 0, 1) in Frage stellen, kann ein Qubit nicht zwei verschiedene Zustände gleichzeitig haben. Eine Zahl, ein mathematischer Ausdruck, der einben Zustand beschreibt, kann nicht gleichzeitig 0 und 1 sein: z = 0 = 1?
Manchmal findet man Texte, in denen das „Gleichzeitige“ durch die „Superpostion“ ergänzt wird: „Quanten können in einer Superosition von 0 und 1 gleichzeitig sein“. Wir wissen, was eine Superpostion ist. Z.B. ist 1/√2 (|0>+|1>), die Hadamard-Operation auf den Basiszustand |0>, eine Superpostion (oder mathematisch: Linearkombination) der Qubit-Zustände |0> und |1>. Wir haben Qubit-Zustände meist in Form von x-y-Koordinaten eines Punktes auf dem Einheitskreis beschrieben – im Beispiel also (1/√2,1/√2). Somit können wir korrekt formulieren: Ein Qubitzustand hat zwei Koordinaten. Aber was heißt dann „gleichzeitig“? Wenn jemand in Ingolstadt ist, befindet er sich z.B. auf der Strecke von München nach Nürnberg – aber ist er (möglicherweise) in München und Nürnberg „gleichzeitig“?
Wenn auch die Redewendung „… kann 0 und 1 gleichzeitig sein“ etwas Unsinniges suggeriert, können wir sie als solche akzeptieren, wenn man sie auf die Möglichkeit einer Superposition von zwei (Basis-)Zuständen eines Qubits zurückführt. Darin unterscheiden sich Qubits und Bits tatsächlich.
Und während ein Bit nur einen der beiden Zustände 0 oder 1 repräsentieren kann (siehe BIT-Box in Q3), kann ein Qubit einen Zustand aus einer unendlichen Menge von Superpositionszuständen annehmen. Wobei wir das „unendlich“ im Sinne aller Punkte auf dem Einheitskreis verstehen, ohne zu fragen, ob wirklich unendlich viele Superpositionen realisierbar sind (technisch und quantenmechanisch).
Eine elegante und gleichzeitig korrekte, einfache Erklärung finden wir im Glossar der IBM (Übersetzung DeepL):
Ein Qubit (ausgesprochen „kju-bit“ und kurz für Quantenbit) ist der physikalische Träger der Quanteninformation. Es ist die Quantenversion eines Bits, und sein Quantenzustand kann Werte von |0> , |1> oder die Linearkombination von beiden annehmen, was ein Phänomen ist, das als Superposition bekannt ist.
Mehr ist eigentlich nicht zu sagen.
„Mit n Qubits kann man 2**n Zahlen gleichzeitig darstellen“
Mit n Bits kann man zwar auch 2**n verschiedene Zahlen darstellen – gemeint sind Binärzahlen in Form von Bitketten – aber immer nur eine zu einem Zeitpunkt, z.B. im Speicher eines klassischen Computers.
Diese Aussage zusammen mit dem „Quantenparallelismus“ (s.u.) soll die überragende Leistungsfähigkeit von Quanten-Computern deutlich machen. Man liest auch: „Mit jedem weiteren Qubit verdoppelt sich die Kapazität“ und „Schon 300 Qubits können mehr Werte speichern, als das bekannte Universum Teilchen enthält“.
Nun ja, wie soll man das verstehen? Zunächst zu den beiden letzten Versionen des „Kapazitätssatzes“: Auch mit jedem weiteren Bit verdoppeln sich die möglichen Werte, die man speichern – und wieder lesen – kann. Immer einer zu einer Zeit (Schreib-Lese-Zyklus). Und mit 300 Bits kann man mehr als alle Teilchen des bekannten Universums abzählen, oder je eine Zahl zu einem Zeitpunkt im Bereich 0 bis 2**300-1 speichern. Bei Qubits liegt das Geheimnis offenbar wieder im „gleichzeitig“. Wieder nur eine Metapher?
Ein System von n Qubits, z.B. n=3, befindet sich zu einem Zeitpunkt in einem Zustand (von prinzipiell unendlich vielen), der eine Linearkombination (Superposition) von nunmehr 2**n Basiszuständen ist, also 8 bei n=3. In der ket-Schreibweise tritt jede n-lange Bitkette als ein Basiszustand auf, bei n=3 also |000>, |001>, |010>, |011>, |100>, |101>, |110>, |111>. Bei n = 300 sind es halt ……
Denken wir an Koordinatensysteme, wie z.B. in Q11, dann haben wir ein 8-dimensionales Koordinatensystem und jeder 3-Qubit-Zustand wird durch 8 Koordinaten beschrieben. „Gleichzeitig“ – für einen Punkt braucht man 8 Koordinaten „gleichzeitig“.
Kann man in einer Superposition von 2**n Basiszuständen das gleichzeitige Speichern von 2**n Zahlen sehen? Nehmen wir eine gleichmäßige (uniforme) Superposition, d.h. alle Basiszustände kommen mit dem gleichen Koeffizienten vor. Bei n=3 also mit 1/√8.
Speichern nützt nur dann etwas, wenn man mit dem Gespeicherten etwas anfangen kann, z.B. weiter verarbeiten mittels Qubit-Operationen oder Lesen, d.h. Messen. Beim Weiterverabeiten zu einem neuen Zustand können tatsächlich alle Komponenten der Linearkombination in einer Operation berücksichtigt werden (Quantenparallelismus, s.u.). Beim Messen (gegen die Basiszustände) erhält man eine Häufigkeitsverteilung über alle Bitketten, die als Basiszustände in der aktuellen Superposition vertreten sind. Sind einige nicht vertreten, tauschen sie, bis auf Quantenfehler, auch nicht im Messergebnis auf.
Aber was machen wir damit? Welche Information ziehen wir daraus? Dass 2**n Bitketten beim Messen auftreten können, wussten wir schon vorher. Wir „lesen“ also nichts Neues. Wenn wir 2**300 Teilchen mit unterschiedlichen Bitketten versehen wollten, konnten wir das auch schon ohne Quanten-Computer (QC).
Wo liegt also die Information, die wir durch die Quanten-Berechnung gewonnen haben? Wohl in der gemessenen Häufigkeitsverteilung:
- Wir schauen nur auf „vorhanden“ und „nicht vorhanden“ von gemessenen Bitketten. Eine häufige Form der Interpretation von QC-Ergebnissen, z.B. beim Herausfinden eines Orakels, wie im Bernstein-Vazirani Problem oder dem von Deutsch-Josza. Man kann sich das so vorstellen: Der Qubit-Algorithmus „rechnet“ mit den 2**n Basiszuständen des n-Qubit Systems, der Ergebnis-Zustand enthält aber in nur einen Basiszustand, der dann bei der Messung eine ziemlich eindeutige Bitkette liefert. Eine solche Methode ist auch die sogenannte Amplituden-Verstärkung (amplitude amplification). Zum Auffinden einer bestimmten Bitkette beginnt man mit einer uniformen Superposition und verändert diesen Zustand Schritt für Schritt so, dass die Amplitude des Basiszustands mit der gesuchten Bitkette zunehmend „größer“ wird. Die Iteration wird beendet, wenn man nahe genug an der gesuchten Bitkette ist, d.h. wenn beim Messen diese Bitkette eine überragende Wahrscheinlichkeit erreicht. Das Verfahren wird auch Grover-Iteration genannt.
- Uns interessiert ein „numerisches“ Ergebnis, z.B. eine Zahl oder eine Reihe von Zahlen (Vektor), die sich bei der Messung am Ende der Rechnung als Häufigkeiten bestimmter Bitketten ergeben. Als „numerisches“ Ergebnis nimmt man dann die Liste dieser Häufigkeiten. Hier stoßen wir aber auf verschiedene Probleme. Eines davon ist, dass ein echter QC die Häufigkeiten nicht exakt misst. Um halbwegs brauchbare Werte abzuleiten, müssen wir das QC Programm wiederholt durchlaufen lassen. Wie oft? Für n=3 kann man das ja einmal ausprobieren mit dem IBM QC. Wie oft bei n=50 oder n=300?
„Für N Zahlen benötigt ein Quanten-Computer nur log(N) Qubits“
Dies ist eine Variante der vorigen Aussage und besagt: „Während man auf herkömmlichen Computern für N Zahlen auch N Speicherplätze benötigt, braucht ein Quanten-Computer nur log(N) Qubits“. Man hat also, umgekehrt gesehen, einen exponentiellen Effekt. Und damit ist ein Quanten-Computer exponentiell leistungsfähiger als ein herkömmlicher. Wie auch immer das gemeint ist, es läuft darauf hinaus, dass man eine Überlagerung der N Basiszustände eines „log(N) großen“ Qubit-Systems herstellt, bei der die Koeffizienten (auch Amplituden genannt) gerade die gewünschten N Zahlen sind. Wenn man also weiß, wie, kann man einen solchen Superpositionszustand als „Input“ herstellen, und einen Qubit-Algorithmus damit weiterrechnen lassen. Das ist das sog. Amplituden-Verfahren oder auch Amplituden Encoding.
Aber halt! Die N Amplituden müssen ja in der Summe der Quadrate 1 ergeben. Schränkt das nicht die freie Wählbarkeit der N Zahlen ein? Nicht wirklich – man muss nur vorher jede Zahl durch die Summe aller Quadrate teilen, genauer, durch die Quadratwurzel dieser Summe. Damit kann man dann „Quanten-Rechnen“. Allerdings tritt bei der Ergebnis-Festellung wieder das Problem aus 2. auf.
Um die N Zahlen als Input verwenden zu können, muss man zu Beginn des Qubit-Algorithmus geeignete Qubit-Operationen (Gates) ausführen, so dass sie in einer Superposition zu Koeffizienten von Basiszuständen werden. Das kann trotz „Quantenparallelität“ aufwendig sein. Hier ein Beispiel:
Angenommen, wir wollen die 4 Zahlen 1.0, 1.0, √2 = 1.414, 2.0 als Input in Form von Amplituden für ein 2-Qubit-System bereitstellen (N=4, n=2). Die Summe der Quandrate ist 1.0+1.0+2.0+4.0 = 8.0. Die Wurzel daraus ist √8. Dadurch müssen wir die 4 Zahlen teilen, damit diese eine gültige 2-Qubit Superposition ermöglichen: 1/√8, 1/√8, 1/√4, 1/√2. Es ist damit z.B. der Zustand 1/√8 |00> + 1/√8 |01> + 1/√4 |10> + 1/√2 |11> durch einen Qubit-Circuit herstellbar. Wie geht das? Hier ist eine Lösung:


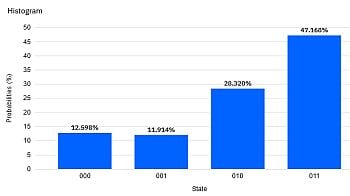
Das „Fine-Tuning“ der Amplituden erfolgt hier mittels Drehungen (Ry). Der resultierende Zustand ist verschränkt, d.h. er kann nicht als Kombination der einzelnen Qubits hergestellt werden. Das kann man nach der Methode in Q9 nachprüfen. (Ergebnis eines Simulatorlaufs mit 1024 shots.)
„Ein Quanten-Computer kann mehrere Berechnungen gleichzeitig durchführen“
Diese Aussage wird häufig als Verdeutlichung des sog. Quanten-Parallelismus verwendet. Auch hier wird wieder das Mantra-Wort „gleichzeitig“ verwendet, dieses Mal aber in einer sinnvollen Bedeutung, nämlich im Gegensatz zu „nacheinander“ (sequentiell). Natürlich können auch herkömmliche Computer heutzutage mehrere Berechnungen zeitlich parallel ausführen. Der Unterschied ist aber technisch fundamental: Herkömmliche Parallelrechner (z.B. MIMD-Architekturen) führen mehrere, durchaus auch verschiedene, Computerbefehle (Instructions) zur gleichen Zeit aus und verwenden dabei u.U. unterschiedliche Daten als Input.
Quanten-Computer führen zu einem Zeitpunkt einen Befehl (in Form von Gates) auf einer Datenstruktur aus. Die Datenstruktur ist der aktuelle Zustand eines n-Qubit-Systems, also meist eine Superposition oder gar eine Verschränkung. Der Zustand eines n-Qubit-Systems kann aber, wie wir zuvor gesehen haben, bis zu N=2**n Zahlen (in Form von Amplituden) repräsentieren. Indem der Qubit-Befehl auf den Zustand wirkt, wirkt er simultan auf alle Basiszustände, die in der Superposition vorkommen. Als Ergebnis können sich damit simultan alle Amplituden der Basiszustände verändern. Bingo!
Mathematisch gesehen ist das überhaupt nichts Ungewöhnliches. Eine Matrix A „wirkt“ bei Multiplikation mit einem Vektor x auf alle seine Komponenten „gleichzeitig“: y= Ax (Lineare Algebra). Wird ein Punkt (x,y) mittels einer Funktion F verschoben, dann werden alle Koordinaten „gleichzeitig“ verschoben: (u,v) = F(x.y). Und auch die Qubit-Operatoren (Gates) können mathematisch als Matrizen dargestellt und verwendet werden. Wenn es allerdings ans praktische Rechnen geht, etwa mit einem Algorithmus, der die Matrixmultiplikation explizit durchführt, dann geht es klassisch (auf einem herkömmlichen Rechner) wieder nur Schritt für Schritt: die Operation wird in viele Einzelschritte zerlegt, die nacheinander ausgeführt werden. Hier unterscheiden sich klassische und Quanten-Computer tatsächlich fundamental. Quanten-Computer, wie die von IBM, sind technisch so aufgebaut, dass sie eine komplette Superposition in einem, statt in vielen Schritten verarbeiten können.
Wie man sich das vorstellen kann, zeigen wir an einem einfachen Beispiel: Das exklusive Oder (XOR) von zwei Bits entspricht der einfachen Bit-Addition bis auf die Operation „1+1“, die 0 ergibt statt 2. (Dafür verwendet man auch das Symbol ⊕ statt +). Wir können die Bit-weise XOR-Berechnung auch als Qubit-Circuit durchführen. Das ergibt die 4 Auswertungen in der Abbildung, wobei jeweils q0 und q1 auf Zustand 0 bzw. 1 gesetzt werden und das Ergebnis den neuen Zustand von q1 ergibt.
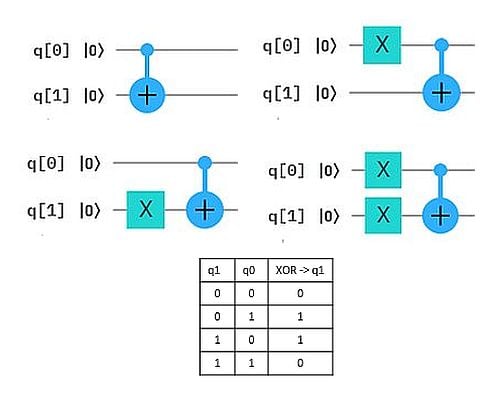
Quanten-Parallelismus ermöglicht aber Superpositionen statt einzelner Basiszustände als Input zu präparieren, typischerweise mit dem H-Gate (Hadamard-Gate). Damit muss die Berechnung nur einmal ausgeführt werden und wir erhalten alle 4 Ergebnisse auf einmal.
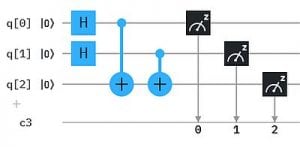
Um die Ergebnisse einfacher „lesen“ zu können, haben wir hier das XOR Ergebnis auf ein drittes Qubit q2 übertragen. So erhalten wir als Messergebnis genau die obige XOR Tabelle mit XOR -> q2 : 000, 101, 110, 011 (q2 steht hier wieder jeweils ganz links in der Bitkette).
„Was auf herkömmlichen Rechnern Jahre dauert, kann ein Quanten-Rechner in Sekunden erledigen“
Als Begründung liest man dabei oft, dass Quantenrechner „exponentiell schneller“ rechnen können als herkommliche. Was bedeutet das?
Das heißt zum Beispiel folgendes: Wenn wenn wir zwei Methoden haben, die eine Aufgabe lösen, etwa eine Berechnung durchführen oder ein „Geheimnis“ (Q15) zu finden, und die eine Methode benötigt N Zeiteinheiten oder Rechenschritte, die andere aber nur log(N) viele, dann stellt die zweite Methode eine exponentielle Verbesserung – oder Beschleunigung – gegenüber der ersten dar. (Denn, für k=log(N) ist N=exp(k).)
Es gibt eine ganze Reihe von solchen „Beschleunigungsbeziehungen“ zwischen Methoden zur Lösung gleicher Aufgaben. Der Grover Qubit-Algorithmus benötigt nur etwa √N Schritte gegenüber N Schritten bei der klassischen Methode. Hier haben wir also eine quadratische Beschleunigung. In Q15 hatten wir das am Beispiel des Bernstein-Vazirani-Algorithmus diskutiert.
Solche Beschleunigungen gibt es von je her auch im klassischen Computing als Effekt einer algorithmischen Verbesserung. So gibt es z.B. unterschiedliche Sortier-Algorithmen, die sich bezüglich ihres Rechenaufwands erheblich unterscheiden, oder auch Verfahren zur numerischen Simulation, bei denen sogenannte Mehrgitterverfahren große Beschleunigungsraten bringen.
Der tatsächliche Beschleunigungseffekt des Quanten-Computing gegenüber herkömmlichen Bit-Computing beruht auf einer Kombination von zwei Dingen: dem Quanten-Parallelismus der Hardware (s. voriger Abschnitt) und dem Algorithmus, der für Qubits konstruiert werden kann.
Ein Rechenbeispiel: Hätte man eine (hypothetische) Aufgabe, die auf einem gewöhnlichen Rechner mit dem schnellsten Algorithmus 10 Jahre dauern würde, dann würde eine exponentielle Beschleunigung auf einen Zeitaufwand von rund 20 Sekunden führen: log(10*360*24*60*60) = log(311040000) = 19,56. Diese Zahlen sind allerdings eher fiktiv, da wie keine konkrete Aufgabe vor Augen haben und Wiederholungen und anderen „Overhead“ nicht berücksichtigen. Aber es zeigt, wie sich die Größenordnung ändern.
Hätten wir also eine Aufgabe, die herkömmlich Jahre dauern würde, und hätten wir dazu ein Quanten-Computer, der sie alternativ mit exponentieller Beschleunigung löst, könnten wir die Aussage so akzeptieren. Allerdings gibt es noch nicht viele Algorithmen für Quanten-Computer, die in dieser Form praktische verwendbar sind. Was nicht zuletzt auch an der Größe und „Sensibilität“ heutiger QC liegt.
Ein relevantes Beispiel, das immer wieder als „Gefahr durch Quanten-Computer“ zitiert wird, ist das Verfahren von Shor, mit dem man einen wichtigen Schritt beim „Knacken“ von besten heutigen Verschlüsselungsverfahren in akzeptabler Zeit durchführen kann. Um das zu verstehen, braucht es aber schon mehr Einsicht in die zugrunde liegende Mathematik. Daher wird hier meist nur der (befürchtete) Effekt zitiert und auf Verständnis verzichtet.
„Quanten-Rechner werden herkömmlichen Rechnern überlegen sein“
Man spricht auch generell von Quanten-Überlegenheit (Quantum Supremacy). Trotz der beängstigent klingenden Bezeichnung handelt es sich hier um eine unspektakuläre Sache. Es bedeutet lediglich das Ereignis, dass es eine Berechnung gibt, die ein Quanten-Computer schneller als jeder herkömmliche Supercomputer durchführen kann. Dabei ist es erst einmal egal, ob diese Berechnung einen Sinn macht oder praktische Bedeutung hat. Wie man kürzlich lesen konnte, hat man (mit einem QC von Google) bereits eine solche Berechnung durchführen können, d.h. der Meilenstein Quantum Supremacy ist schon erreicht.
„Jedes zusätzlich Qubit verdoppelt die Leistungsfähigkeit des Systems“
Hier bleibt einerseits unklar, was mit Leistungsfähigkeit gemeint ist – Rechenleistung, Speicherleistung, Leistung eines Algorithmus, der ein Qubit mehr zur Verfügung hat? Auch wenn wir einen Bit-Speicher (Register) um ein Bit erweitern, also von n auf n+1 Bits, können wir damit 2**(n+1) = 2*2**n Werte speichern bzw. mehr oder längere Befehle ausführen. So hatte sich auch die Prozessorarchitektur von früheren 32 Bit auf 64 Bit bei herkömmlichen Computern verändert und dabei prinzipiell eine 32-fache Verdoppelung der Leistung ermöglicht.
Was macht nun ein Qubit mehr aus bei einem Quanten-Computer? Zum einen gibt es dann doppelt so viele Basiszustände. Z.B. von 8 bei einem 3-Qubit System auf 16 bei 4 Qubits. In Superposition können damit 16 statt nur 8 Koeffizienten (Amplituden) einen Zustand bestimmen. Diese Verdoppelung ist analog der Situation bei Bits und wir hatten das schon oben bei N vs log(N) erklärt.
Zum anderen wissen wir, dass – ganz ander als beim Bit-Computing – verschränkte Zustände eine wichtige Rolle im Qubit-Computing spielen. Man kann sich also fragen, was bringt ein zusätzliches Qubit für die möglichen Verschränkungen, oder allgemein für die möglichen „Konfigurationen“ von Superpositionen. Anders ausgedrückt: wieviel mehr Möglichkeiten gibt es für Zustände, in denen nur ein Basiszustand vertreten ist, oder zwei, oder drei usw. – unabhängig von den Werten der Amplituden. Diese Zahl wächst offenbar kombinatorisch. Für n=2 sind die „Muster“ noch überschaubar: 4 mal |x>, 6 mal |x>+|y>, 3 mal |x>+|y>+|z> und 1 mal |x>+|y>+|z>+|v>, wenn |x>,|y>,|z>,|v> die Basiszustände |00>, |01>,|10>,|11> durchlaufen.
In Q13 (Superdichte Codierung) haben wir einen anderen Verdopplungseffekt gesehen: die Kapazität, Bitketten in GHZ-verschränkten Qubits zu „speichern“ bzw. zu übertragen. Hier brachte jedes weitere Qubit in einer solchen Verschränkung eine Verdoppelung der Anzahl übertragbarer Bitketten.
Zuletzt eine Anmerkung: Bei „Was man so liest“ fragt man sich leicht, wo man das gelesen hat. Die konkreten Aussagen in den Überschriften sind keine echten Zitate, obwohl sie so oder in Variationen der Wortwahl tatsächlich vorkommen. Wir wollen hier aber kein „Bashing“ anzetteln, sondern nur kostruktiv klären, was dahinter steckt oder wo man leicht fehlgeleitet wird. Daher verzichten wir auf Quellenangaben.
