Bernhard Thomas, Ulrich Trottenberg
Interscience-Akademie für Algorithmik (ISAfA)
Stand: 29.08.22
Update: 23.08.23
In seinem Blogbeitrag vom 19. Februar 2022 beschreibt Ulrich Trottenberg eine fundamentale Veränderung in der Wahrnehmung von Algorithmen. Mit der verbreiteten Anwendung von Algorithmen, die der Künstlichen Intelligenz zugerechnet werden, sehen wir zunehmend Algorithmen, die nicht in herkömmlicher Weise feste Abläufe (Programme) implementieren, sondern sich selbst modifizieren. Trottenberg beschreibt dies in Zusammenhang mit Maschinellem Lernen als einen Wandel in der Algorithmik “vom programmierten zum trainierten Algorithmus” und wirft dazu eine ganze Reihe von Fragen auf, die aus dieser Unbestimmtheit der Selbstmodifikation resultieren – von der prinzipiellen Verstehbarkeit oder Nachvollziehbarkeit der algorithmischen Abläufe bis zu Fragen der Verantwortung und Kontrolle für die Ergebnisse.
Grundsätzlich ist in der Softwareentwicklung zwar allgemein bekannt und akzeptiert, dass Algorithmen (bzw. Programme), die eine gewisse Anzahl an Statements, Verzweigungen oder Modulen überschreiten, nicht mehr vollständig verstanden und auf Fehlerfreiheit geprüft werden können. Ein Algorithmus, der sein Verhalten im Ablauf modifiziert hat, entzieht sich dagegen zusätzlich einer systematischen a priori Prüfung – auch wenn die Implementierung primär einer klassischen Softwareentwicklung folgt. Ein “trainierter Algorithmus” ist in seiner Grundstruktur zwar klassisch, sein Verhalten und seine Leistung ist dagegen nicht Ergebnis eines Programmierer-Eingriffs, sondern Ergebnis einer Selbstmodifikation, etwa eines sog. „Trainings“ – wie auch immer sich dieses gestaltet. Allerdings ist die Fähigkeit und Art der Selbstmodifikation bis heute im Grunde immer noch die Leistung eines Programmierers oder Ingenieurs (m/w/d).
Der “Zustand” eines Algorithmus
Wie Trottenberg schreibt, sind “Algorithmen in ihrem Kern mathematische Konstrukte”. Man kann sie mathematisch als sog. Endliche Automaten beschreiben. Also als ein Konstrukt (oder Denkschema), das durch die drei Begriffe Input, Zustand und Output und zwei “Überführungsfunktionen” beschrieben wird. “Überführung” deshalb, weil die eine einen Input in Abhängigkeit vom Zustand in einen Output überführt, und die andere einen Zustand in Abhängigkeit vom Input in einen neuen Zustand überführt. Man kann sich dies leicht an diesem Schema verdeutlichen:
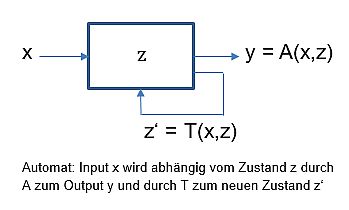
Üblicherweise sieht man in klassischen Algorithmen, oder deren Programmen, nur eine Input-Output-Beziehung, wie das old-school IT-Mantra E-V-A (Eingabe – Verarbeitung – Ausgabe) andeutet. Um das Paradigma des “Algorithmenwandels” zu verdeutlichen, muss man den “Zustand” eines Algorithmus – im Sinne eines Endlichen Automaten 1 – berücksichtigen.
Während die Begriffe Input und Output unmittelbar verständlich sind, muss man dagegen noch bestimmen, was der Zustand eines Algorithmus (oder des Programms) ist: Als Zustand eines Algorithmus kann man die Gesamtheit aller seiner Parameter und seiner Anweisungen (Statements, Befehle, Schritte) verstehen.
Die Berechnung eines Outputs für einen gegebenen Input hängt offensichtlich vom Zustand ab. Das ist nichts Neues. Die gleichzeitige Zustandsveränderung ist dagegen eine eher neue Sichtweise. Ein Algorithmus kann – in Abhängigkeit vom Input und dem aktuellen Zustand – seinen Zustand verändern, also z.B. seine Parameter und/oder Statements. Damit ändert sich das Verhalten des Algorithmus, d.h. seine Output-Antwort auf einen Input, ohne einen Eingriff von außen (etwa dem Programmierer). Das bedeutet u.a., dass der gleiche Input einen unterschiedlichen Output liefern kann – aufgrund der Tatsache, dass sich der Zustand verändert hat.
Das Foto einer Birne als Input kann als Output eines Klassifikationsalgorithmus die Kennzeichnung “Banane” ergeben, nach Änderung des algorithmischen Zustands (Selbstmodifikation) aber als “Birne” klassifiziert werden.
Der Zustand eine Algorithmus kann einfacher, überschaubarer Struktur sein – wie in dem Beispiel unten – oder hochkomplex und kaum mehr verstehbar. Tiefe neuronale Netze, etwa zur Bilderkennung, haben oft viele Millionen Parameter – oder viele Milliarden, wie bei ChatGPT – und komplexe Strukturen mit einer großen Zahl von mathematischen Anweisungen. Wissenschaftliche und kommerzielle Software hat oft Millionen “lines of code” (Anweisungen).
Zustandsänderungen im Verlaufe eines Algorithmus betreffen überwiegend den Parameter-Teil des algorithmischen Zustands (Adaptive Verfahren, Lernende Algorithmen). Selten werden heute auch die Anweisungen (Programmbefehle) verändert. So etwa bei Genetischen oder Evolutionären Algorithmen, die (als Programme) ihren eigenen Code verändern können, um sich an bestimmte Anforderungen besser anzupassen. Bei “Algorithmenwandel” denkt man diese Fälle nur am Rande mit.
Lernende Algorithmen
Das Birnen-Beispiel ist typisch für einen lernenden, oder lernfähigen, Algorithmus. Lernende Algorithmen (Machine Learning) sind dadurch charakterisiert, dass sie in ihrem Ablauf von einem Zustand des “Etwas-Nicht-Könnens” in einen Zustand des “Könnens” übergehen. Diesen Vorgang bezeichnet man bildlich auch als “Training”. Im Detail bedeutet das, dass der interne Zustand des Automaten (seine Parameter) mit dem Output rückgekoppelt wird – genauer, durch die Abweichung von einer Vorgabe für den Output angepasst (trainiert) wird.
Das einfache Automatenschema erweitert sich damit durch eine Rückkopplung des Outputs – hier als Fehlerwert f gegenüber dem Soll-Wert y* (Thermostat-Prinzip).
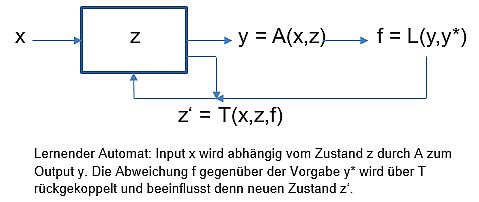
Das Besondere am Algorithmenwandel ist daher, dass das Verhalten eines Algorithmus durch Training verändert wird, statt durch explizites Programmieren. Allenfalls wird vorgegeben, was “Können” bedeutet, was also “gekonnt” werden soll – und das in einer algorithmen-tauglichen Formulierung.
Dies ist zu unterscheiden von Algorithmen, die per se so entwickelt wurden, dass sie “etwas können”. Wir demonstrieren das weiter unten an einer schlichten überschaubaren Aufgabenstellung: Lernen, gerade und ungerade Zahlen zu unterscheiden.
Es ist natürlich überhaupt kein Problem, einen Algorithmus zu entwerfen, der gerade und ungerade Zahlen unterscheiden kann! Die meisten Algorithmen wurden und werden entworfen, etwas zu können, z.B. Wetterberechnung, Flugbahnen, Verschlüsselung. Dies zum Unterschied dazu, diese Fähigkeit zu lernen – also im Sinne des Algorithmenwandels durch Zustandsänderung zu erwerben. 2
Lernende Algorithmen bilden eine der Säulen, wenn nicht die wichtigste, der Künstlichen Intelligenz, ein heute vielfach verwendeter Begriff, den wir an dieser Stelle undiskutiert lassen wollen.
Ein überschaubares Modell-Problem
Zu unterscheiden, ob eine Zahl (dem Wert nach) gerade oder ungerade ist, ist – auch algorithmisch – sehr einfach.
Einige einfache Beispiele für Algorithmen, die das können:
- Teile x durch 2 mit Rest y. Gerade: y=0, ungerade y=1
- Wandle x ohne Vorzeichen in eine Binärzahl. y letzte Binärstelle
- Subtrahiere 2 von x (ohne Vorzeichen), solange bis x=1 oder 0
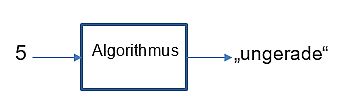
Hier zwei weitere, etwas ungewöhnliche Beispiele:
- x -> z = (-1)**x -> y = sign(z)
- x -> z = sin(pi/2*x)**2 -> y = sign(z-0.5)
Geben wir den Algorithmen beispielsweise die Inputs (x) 251 bzw. 2046, so errechnen sie als Output (y) -1 bzw. 1. Dabei steht 1 für gerade, und -1 für ungerade, wie wir einfach mit x=1 und x=2 nachrechnen können.
Warum diese beiden besonderen Beispiele? Hier lässt sich der Zustand des Algorithmus leicht identifizieren. Er ist jeweils durch einen Parameter und zwei Anweisungen bestimmt
Algorithmus 1:
[Parameter: a=-1 | Statements: v = a**x; y=sign(v)]
Algorithmus 2:
[Parameter: alpha=pi/2 | Statements: v = sin(alpha*x)**2; y = sign(v-0.5)]
In diesem Zustand berechnen die Algorithmen das Ergebnis direkt; d.h. sie können gerade / ungerade unterscheiden.
Ein lernender Algorithmus unterscheidet sich davon dadurch, dass er die Unterscheidung nicht per se errechnen können muss, sondern sich in einen Zustand bringen kann, in dem er das kann. Es ist klar, dass ein in diesem Sinne lernender Algorithmus etwas komplexer ist. Er muss ja zusätzlich zur Berechnung den Ablauf einer zielgerichteten Anpassung seines Zustands – hier des Parameterwertes – umfassen. Man bekommt die “Lernfähigkeit” des Algorithmus also nicht nebenbei – jedenfalls solange, wie es keine Algorithmen gibt, die ihre Statements zielgerichtet selbst-modifzierend ändern.
“Trainierte Algorithmen” im Sinne des Algorithmenwandels entstehen also bis auf weiteres durch die (selbstständige) Entwicklung ihrer Zustände bzw. ihres Verhaltens per Parameteranpassungen. Die Trainierbarkeit ist allerdings vorab im Algorithmus vorzusehen bzw. zu programmieren. Wir zeigen das am Beispiel des Algorithmus 1:
Algorithmus 1:
Hat der Parameter a anfangs einen beliebigen Wert wie z.B. a=1.5, so kann der Algorithmus offensichtlich keine ungeraden Zahlen erkennen. (Beispiel: x = 5 als Input führt zu y = 1; 5 wird damit als gerade erkannt, was offensichtlich falsch ist 3
Mit einer geeigneten „Lernkomponente“ kann der Algorithmus sich darauf trainieren, die 5 und andere Zahlen richtig zu klassifizieren. Der Algorithmus modifiziert dazu den Zustandsparameter a durch Korrekturen, die er aus den Fehlern berechnet, die er im aktuellen Zustand (i.e. Parameterwert) für einige vorgegebene Beispiele (Trainingsdaten) macht. 4. Wenn er nach einer Anzahl wiederholter Korrekturen z.B. den Parameterwert a = -1 erreicht, hat er “gelernt”, gerade und ungerade Zahlen zu unterscheiden. 5
Die Box zeigt beispielhaft Trainingsdaten, den Trainingsvorgang (Iterationen) und das Ergebnis anhand von einigen Testdaten. 6 7
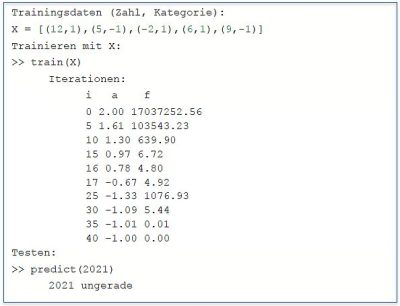
Das Verfahren der Modifizierung ist “Numerische Mathematik” – und nicht immer trivial. Im Beispielalgorithmus für die Gerade/Ungerade-Erkennung muss nur ein Parameter in einer einfachen Funktion “trainiert” werden; in vielen Anwendungsfällen von z.B. tiefen, strukturierten Neuronalen Netzen sind es aber schnell mal Millionen in einer komplexen Hierarchie von Funktionen. Weit davon entfernt, dass KI-Algorithmen solche Verfahren selbständig entwickeln, ist es nach wie vor Gegenstand intensiver Forschung, wie das am besten geht.
Der Algorithmus 2, der auch nur einen Parameter (alpha) enthält, ist interessanterweise in diesem Sinne nicht lernfähig. Er lässt sich nicht durch Training in den Zustand bringen, in dem er gerade / ungerade Zahlen unterscheiden kann (alpha = pi/2). Warum das so ist, ist an anderer Stelle erklärt (s. „Six not so easy pieces for AI“ im ISAfA Blog) 8
Algorithmenwandel
Der Algorithmenwandel ist demnach durch zwei Aspekte charakterisiert:
- Das Verhalten oder die Leistung eines Algorithmus ist nicht direktes Ergebnis einer Intervention des Designers.
- Die Entwicklung zu dieser Leistung geschieht über die Entwicklung von Zustandsparametern, deren Bedeutung – insbesondere bei großer Parameteranzahl – nicht unbedingt verstanden wird.
Da die Rolle und der Veränderungsvorgang der Parameter expliziter Bestandteil des zugrunde liegenden Algorithmus sein müssen, ist theoretisch beides ableitbar und erklärbar – praktisch aber nur schwer und in seltenen, einfachen Fällen machbar. Die Forschungsdisziplin “Erklärbare KI” (XAI) befasst sich mit diesem Problem.
Der “Wandel” ist auch ein Wandel in unserer Wahrnehmung dieser selbst-modifzierenden Algorithmen. Wir akzeptieren, dass Algorithmen ohne unser explizites Zutun ihr Verhalten ändern, sind dabei aber unsicher, weil oder solange wir nicht verstehen, was da passiert.
Iterationen, also der wiederholte Ablauf von Algorithmus-Schritten, sind natürlich auch Bestandteil herkömmlicher, “programmierter” Algorithmen, etwa in wissenschaftlichen Berechnungen (Wetter, Flugbahnen etc.). Hierbei werden aber im Wesentlichen Berechnungsgrößen iteriert (etwa Druck, Temperatur, Windströmung). Parameter treten dabei als Modellparameter auf (etwa in der Diskretisierung der Geographie bei einem Wettermodell). Die Parameter von KI -Algorithmen, insbesondere bei Machine Learning Verfahren, sind dagegen Zustandsparamter des Algorithmus, die im Zuge des Trainings iteriert werden.
Fußnoten
1 Übrigens ist der englische Begriff für den Endlichen Automaten “Finite State Machine”, was umgekehrt auch noch einmal den Blick auf die Bedeutung von „Machine Learning“ lenkt. Formal sind die hier besprochenen Algorithmen nicht wirklich „endliche“ Automaten: ihre Zustände bestehen zwar immer aus endlich vielen Komponenten, die aber meist kontinuierliche Werte annehmen können. Einen einfachen E-V-A Automaten, der also lediglich einen Input in einen Output überführt, bezeichnet man auch als Moore-Automat. Bei einem Mealy-Automaten hängt der Output auch vom Zustand ab.
2 Man kann sich natürlich fragen: Wozu brauche ich einen Algorithmus, der etwas lernen kann, wenn es einen Algorithmus gibt, der das schon kann? Die Antwort ist einfach: Es gibt Problemstellungen, die man mit einem lernenden Verfahren durch Training lösen kann, für die es aber schwer fällt, diese Lösung direkt zu programmieren. (Bildanalysen, Textanalysen, Sentiment-Analysen, Sprach-Synthese u.v.m).
Nebenbei – die umgekehrte Frage ist auch interessant und durchaus aktuell: Warum muss ich einen Algorithmus explizit für die Lösung eines Problems entwickeln, wenn ein lernender Algorithmus diese Lösung erlernen kann?
3 Der Spruch “Fünf gerade sein lassen” hat aber wohl nichts mit KI zu tun.
4 Wir unterstellen hier stillschweigend, dass die Vorgabebeispiele als Input sowohl die Zahl als auch die Gerade/Ungerade-Klassifizierung in Form von +1 bzw. -1 enthalten. Diese Methode nennt man – aus heute unerfindlichen Gründen – “überwachtes Lernen” (supervised learning). “Überwacht” wird der Lernvorgang faktisch durch die Trainingsbeispiele, in Analogie zur Überwachung durch einen “Trainer” oder Lehrer.
5 In einem Programmlauf wird der Wert -1 nicht wirklich erreicht, sondern nur angenähert, etwa -0.999. Prinzipiell reicht dem Algorithmus aber auch ein solcher Wert, um gerade / ungerade zu unterscheiden. Wie in vielen anderen Fällen auch, gibt es durchaus verschiedene trainierte Zustände, mit denen der Algorithmus die gewünschte Leistung erbringen kann. Meist nicht “mathematisch perfekt”, aber für alle praktischen Fälle korrekt.
6 Das Verfahren zur Parametermodifkation lassen wir hier weg. Es ist i.w. die bekannte Newton-Iteration, naiv angewandt auf eine Fehlerfunktion (mean square error).
7 Tatsächlich kommt das naive Verfahren mit wenigen Trainingsdaten aus – je weniger, desto besser. Es reicht bereits das Training mit X=[(1,-1)].
8 Zahlen dem Wert nach in gerade und ungerade Zahlen klassifizieren zu lernen ist nicht gerade eine einfache ML Aufgabe. Einfacher wird das Lernproblem, wenn die Zahlen als Ziffernketten gesehen werden. Ein Beispiel findet man in diesem Blogbeitrag.
