KI im Informatikunterricht
Dieser Beitrag kann als Grundlage für die Einführung des Themas „Künstliche Intelligenz“ im Schulunterricht eingesetzt werden. Er illustriert „Maschinelles Lernen“ anhand einer für die Schüler* einfach verständlichen Aufgabe mittels einer Data Analytics Methode: Naive-Bayes. Die Aufgabe kann mit „Papier und Bleistift“ durchgeführt werden. Die Voraussetzungen beschränken sich auf Erstellen von Tabellen, Auszählen von Häufigkeiten und Berechnung von relativen Häufigkeiten.
Die Blogserie „Six not so easy pieces for AI” (Sechs nicht so einfache Aufgaben für AI) begann in 2019 mit der einfachen Fragestellung, ob AI in der Lage ist, eine der einfachsten „intellektuellen“ Leistungen zu erbringen, nämlich zu lernen, ob eine Zahl gerade oder ungerade ist. (Siehe hier.)
Abstrakte Fragestellung – Allgemeines Schema
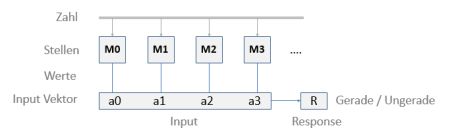
Hier bedeuten die einzelnen Attribute des Input-Vektors die Dezimalstellen einer ganzen Zahl, beginnend bei den „Einern“ ganz rechts. Der Wertebereich (Kategorien-Labels) ist jeweils 0,1,…,9. Die Response im Supervised Learning gibt jeweils an, ob die Zahl gerade oder ungerade ist. Die entsprechenden Klassen sind 0 (für Gerade) und 1 (für Ungerade). Im trainierten Zustand gibt R die „Vorhersage“ für eine Testzahl.
Es ist wichtig zu bedenken, dass ein „lernendes KI-System“ hier kein Konzept von Zahlen, Dezimalstellen und deren Bedeutung innerhalb einer Zahl (z.B. Einer, Zehner etc.) hat. Die Inputs sind für das System nichts weiter als eine Liste von Ziffern.
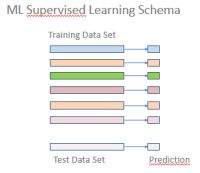
Das Training-Szenario
Als Training-Daten wird eine Anzahl von ganzen positiven Zahlen in Form einer Liste der einzelnen Dezimalstellen samt der richtigen Klassifikation in gerade / ungerade vorgegeben.
Als Testdaten werden einzelne Zahlen oder ein Set von Zahlen in dieser Form ohne Klassifikation verwendet. Diese sind nicht in den „Lernvorgang“ eingegangen. Das Ergebnis (Prediction) kann mit dem wahren Wert verglichen werden.
Die ML Methode
Als ML-Methode verwenden wir hier, anders als in der erwähnten Blog-Serie, ein Naive-Bayes Verfahren. Kurz erläutert, wertet das NB-Verfahren die Trainingsdaten aus und bestimmt – mittels der Bayes-Formel – die bedingte Wahrscheinlichkeit dafür, dass, gegeben eine m-stellige Zahl (Input-Vektor), das Ergebnis R=0 („gerade“) ist. Entsprechend für R=1 („ungerade“):
P(R=0|a0 a1 … am)
Der Input-Vektor ist einfach die Ziffernfolge der Zahl, wobei für die Dezimalstellen untereinander keine Abhängigkeit besteht. (Grundannahme für die Gültigkeit von „Naive“ Bayes.)
Im „gelernten“ Zustand kann das Modell (auch Classifier genannt) für unbekannte Zahlen b = b0 b1 … bm entscheiden, ob diese gerade oder ungerade ist, anhand der berechneten Wahrscheinlichkeiten P(R=0|b) und P(R=1|b) – je nachdem, welche der Wahrscheinlichkeiten größer ist.
(In der Regel reichen wenige Zahlen für das Training aus, sofern man die sog. Glättung im Classifier „ausschaltet“. Die Glättung kompensiert Fälle, in denen eventuell einzelne Werte in den Input-Daten nicht vorkommen (missing data), und sich damit Schwierigkeiten in der Auswertung ergeben können.)
Für unser gerade-ungerade-Lernen Problem zeigt sich, dass die o.a. Wahrscheinlichkeiten P entweder 0.0 oder 1.0 sind. Im Sinne der Blogserie haben wir es hier also mit „starkem Lernen“ zu tun.
Ist das Lernverfahren auch „robust“? In der Blogserie hatten wir damit ein Lernverfahren gekennzeichnet, das ein gewisses Maß an Fehlern in den Trainingsdaten vertragen kann und trotzdem „richtig“ lernt. Und dabei auch die Fehler „richtigstellt“ (im Code-Beispiel: 5% Zufallsstörung)
Da die Input-Werte ganzzahlig (Kategorien) sind (0,..9) und die Response-Klassen ebenfalls (0,1), setzen wir hier die Variante CategoricalNB() aus der scikit-learn Toolbox an.
Outline des Algorithmus „Gerade/Ungerade Lernen“
Als Programm liegt dieses Beispiel als ein Jupyter Notebook vor, ablauffähig und mit kleinen Zwischentexte zur Erläuterung. Wegen Problemen bei der Kompatibilität der Dokumentenformate liegt das Notebook als html-Datei hier: NB_even-odd_problem_notebook
Der übliche, grobe Ablauf ist wie folgt:
- Problem Defintion: Beschreibung der Aufgabe als Text
- Problem-Dimensionen und Datensatzumfang (Code-Zelle)
- Parameter für Problem-Varianten (optional, Code)
- Generierung des Datensets: (Code-Zellen) Inputzahlen per Zufallsgenerator, dargestellt als Liste von Dezimalziffern je Zeile, davon N Zeilen (Matrix-Struktur Nx6). Zugehörige Klassifikation (R-Werte) als Liste von 0 und 1 für jede Matrix-Zeile (Zahl). Beispiel:
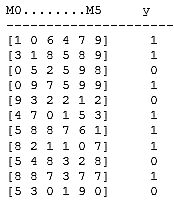
- Datenset-Aufteilung Tranings-/Testdaten: z.B. 70% zu 30% (Code)
- Categorical Naive Bayes Modell: Modell-Defintion und Training (g_u_model.fit()) mit den Trainingsdaten (Code)
- Ergebnisse: 7.1Test-Beispiele, 7.2 Genauigkeit der Klassifikation durch das Modell für Trainings- und Testdaten, 7.3 „Innere“ Daten des trainierten Modells (s. Code-Zellen)
- (Optional) Aufgaben-Varianten: 8.1 Verfälschen der Klassifikationen in den Trainingsdaten zur einem kleinen Prozentsatz per Zufall. 8.2 Probieren, Teilbarkeit durch 5 zu lernen. (Code Zellen)
- (Optional) Experimentieren: Teilbarkeit durch 3, 4 o.ä. Warum funktioniert Naiv-Bayes hier nicht?
Links zu NaiveBayes Methoden
https://scikit-learn.org/stable/modules/naive_bayes.html
https://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.CategoricalNB.html
https://www.analyticsvidhya.com/blog/2017/09/naive-bayes-explained/