„Hinter die Kulissen schauen“ – das heißt, die Effekte der Zwei- und Mehr-Qubit Algorithmen durch Zustandsübergänge zu erklären. Das ist, zugegeben, nicht ganz so einfach wie bei herkömmlichen Algorithmen, bei denen wir die Variablen – als Pendant zu den Qubits – einfach setzen, verrechnen und zu jeder Zeit „ansehen“ können (print).
In Q9 hatten wir die Darstellung von Qubit-Zuständen für 2-Qubit Systeme eingeführt – in Form von Vierer-Koordinaten und, alternativ, in Ket-Schreibweise. Damit können wir nun einige elementare Qubit-algorithmische Komponenten nachvollziehen. In Q9 hatten wir eine Reihe von Circuit-Beispielen grafisch erstellt und vom IBM Qubit-Simulator ausführen lassen. Einige davon wollen wir anhand der Zustandsübergänge untersuchen und so erklären, wie es zu den Messergebnissen kommt. Besonders interessiert uns natürlich das Phänomen der Verschränkung und, was es mit dem Kick-back auf sich hat.
Zwei-Qubit-Zustände können durch vier Koordinaten (w, x, y, z) dargestellt werden, die |w|²+|x²|+|y|²+|z|²=1 erfüllen. Also Punkte auf einer Art 4-dimensionalem Einheitskreis.
Wenn der Zustand aus einer Kombination von zwei Qubit-Zuständen, sagen wir (u,v) und (x,y), entsteht, dann sind die vier Koordinaten durch (u,v)⊗(x,y) = (ux, uy, vx, vy) bestimmt. Die Reihenfolge ist übrigens nicht vertauschbar! Und wir hatten per Circuit-Simulation und Nachrechnen schon gesehen, dass nicht jeder 2-Qubit-Zustand sich aus zwe 1-Qubit-Zuständen zusammensetzt (Verschränkung).
Zustände und Gates
Wir hatten schon in Q7 gesehen, dass man die 1-Qubit-Gates X und H durch die Koordinaten (x,y) eines Zustands ausdrücken kann:
X(x,y) = (y,x) und H(x,y) = 1/√2(x+y,x-y)
Ry hat einen Parameter, θ, der einen Drehwinkel beschreibt. Daher ist nicht Ry ein Gate sondern Ry(θ). Angewendet auf den Zustand (x,y), den man auch mittels seines Winkels auf dem Einheitskreis als (cos(α),sin(α)) ausdrücken kann, wirkt Ry(θ) auf (x,y) als „Bewegung“ auf dem Einheitskreis um θ/2. Als Formel also
Ry(θ)(x,y) = (cos(α+θ/2),sin(α+θ/2))
(Das θ/2 ist wieder nötig, weil der Ry-Paramter eine andere Bedeutung hat als der Drehwinkel auf unserem Einheitskreis.) Man kann das immer überprüfen durch Tests mit einfachen Composer-Circuits.
Aber was ist mit dem CNOT Gate, dass ja zwei Qubit-Zustände „verknüpft“? Nehmen wir wieder (u,v)⊗(x,y) = (ux, uy, vx, vy) als generelles Beispiel. Dann ist
CNOT angewendet auf (u,v)⊗(x,y) = (ux, vy, vx, uy)
d.h. die 2. und 4. Koordinate werden vertauscht. Aber wie können wir das begründen? Und welcher von beiden ist der „controlling“ (steuernde) Qubit-Zustand und welcher der „controlled“ (gesteuerte)? Wir überprüfen das mit dem Effekt auf die Basiszustände in Koordinatendarstellung. Wir erinnern uns dennoch, dass (1,0) dem Ket |0> entspricht und (0,1) dem Ket |1>.
(0,1)⊗(1,0) = (0, 0, 1, 0) —> CNOT —> (0, 0, 1, 0) = (0,1)⊗(1,0) gleich
(0,1)⊗(0,1) = (0, 0, 0, 1) —> CNOT —> (0, 1, 0, 0) = (1,0)⊗(0,1) ungleich
(1,0)⊗(1,0) = (1, 0, 0, 0) —> CNOT —> (1, 0, 0, 0) = (1,0)⊗(1,0) gleich
(1,0)⊗(0,1) = (0. 1, 0, 0) —> CNOT —> (0, 0, 0, 1) = (0,1)⊗(0,1) ungleich
Die Zustände der beiden Qubits bleiben nach CNOT gleich, wenn der zweite Zustand (rechts) (1,0) ist. Das entspricht dem Ket |0>. Der linke Zustand ändert sich, wenn der rechte (0,1) ist, was dem Ket |1> entspricht. Der rechts vom ⊗ stehende Zustand verändert sich in keinem Fall. Damit ist klar, dass der Zustand von q0 im Circuit 7 (Control Qubit) in der Formel rechts stehen muss, und der von q1 (Controlled Qubit) links im ⊗-Ausdruck. Merkregel: Das passt zu den Bit-Ketten, die beim Messen der Circuits geliefert werden: von q0 ganz rechts bis q4 ganz links.
Nur zur Übung hier die vierte Zeile „übersetzt“ in die Ket-Schreibweise.
|0>⊗|1> = |01> = 0*|00>+1*|01>+0*|10>+0*|11>
—> CNOT
—> 0*|00>+0*|01>+0*|10>+1*|11> =|11> = |1>⊗|1>
das q1 hat seinen Zustand von |0> auf |1> geändert, da q0 den Zustand |1> hat.
Wer Lust hat, kann die anderen CNOT-Transformationen ebenfalls in Ket-Schreibweise versuchen. (Die Kommentare unten werden gelesen!)
Verschränkte Qubits
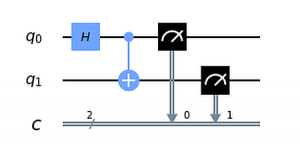 Hier noch einmal der Circuit 7, der uns eine Verschränkung der Qubits q0 (obere Leitung) und q1 (untere Leitung) bescherte. Bisher konnten wir nur die Messergebnisse interpretieren. Mit den Formeln für H und CNOT können wir den verschränkten 2-Qubit Zustand bestimmen.
Hier noch einmal der Circuit 7, der uns eine Verschränkung der Qubits q0 (obere Leitung) und q1 (untere Leitung) bescherte. Bisher konnten wir nur die Messergebnisse interpretieren. Mit den Formeln für H und CNOT können wir den verschränkten 2-Qubit Zustand bestimmen.
Die Ausgangszustände der beiden Qubits sind (1,0). Wenn H auf q0 angewendet wird, bekommen wir 1/√2(1,1) nach der Formel oben. Das CNOT müssen wir daher mit diesem Zustand als Control auf den Zustand von q1 anwenden, d.h. (1,0) steht links vom ⊗:
(1,0)⊗(1/√2,1/√2) = (1/√2, 1/√2, 0, 0) —> CNOT —> (1/√2, 0, 0, 1/√2) = ???
Das Ergebnis von CNOT ist 1/√2(1,0,0,1) und das ist, wie wir in Q9 gesehen haben, nicht separabel, d.h. in zwei einzelne Qubit-Zustände zerlegbar.
Im Beispiel 2 des vorigen Blogs (Q9) hatten wir die Variante mit einem X-Gate auf der q1-Linie, vor dem CNOT, diskutiert. In der vorausgegangenen Rechnung würde daher ganz links ein (0,1) stehen, statt (1,0). Was wäre dann hier der Zustand bei Messung? Und ist der separabel oder verschränkt?
Kick-back Qubit 0
Im Blog Q9 hatten wir mit Beispiel 6 einen überraschenden Effekt, der als Kick-back bezeichnet wird. Der Algorithmus im Composer-Format sah so aus:
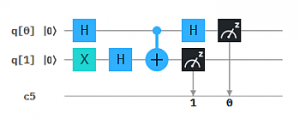 Die Messungen ergeben 01 und 11 zu je etwa 50%.
Die Messungen ergeben 01 und 11 zu je etwa 50%.
Wir versuchen das mittels der Abfolge der Zustände, die wir ja theoretisch berechnen können, zu verstehen. Wir verwenden dazu die Koordinaten-Darstellung der Zustände.
Qubit q0 beginnt im Zustand (1,0) und wird per H in (x,y) = 1/√2*(1,1) überführt. Qubit q1 beginnt im Zustand (1,0) und wird von X in (0,1) überführt. Darauf wird H angewendet, das nach der Formel oben den Zustand von q1 in (u,v) = 1/√2*(1,-1) überführt. Das 2-Qubit System hat damit den zusammengesetzten Zustand
(u,v)⊗(x,y) = (ux, uy, vx, vy) = 1/2*(1, 1, -1, -1)
—> CNOT (Vertauschen der zweiten und vierten Koordinate)
—> 1/2*(1, -1, -1 ,1) = 1/√2*(1,-1)⊗1/√2*(1,-1)
Nun überführt H, auf q0 im Zustand 1/√2*(1,-1) angewendet, q0 in (0,1). Qubit q1 bleibt in 1/√2*(1,-1). Wir stellen damit fest:
- Der 2-Qubit Zustand ist nicht verschränkt. Beide Qubits sind separat messbar.
- Messung von q0 liefert immer 1, Messung von q1 liefert 0 und 1 zu 50%. Damit erwarten wir die 2-Qubit Zustände 01 und 11 zu 50%.
Das controlled Qubit hat damit eine Rückwirkung (Kick-back) auf das q0. Es kehrt den Zustand von q0 zu (0,1) um, obwohl HH(1,0) = (1,0) zu erwarten wäre. Wir werden das Kick-back später in einem komplexeren Algorithmus geschickt einsetzen. (Zur Übung lohnt es sich, diese Rechnung auch in Ket-Form durchzuführen.)
Mehr Gates, mehr Qubits
Bisher haben wir folgende Gates und ihre Formeln für die Zustandsüberführung kennen gelernt: Das X, H und Ry für 1-Qubit Zustände, sowie ein „Reset“-Gate, das im Composer schlicht als |0> gekennzeichnet wird. Damit kann man im Verlauf der Zustandsentwicklung ein Qubit auf den Ausgangszustand zurücksetzten.
Das Instrumentarium der Qubit-Algorithmik enthält noch eine Reihe von weiteren Gates, die auch in einem Circuit eingesetzt werden können. Einige davon, die wir in unseren Blogs gebrauchen können, sind hier kurz erklärt. Wer Lust hat kann deren Wirkung unmittelbar in einfachen Circuits einmal ausprobieren – dabei ist aber zu beachten, dass verschiedene Zustände durchaus das gleiche Messergebnis liefern können.
- Y-Gate: Hat für unsere Zwecke die gleiche Wirkung wie X.
- Z-Gate: Überführt 1/√2*(1,1) in einem Schritt in 1/√2*(1,-1), und umgekehrt. Für diese beiden Zustände gibt es übrigens ein besonderes Ket-Symbol: |+> und |->. Es ist offensichtlich, welches Ket welchen Zustand kennzeichnet. Das Z-Gate überführt also |+> in |->. Klingt etwas exotisch, ist aber oft eine ganz praktische „Abkürzung“. Beide Zustände liefern natürlich das gleiche Messergebnis, daher kann man die Wirkung von Z nicht unmittelbar an der Messung ablesen.
- ID-Gate: Typisch Mathematik bzw. Informatik, es gibt immer auch eine Operation, die nichts verändert.
- Zwei-Qubit Gates:
- Swap-Gate, symbolisiert durch die zwei X, die übereinander stehen und mit einer senkrechten Linie verbunden sind: Vertauscht die Zustände der beiden betroffenen Qubits
- cH, controlled H-Gate: Analog zum CNOT führt es H für das controlled Qubit aus, wenn das controlling Qubit im Zustand |1> ist.
- Controlled Z-Gate, symbolisiert durch die zwei mit einem senkrechten Linie verbundene Punkte: Analog zum CNOT führt es Z für das controlled Qubit aus, wenn das controlling Qubit im Zustand |1> ist.
- Das Tofoli-Gate ist ein 3-Qubit Gate. Um das zu verstehen müssen wir zunächst unsere Zustandsbeschreibungen auf 3-Qubit Zustände erweitern.
Das machen wir gleich im Anschluß, ohne große Pause. Wir holen uns nur schnell einen Kaffe oder ein stilles Wasser. Dann gehts hier weiter.
Hier noch ein paar neue Begriffe aus diesem Anschnitt in Fortführung der tabellarischen Übersicht.
| Begriff englisch | Begriff deutsch | Bedeutung |
| CNOT-Gate | CNOT-Gatter | Controlled NOT – CNOT verknüpft zwei Qubits. In Abhängigkeit vom Zustand des einen Qubits ändert sich der des anderen. |
| Control | Control | Qubit, dessen Zustand beim CNOT Gate den des anderen „steuert“ |
| Controlled | Controlled | Qubit, dessen Zustand beim CNOT Gate durch den des anderen „gesteuert“ wird. |
| Y, Z, ID | Y, Z, ID | Weitere 1-Qubit Gates |
| 2-Qubit Gates | 2-Qubit Gates | Gates, die sich über zwei Qubits erstrecken |
| Swap-Gate | Swap-Gatter | 2-Qubit Gatter, vertauscht die Zustände zweier Qubits |
| cH-Gate | cH-Gatter | Controlled H-Gate, analog CNOT für H |
| cZ-Gate | cZ-Gatter | Controlled Z-Gate, analog CNOT für Z |
| Tofoli-Gate | Tofoli-Gatter | Ein controlled 3-Qubit Gate. Eine Art Erweiterung des CNOT auf 2 steuernde Qubits. |
| |+>, |-> | |+>, |-> | Ket-Bezeichnung für 1/√2(1,1) bzw. 1/√2(1,-1) |
