So sieht ein Circuit mit 3 Qubits im IBM Q Composer aus.
3-Qubit Zustände
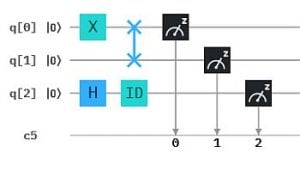 Wir haben hier auch gleich einmal das Swap-Gate zwischen q0 und q1 eingesetzt und das ID-Gate.
Wir haben hier auch gleich einmal das Swap-Gate zwischen q0 und q1 eingesetzt und das ID-Gate.
Was wird das Messergebnis sein? Klar, q0 liefert 0, q1 liefert 1, beides jeweils zu 100%. Aber H (mit oder ohne ID) liefert für q2 je 50% 0 und 1. D.h. als 3-Qubit Messergebnis können wir 010 und 110 zu je 50% erwarten. (Der Lauf auf dem Simulator bestätigt die Erwartung.)
Erstaunlich – dies ist die Analyse eines Mini-Qubit-Algorithmus mit immerhin 3 Qubits, die wir allein aus der Interpretation der Gates abgeleitet haben. Das war übrigens auch schon bei den vergangenen Circuit-Beispielen der Fall. Andererseits kann man den Algorithmus auch „formelmäßig berechnen“, indem man, ausgehend vom Anfangszustand der Qubtis, die Abfolge der Zustände über die Gate-Formeln berechnet. Das haben wir ernsthaft schon in Q10 begonnen.
Nun zu den 3-Qubit-Zuständen. Mit dem allgemeinden Zustand (r,s) für q2 rechnen wir analog zum 2-Qubit-Zustand:
(r,s) ⊗ ((u,v)⊗(x,y)) = (r,s) ⊗ (ux, uy, vx, vy) = (rux, ruy, rvx, rvy, sux, suy, svx, svy)
Das Resultat ist ein 8-dimensionalen „Punkt“. Wieder ist die Summe der Quadrate der Koordinaten =1. Und alle 8-Koordinaten-Punkte, die diese Bedingung erfüllen sind wieder zulässige 3-Qubit-Zustände. Die Berechnung des 3-Qubit-Zustands aus den Zuständen der einzelnen Qubits ist assoziativ aber nicht kommutativ. D.h. es ist zwar egal, ob erst (r,s)⊗(u,v) gerechnet wird oder erst (u,v)⊗(x,y), aber es ist nicht egal, ob man die Reihenfolge der Qubit-Zustände vertauscht: (r,s)⊗(u,v) ist nicht das Gleiche wie (u,v)⊗(r,s). Nur zur Warnung!
Verfolgen wir die Zustände im obigen Beispiel:
q0 (1,0) —> X —> (0,1) —> Swap —-> (1,0) = (x,y)
q1 (1,0) ———————> Swap —-> (0,1) = (u,v)
q3 (1,0) —> H —> 1/√2(1,1) —> ID —>1/√2(1,1) = (r,s)
Damit wird der 3-Qubit-Zustand zum Zeitpunkt der Messung
1/√2(1,1) ⊗ (0,1) ⊗ (1,0) = (0, 0, 1/√2, 0, 0, 0, 1/√2, 0)
Man macht sich hier zunutze, dass der 3-Qubit-Zustand separabel ist; denn er wird ja aus drei 1-Qubit-Zuständen zusammen gesetzt.
Messung und Kets
Wie passt das zur Messung? Dazu müssen wir den M-Operator auf 3-Qubit-Zustände erweitern. Ein solcher Zustand (a0, a1, a2, a3, a4, a5, a6, a7) lässt sich mit 3-Kets schreiben als a0|000>+a1|001>+a2|010>+a3|011>+a4|100>+a5|101>+a6|110>+a7|111>
Dabei sind die 3-Kets wieder die Abkürzungen für |0>⊗|0>⊗|0> = |000> usw. Allgemein gilt die Schreibweise |ijk> = |i>⊗|j>⊗|k>.
Und da wir gerade dabei sind, stellen wir fest, dass die 0-1-Folgen in den 3-Kets genau die Dezimalzahlen 0, 1, 2, …, 7 ergeben, wenn man sie als Binärzahlen interpretiert. Und wenn wir die Koordinaten a0, … a7 so durchnummerieren wie in der Ket-Summe, dann passen die gerade zu den Kets als Dezimalzahlen.
Damit kann man nun den Operator M so festlegen – und das gilt für beliebige Anzahlen von Qubits:
M(a0, a1, a2, a3, a4, a5, a6, a7) = (|a0|², |a1|², |a2|², |a3|², |a4|², |a5²|, |a6|², |a7|²)
und dabei bedeutet z.B. |a5|² die Wahrscheinlichkeit dafür, dass wir als Messergebnis 101, die Binärzahl für 5, bekommen. Und ja, man schreibt dann natürlich auch manchmal den Ket mit der Dezimalzahl statt der Bitkette: |101> = |5>. Allgemein:
|i>⊗|j>⊗|k>=|ijk>=|d>, wobei d=i*2²+j*2¹+k*2°
Dabei den Durchblick zu behalten, ist schon eine ziemliche Herausforderung. Aber es musste mal gesagt werden – auch wenn wir möglichst bei der Koordinatendarstellung von Zuständen bleiben.
Zurück zur Messung im Beispiel oben: der M-Operator angewendet auf den 3-Qubit-Zustand
1/√2(1,1) ⊗ (0,1) ⊗ (1,0) = (0, 0, 1/√2, 0, 0, 0, 1/√2, 0)
ergibt die Wahrscheinlichkeiten (0,0,1/2,0,0,0,1/2,0). D.h. nur 010 und 110 kommen bei Messungen vor.
Man muss darauf achten, dass man Zustände in Koordinatenschreibweise und Messwahrscheinlichkeiten sachlich und sprachlich voneinender unterscheidet. Insofern ist die Ket-Schreibweise wiederum hilfreich, weil sid ganz anders „aussieht“ als die Liste der Wahrscheinlichkeiten, die M liefert.
Tofoli Gate
Das Tofoli-Gate ist ein CCNOT Gate, d.h. q0 und q1 steuern q2: wenn beide im Zustand (0,1) sind (also |1> als Ket), wird der Zustand von q2 umgedreht, sonst bleibt er unverändert. Mit (x,y), (u,v) und (r,s) als Zustände von q0, q1 bzw. q2, überführt das Tofoli-Gate den 3-Qubit-Zustand
(r,s) ⊗ (u,v)⊗(x,y) = (rux, ruy, rvx, rvy, sux, suy, svx, svy)
—> CCNOT
—> (rux, ruy, rvx, svy, sux, suy, svx, rvy)
d.h. die 4. und 8. Koordinate werden vertauscht. Das ist einfach zu verstehen: v und y sind die Anteile von (0,1) (oder |1>) in den beiden Control-Qubits q0 und q1. Kommen beide zusammen in einer Koordinate des 3-Qubit-Zustands vor, wechselt q2 die Zustandskoordinaten. Damit wird in der 4. Koordinate rvy zu svy und umgekehrt in der 8. Koordinate.
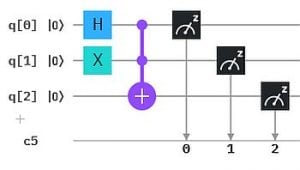 Ein Beispiel-Circuit mit Tofoli-Gate (CCNOT). Es liefert 010 und 111 mit Wahrscheinlichkeit 1/2. Eine gute Übung, das Ergebnis über die Zustandsentwicklung nachzuvollziehen.
Ein Beispiel-Circuit mit Tofoli-Gate (CCNOT). Es liefert 010 und 111 mit Wahrscheinlichkeit 1/2. Eine gute Übung, das Ergebnis über die Zustandsentwicklung nachzuvollziehen.
Logische Gates
Wenn wir das Tofoli-Gate (auch CCNOT oder ccX genannt) mit den Controlled Gates in den 2-Qubit-Circuits vergleichen, etwa cX (CNOT) oder cH, dann ist das Tofoli-Gate eine Erweiterung des CNOT auf zwei „kontollierende“ Qubits. Entsprechend kann man auch andere 1-Qubit Gates-Gates über kontrollierende Qubits beeinflussen.
Bei 3-Qubit gibt es auch die Möglichkeit, ein controlling Qubit auf die zwei anderen Qubits wirken zu lassen. Ein Beispiel ist das cSWAP, auch Fredkin-Gate genannt. Es „swappt“ die Zustände von q1 und q2 in Abhängikeit von q0.
Nicht alle Möglichkeiten für controlled Gates sind als Symbole im Circuit Composer vordefiniert. Man kann sie aber in der Regel alle aus vorhandenen Gates „konstruieren“.
Die logischen Qubit Gates sind zu vergleichen mit einfachen „wenn … dann“ Konstrukten in herkömmlichen Algorithmen. Während dabei aber die Bedingung hinter „wenn“ stets entweder wahr oder falsch ergibt, oder als Bits 1 oder 0, kann bei Qubits die Bedingung „anteilweise“ erfüllt sein. Etwa, wenn das Control-Qubit den Zustand 1/√2(1,1) hat. Die Wirkung nach dem „dann“ bezieht sich immer auf ein anderes Qubit (das controlled Qubit), während bei herkömmlichen Algorithmen die „dann“-Aktion mehrere Schritte mit mehreren Variablen haben kann – die in der „wenn“-Bedingung vorkommenden eingeschlossen.
3-Qubit-Verschränkungen
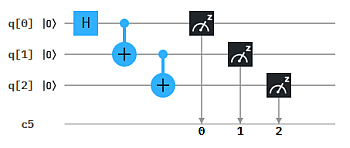 Natürlich gibt Verschränkung auch in 3-Qubit (oder Mehr-Qubit) Systemen. Der Circuit sieht aus wie ien Erweiterung unseres Circuit 7 für 2 Qubits. Tatsächlich ist auch das Messergebnis ähnlich: Es liefert 000 und 111 mit jeweils etwa 50%. Das lässt sich auch anhand der Zustandsabfolge nachvollziehen (mit ein bisschen Probieren):
Natürlich gibt Verschränkung auch in 3-Qubit (oder Mehr-Qubit) Systemen. Der Circuit sieht aus wie ien Erweiterung unseres Circuit 7 für 2 Qubits. Tatsächlich ist auch das Messergebnis ähnlich: Es liefert 000 und 111 mit jeweils etwa 50%. Das lässt sich auch anhand der Zustandsabfolge nachvollziehen (mit ein bisschen Probieren):
(1,0)⊗(1,0)⊗(1/√2,1/√2) = (1/√2, 1/√2, 0, 0, 0, 0, 0, 0)
—> CNOT-q0-q1 —> (1/√2, 0, 0, 1/√2, 0, 0, 0, 0)
—> CNOT-q1-q2 —> (1/√2, 0, 0, 0, 0, 0, 0, 1/√2)
Verschränkte 2- und Mehr-Qubit-Zustände spielen eine wichtige Rolle in Qubit-Algorithmen. Wir werden das in den nächsten Blogs demonstrieren.
Man kann nun untersuchen, was passiert, wenn man dem q1 und / oder dem q2 ein X-Gate voranstellt, d.h. nicht mit dem Anfangszustand (1,0) sondern mit (0,1) startet. Das Einfachste, wenn man den Zugang zum IBM Q Experience Circuit Composer hat, ist Ausprobieren. Andererseits kann man das auch erschließen. Z.B. hat ein X auf der q1-Linie den Effekt, als Messergebnis 001 und 110 zu liefern, also gegenüber 000 und 111 eine Umkehrung des (rechten) Ergebnis-Bit aus dem Zustand von q0. In jedem Fall bekommen wir eine Verschränkung der 3 Qubits.
Diese Zustandsverschränkung wird als GHZ-Verschränkung bezeichnet – wie überhaupt in der Qubit-Welt viele Objekte mit Namen von Forschern bezeichnet oder abgekürzt werden. Damit wollen wir uns hier aber nicht belasten. Ganz am Ende der Blogserie gibt es dann noch mal eine Tabelle dafür. Ein weiterer wichtiger Verschränkungszustand heißt „W-Zustand“. Den werden wir im nächsten Blog kennen lernen. Und unterwegs werden wir einen ersten „richtigen“ Qubit-Algorithmus konstruieren, der etwas Reales tut: „Würfeln“. Klingt simpel? Ist es aber nicht.
Kleine Pause, dann geht’s hier weiter. Stay tuned!
Tabellen-Ergänzung
| Begriff englisch | Begriff deutsch | Bedeutung |
| Swap Gate | Swap Gate | Vertauscht die Zustände zweier Qubits |
| 3-Qubit State | 3-Qubit-Zustand | (r,s)⊗(u,v)⊗(x,y) in Koordinatenschreibweise |
| |ijk> | |ijk> | 3-Qubit-Zustand in Ket-Schreibweise: |ijk> = |i>⊗|j>⊗|k> |
| associative | assoziativ | Reihenfolge der Ausführung der Operation ist beliebig z.B. (a+b)+c = a+(b+c). |
| commutative | kommutativ | Reihenfolge der Operanden ist beliebig, z.B. a+b=b+a. Aber nicht a-b = b-a! |
| Tofoli-Gate | Tofoli-Gatter | ccX: Switch q3, wenn q0 und q2 im Zustand (0,1) |
| Fredkin-Gate | Fredkin-Gatter | cSwap: Swappt Zustände von q2 und q3, wenn q0 in (0,1) |
| GHZ | GHZ | Ein verschränkter 3-Qubit-Zustand |
| W state | W-Zustand | Ein anderer 3-Qubit verschränkter Zustand |
