Ein normaler Spiel-Würfel hat sechs Flächen mit Punkten (Augen) von 1 bis 6. Bei Games oder Simulation von Zufallsvorgängen werden Würfel, oder allgemein Zufallszahlen, durch trickige mathematische Verfahren imitiert. Pseudo-Zufallszahlen heißen sie deshalb, weil sie nicht echt zufällig sind, sondern das Ergebnis einer festgelegten Berechnungsformel. Die ist für uns nur so kompliziert, dass wir das Ergebnis nicht wirklich „verstehen“ oder vorhersagen können. Also akzeptieren wir das als „Zufall“, obwohl es genau berechnet ist.
Der Spiel-Würfel ist echt. Da gibt es keine Funktion, nach der wir das Ergebnis eines Wurfs berechnen könnten. Wirklich nicht? Nun ja, prinzipiell doch, denn er gehorcht ja klaren physikalischen Gesetzen in dem, wie er sich dreht, wie er fällt, wie er rollt, wie er kippt. Aber auch diese alle zusammen sind wieder so kompliziert, dass wir gut darauf vertrauen können, dass er ein „neutrales“ Zufallsergebnis liefert.
Der Quanten-Würfel ist nicht nur echt, sondern es ist sogar prinzipiell nicht möglich das Ergebnis voraus zu berechnen. Prinzipiell heißt hier, nach den Prinzipien der Quantenphysik. Zugegeben, es ist schwer, das zu glauben – aber man kann das sogar beweisen, d.h. die Physiker können das.
Wenn wir also einen Qubit-Algorithmus entwerfen können, der Würfelergebnisse durch Messung liefert, und wenn wir den auf einem echten Quantencomputer laufen lassen würden, hätten wir einen wirklich echten Würfel.
Ein Würfel-Qubit-Algorithmus
Einen einfachen Zufallsgenerator, der wie beim Münzwurf 0 oder 1 liefert, kennen wir schon: Wir versetzen ein Qubit in den Zustand |+> = H|0> und messen. Das ergibt ein Bit. Wir können das dreimal tun und erhalten ein 3-Bit-Ergebnis, von 000 bis 111. Das sind allerdings 8 mögliche Ergebnisse, für den Würfel brauchen wir genau 6 mit gleicher Wahrscheinlichkeit 1/6.
In der Zahl sechs liegt hier unser kleines Problem. Mit 2 Qubits können wir bis zu 4 verschiedene 2-Qubit-Messergebnisse erzielen. Wir kennen bereits Circuits, die ein, zwei, oder vier 2-Bit Ergebnisse liefern. Wir werden sehen, dass man auch Circuits konstruieren kann, die drei davon liefern mit gleicher Wahrscheinlichkeit. Aber auch das ist schon nicht so einfach.
Wir benötigen sechs, also brauchen wir 3 Qubits. Es ist einfach damit 1, 2, 4 oder 8 3-Bit Messergebnisse mit Häufigkeit größer Null zu erzielen. Aber sechs?
Wir versuchen folgende Methode:
Wir zerlegen das Problem in zwei Teilprobleme 6 = 3*2 : (a) die Konstruktion eines Circuits, der drei gleichwahrscheinliche Messergebnisse liefert, (b) eine Erweiterung, die den Endzustand von (a) noch in zwei gleichwahrscheinliche aufteilt.
Während (b), gefühlt, einfach erscheint – wir kennen ja die Wirkung von H – ist (a) etwas komplizierter. Aber auch hier teilen wir wieder auf: Wir brauchen einen Cicruit, der zwei Ergebnisse im Verhältnis 1/3 : 2/3 liefert, und versuchen dann, die 2/3 wieder in zwei gleichwahrscheinliche Ergebnisse „aufzuteilen“.
Klingt, als könnte das gehen – aber wie? Zwei Ergebnisse mit unterscheidlichen Häufigkeiten hatten wir schon in Q8 für 1 Qubit erzeugt, durch Drehung mit Ry. (Das Schöne an den Qubit-Algorithmen ist, dass wir unsere Ideen – auch schrittweise – immer gleich überprüfen können mit dem IBM Composer und qasm-Simulator!) Also probieren wir mal:
Der Zustand auf dem Einheitskreis mit den Koordinaten (1/√3, 2/√3) liefert das gewünschte Ergebnis: (1,0) mit 1/3 und (0,1) mit 2/3 Wahrscheinlichkeit. Wie kommen wir vom Ausgangszustand (1,0) dahin? Es gibt verschiedene Wege. Der einfachste ist mittels einer Drehung um den passenden Winkel. Hier muss man den Taschenrechner bemühen und z.B. die arccos-Funktion mit 1/√3 aufrufen. Der Drehwinkel ist damit 0.955317. Wenn wir diesen mit Ry realisieren wollen, müssen wir wieder daran denken, dass der Ry-Winkel immer als das Doppelte vom Winkel im Koordinatensystem genommen werden muß (s. Q8). Wir komponieren also
|0> —> Ry(2*0.955317) —> M (Messung) —> 000 und 001 zu 1/3 bzw 2/3
Der Simulationslauf bestätigt das!
Nun müssten wir 001 noch „aufteilen“ in zwei Ergebnisse mit je 1/2 Wahrscheinlichkeit. Das wird trickig. Die 2/3 kommen aus der Komponente |1> des q0-Zustands. Die können wir mit einem geeigneten controlled Gate auf ein zweites Qubit „übertragen“ werden. Sie müssen aber auf die Zustände |0> und |1> von q1 1:1 aufgeteilt werden. Damit würde der |1>-Anteil von q0 kombiniert werden mit den beiden Basiszuständen von q1. Gleichzeitig darf aber der |0>-Anteil von q0 nicht mit einem |1>-Anteil von q1 kombiniert werden, denn sonst hätten wir wieder 4 Ergebnisse. Was bietet sich an? Das controlled Hadamard-Gate! Das lässt zum Teil den q1 Ausgangszustand |0> unberührt und zum anderen Teil „dreht“ es diesen auf 1/√2(|0>+|1>). Hier ist das Composer-Diagramm dazu.
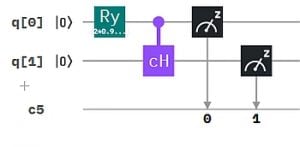 Die Läufe auf dem Simulator liefern das gewünschte Ergebnis: 00, 01 und 11 mit Häufigkeiten z.B. 31.25%, 34.18% und 34.57%. Wie oben erwähnt haben wir hiermit auch ein Beispiel für ein 2-Qubit-System, das 3 der vier möglichen Messergebnisse aufweist.
Die Läufe auf dem Simulator liefern das gewünschte Ergebnis: 00, 01 und 11 mit Häufigkeiten z.B. 31.25%, 34.18% und 34.57%. Wie oben erwähnt haben wir hiermit auch ein Beispiel für ein 2-Qubit-System, das 3 der vier möglichen Messergebnisse aufweist.
Wir wollten aber einen Würfel konstruieren. Für Schritt (b) brauchen wir nur ein weiteres Qubit in eine 1:1 Superposition zu bringen. Dann bekommen die 3 2-Qubit Ergebnisse von (a) jeweils eine 0 oder 1 „dazugeschaltet“. Das geht am einfachsten mit dem Hadamard-Gate. Das Composer-Diagramm und ein Ergebnis-Histogramm von 1024 Shots:
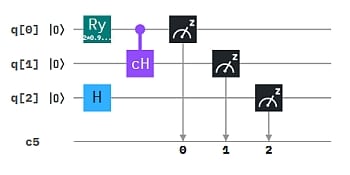
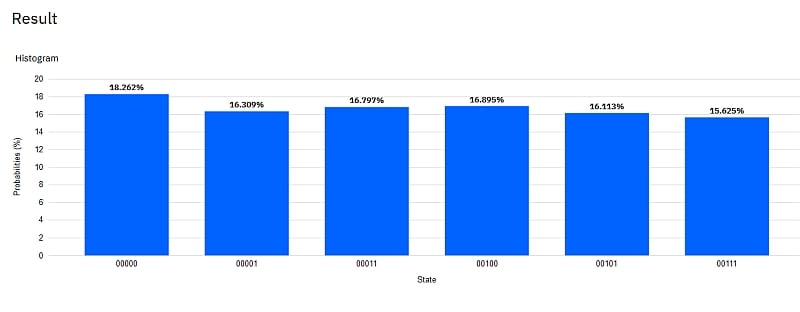 Das Ergebnis-Histogramm zeigt die 6 „Würfel-Ergebnisse“ mit etwa gleicher Häufigkeit. Natürlich sind die Bit-Ketten unter den Säulen nicht als Binärzahlen zu nehmen. Eine Interpretation als Augenzahl ist allerdings simpel. (Wir werden an anderer Stelle ein Würfelspiel in Form eines Python Programms unter Verwendung des IBM QC-Package Qiskit zeigen.) Wir können z.B. folgende Übersetzung festlegen
Das Ergebnis-Histogramm zeigt die 6 „Würfel-Ergebnisse“ mit etwa gleicher Häufigkeit. Natürlich sind die Bit-Ketten unter den Säulen nicht als Binärzahlen zu nehmen. Eine Interpretation als Augenzahl ist allerdings simpel. (Wir werden an anderer Stelle ein Würfelspiel in Form eines Python Programms unter Verwendung des IBM QC-Package Qiskit zeigen.) Wir können z.B. folgende Übersetzung festlegen
| Qubit-Ergebnis | 00000 | 00001 | 00011 | 00100 | 00101 | 00111 |
| Augenzahl | 2 | 1 | 3 | 4 | 5 | 6 |
Dann sind immerhin die mittleren vier Augenzahlen in den Bitketten als Binärzahl repräsentiert.
Die W-State Verschränkung
Die Idee für den obigen, letztlich doch recht einfachen Qubit-Algorithmus für einen Würfel, geht auf einen Artikel zurück, in dem P. Decoodt in einem GitHub Beitrag von 2019 (Link) die Erzeugung sog. verschränkter W-Zustände beschreibt.
W-Zustände können beliebig viele Qubits in der Weise verschränken, dass jedes darin nur einmal mit ihrem Basiszustand |1> vertreten sind. Also etwa
1/√2(|01>+|10>) für n=2 Qubits
1/√3(|001>+|010>+|100> für n=3, und
1/√n(|00…01>+|00…10>+….+|10…00>) allgemein.
Für n=3 sieht man, dass der W-Zustand bei Messung genau 3 Ergebnisse mit gleicher Wahrscheinlichkeit liefert. Daher ist er ein guter Kandidat für den Schritt (a) eines Würfel-Algorithmus. Es gibt in dem erwähnten Beitrag einen sehr eleganten Algorithmus, bzw. ein algorithmisches Schema, nach dem die W-Zustände für n Qubits generiert werden können. Für n=3 und in Composer-Darstellung übersetzt, sieht das wie folgt aus:
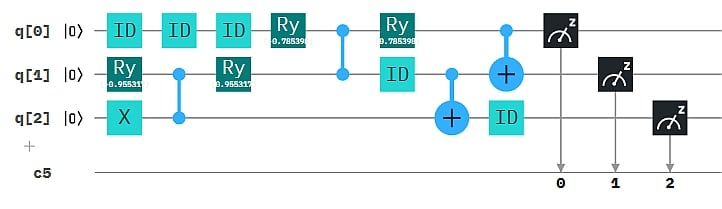
(Die ID Gates kann man sich weg denken. Sie stehen dort nur, damit die elegante Struktur des Algorithmus deutlich wird. Der Composer schiebt ansonsten alles zusammen, was die Ausführungsabfolge nicht beeinträchtigt.) Was man hier an der Grafik nicht erkennt, ist, dass die cZ-Gates in diesem Algorithus „von unten nach oben“ weisen. D.h. die Control-Qubits sind q2 und q1, die Target-Qubits q1 bzw q0. Die „Richtung“ lässt sich im cZ-Gate editieren.
Der Algorithmus liefert drei mögliche Messergebnisse: 001, 010 und 100. Und die zusätzliche Idee für einen echten Würfel besteht damit nur noch darin, diese drei zu gleichen Anteilen „aufzuspalten“. Da kommt das Hadamard-Gate gerade recht, das am Ende der q2-Lebenslinie hinzugefügt wird. In der Abbildung also nach dem ID-Gate und vor den Messoperatoren.
Insgesamt ist der W-Zustand Algorithmus als Teil des Würfel-Algorithmus aber recht komplex, daher lohnt es, sich die einzelnen Schritte des genauer anzusehen. Zunächst stellt man fest, dass die beiden CNOT Gates nicht nötig sind, um auf genau drei verschiedene Messergebnisse zu kommen. Auch hier ist es gute Praxis, die Messpunkte im Composer einfach zu verschieben, um zu überprüfen, was der bis zu einer bestimmten Stelle im Algorithmus entwickelte Zustand ergibt. Setzt man die Messpunkte z.B. hinter das zweite Ry-Gate auf der q0-Linie, bekommt man zwei Messergebnisse im Häufigkeitsverhältnis 1/3 : 2/3. (Allerdings nicht den W-Zustand. Der ist aber auch für den Würfel unerheblich.)
Die nächste Vereinfachnung ergibt sich, wenn man bedenkt, dass das X anfangs der q2-Linie nur den q2-Zustand so umstellt, dass das controlled Z (cZ, senkrechte Linie mit zwei Punkten) immer greift. Man kann also das X und das cZ weglassen, wenn man dafür ein Z an diese Stelle auf der q1-Linie platziert. Das bedeutet aber, dass sich der Zustand von q1 zunächst unabhängig entwickelt: Eine Drehung in negative Richtung um einen bestimmten Winkel θ, eine Spiegelung an der x-Achse (Wirkung des Z-Gates), was insgesamt einer Drehung des Ausgangszustands um θ in positiver Richtung (in den 1. Quadranten des Koordinatensystems) entspricht. Anschließend erfolgt eine Drehung noch einmal um θ, so dass wir insgesamt bei einem Winkel von 2*θ ankommen. Daher kann man das ganze Geschehen auch abkürzen, indem man statt dessen für q1 nur eine Drehung (Ry) um 2*θ in positiver Richtung als Gate ansetzt. Nun muss man θ so festlegen, dass der Zustand die zwei Messergebnisse im Verhältnis 1/3 : 2/3 liefert. Dieser Winkel ist im W-Algorithmus bereits bestimmt (0.955317 oder arccos(1/√3) ), man kann ihn also übernehmen. Mit dem Composer kann man das Ergebnis unmittelbar überprüfen.
Es bleibt die Überlegung für das Zusammenspiel zwischen q1 und q0. Der Zustand von q0 wird zunächst ebenfalls (per Drehung) verändert. Dann greift das cZ: die Wirkung des Z-Gates beschränkt sich auf den |1> Anteil des q1-Zustands. Mit diesem Anteil wird der q0-Zustand gespiegelt und anschließend noch einmal um φ in positiver Richtung gedreht. Dieser „Anteil“ ist damit in einem Zustand, der im Koordinatensystem mit dem Winkel 2*φ auf dem Einheitskreis liegt. Der andere Anteil des q0-Zustands wird lediglich wieder „zurück gedreht“ auf den Ausgangszustand |0>. Der Winkel φ muss so bestimmt werden, dass der zugehörige Zustand zur Hälfte aus |0> und zur Hälfte aus |1> besteht. Das kann man aber insgesamt auch erreichen, indem man die Drehungen mit dem Ry-Gate und das cZ ersetzt durch ein einfaches controlled H (cH) „von q1 nach q0“. Genau das haben wir oben getan, was uns zu dem schlichten Würfel-Algorithmus oben geführt hat. (Allerdings haben wir dort q0 und q1 vertauscht.)
Wir lernen daraus auch eine Methode des Qubit-algorithmischen Denkens: Effekte von Gates zu verstehen und parallel mit Hilfe des einfachen grafischen Composer Tools zu überprüfen, indem man systematisch Messpunkte setzt bzw. verschiebt. Verschieben eignet sich insbesondere für die Analyse von Qubit-Algorithmen, das systematische Setzen beim Entwurf von Qubit-Algorithmen.
Die Erläuterung der Wirkung von cZ oder auch des cH zwischen q1 und q0 macht auch deutlich, warum man zu der Deutung neigt, dass ein Qubit „in zwei Zuständen gleichzeitig“ sein kann – vereinfacht zu: „Ein Qubit kann gleichzeitig 0 und 1 sein“. Mittels controlled Gates kann ein Zustand, der eine Superposition (i.e. Linearkombination) darstellt, eingesetzt werden, um ein anderes Qubit auf zwei unterschiedlichen „Wegen“ weiter zu entwickeln. Es ist, als würde man gleichzeitig zwei „Schicksale“ des gleichen Qubit verfolgen. Von da aus ist es nicht weit bis zu der phantastischen Vorstellung von gleichzeitig existierenden Parallelwelten. Wir kommen darauf in einem späteren Blog noch einmal zurück.
Der rekursive W-State Algorithmus hat interessantes Potenzial über die Würfel-Implementierung hinaus. Wir können damit im Prinzip jede Anzahl von Messergebnissen realisieren. Z.B. mit n=5 Verteilungen über 5 Bitketten der Länge 5. Und mit „Aufspaltungen“ wie oben in Schritt (b) bei n=3 auch gerade Vielfache davon.
Im nächsten Abschnitt versuchen wir uns am Super Dense Coding, bei dem man mit n Qubits 2n Bits an Information übertragen kann. Ebenfalls eine Quelle vieler Mythen.
Vorher aber eine Spiel-Pause – mit dem Quantenwürfel. Stay tuned!
Tabllen-Ergänzung
| Begriff englisch | Begriff deutsch | Bedeutung |
| Pseudo random numbers | Pseudo-Zufallszahlen | Mit einer determinierten Rechenvorschrift erzeugte Zahlen, die uns „zufällig“ erscheinen |
| Histogram | Histogramm | Säulen-Darstellung von Zahlenwerten, z.B. Häufigkeiten von Ereignissen |
| W State | W-Zustand | Verschränkter n-Qubit Zustand besonderer Struktur |
| Target Qubit | Ziel-Qubit | Andere Bezeichnung für das Controlled Qubit bei einem Controlled Gate |
| Algorithmic schema | Algorithmisches Schema | Allgemeine Struktur von Algorithmen, die mehreren Algorithmen zugrunde liegen kann. |
| ID Gates | ID-Gatter | Wirkungsloses Gatter, das i.w. zu besseren Strukturierung von Composer Grafiken verwendet werden kann. Auch für zeitliche Taktung. |
| Qubit Algorithmic Thinking | Qubit-algorithmisches Denken | Verstehen, Analysieren und Entwerfen von Qubit-Algorithmen als speziellem Algorithmus-Typ |
1 Kommentar
Kommentarfunktion ist geschlossen.

[…] Pause, dann geht’s hier weiter. Stay […]