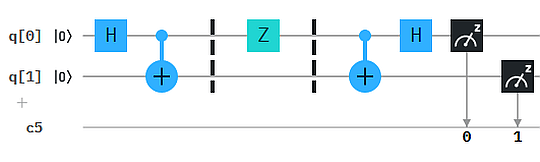
Auf verschränkten Qubits lassen sich eine Reihe interessanter Effekte aufbauen – mit noch interessanteren Namen: Superdense Coding, Quanten-Kommunikation und Quanten-Teleportation sind sicher die spektakulärsten.
Superdense Coding bedeutet, dass man 2 Bit Information in einem Qubit „speichern“ kann. Quanten-Kommunikation ermöglicht sichere Übertragung von 2 Bits durch ein Qubit und Quanten-Teleportation umgekehrt die Übertragung eines Qubit-Zustands durch 2 Bits. Wie das Qubit-algorithmisch geht und was das bedeutet, untersuchen wir in diesem Abschnitt. Falls der zu lang wird, lagern wir die Quanten-Teleportation auf den nächsten Blog aus.
Superdense Coding – Naiver Versuch und Bit-controlled Qubits
Wir werden die Idee des Superdense Coding zunächst auf einem Weg angehen, der naheliegend scheint, sich aber als Irrweg herausstellen wird. Wir können dabei jedoch eine interessante Möglichkeit der Qubit-Algorithmik kennen lernen: Das Zusammenspiel von klassischen Bits und Qubits: Bit-controlled Gates, manchmal auch Dependent Gates genannt.
Wir haben bereits kennen gelernt, wie man über den Zustand eines Qubit den eines anderen „steuern“ kann: Controlled Gates. Es gibt bei Qubit-Algorithmen auch die Möglichkeit, Qubit Zustände durch klassiche Bits zu beeinflussen. Dabei wird, analog zum Controlled Gate, ein Qubit-Gate durch eine Bedingung gesteuert, in die die Bits eines Messergebnisses einbezogen werden. Wir nennen das hier Bit-controlled Gates.
Mit dem Composer wird ein Bit-controlled Gate dadurch erzeugt, dass das Gate auf einer Qubit-Linie mit dem If-Operator kombiniert wird. Das If-Symbol wird dazu einfach auf das Gate gezogen (Drag&Drop). Anschließend kann man das Gate editieren, d.h. die If-Bedingung nach Bedarf festlegen. Die If-Bedinung kann nur als Vergleich der gemessenen Bit-Kette (auf der c-Linie) mit einem Zahlenwert formuliert werden. Dabei werden die Bits der Messung als Binärzahl gewertet. (Mit der Qiskit-Bibliothek für Python sind das natürlich einfache If-Konstrukte, die sich auf die Mess-Bits beziehen.)
Hier ein Beispiel.
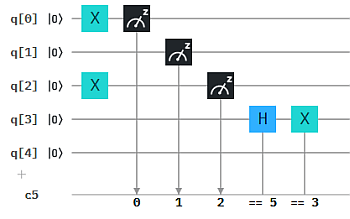 Die Qubits q0, q1, q2 werden in die Zustände |1>, |0> bzw |1> versetzt und gemessen (1 shot) . Das ergibt die 3-Bit-Kette 00101, die Binärzahl für 5. Für Qubit q3 wird das Hadamard-Gate H angewendet, wenn das Messergebnis 5 ist. Wenn es 3 ist, wird dagegen X angewendet – also nicht im vorliegenden Fall. Bei allen anderen Messergebnissen passiert nichts mit q3.
Die Qubits q0, q1, q2 werden in die Zustände |1>, |0> bzw |1> versetzt und gemessen (1 shot) . Das ergibt die 3-Bit-Kette 00101, die Binärzahl für 5. Für Qubit q3 wird das Hadamard-Gate H angewendet, wenn das Messergebnis 5 ist. Wenn es 3 ist, wird dagegen X angewendet – also nicht im vorliegenden Fall. Bei allen anderen Messergebnissen passiert nichts mit q3.
Das Beispiel zeigt auch gleich einen einfachen Weg wie man Bits „von außen“ in einen Circuit hineinbringen kann.
Die naheliegende Idee, zwei Bits in einem Qubit zu speichern, wäre, für die vier möglichen Kombinationen 00, 01, 10, 11 vier Superpositionen eines Qubit zu definieren, die durch Bit-gesteuerte Gatter erzeugt werden. Wir können zum Beispiel die Zwei-Bit-Ausdrücke durch die vier Zustände (1,0), (√2/3,√1/3), (√1/3,√2/3), (0,1) abbilden. (Das Wurzelzeichen bezieht sich auf den ganzen Bruch.) Diese liegen auf dem Einheitskreis im ersten Quadranten in Schritten von 30° Winkeln.
Das zu codierende Bit-Paar bringen wir wie beschrieben in den Circuit. Die dann anzusetzenden Bit-controlled Gates zeigt die Tabelle.
| Bit-Paar | 00 | 01 | 10 | 11 |
| Binär-Bedingung | 0 | 1 | 2 | 3 |
| Gate | ID | Ry(π/3) | Ry(2π/3) | X |
| Qubit-Zustand | (1,0) | (√2,√1)/√3 | (√1,√2)/√3 | (0,1) |
Für jedes vorgegebene Bit-Paar ergibt sich ein Mess-Ergebnis als Binärzahl, welche die Bedingung definiert, unter der das jeweilige Gate auf das „Speicher-Qubit“ anzuwenden ist. Mit dem Composer lässt sich der Algorithmus wie folgt darstellen (Bit-Paar 11 ist als Input vorgegeben).
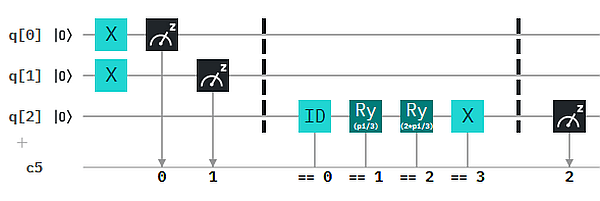 Der erste Teil der „Partitur“ setzt das zu codierende Bit-Paar als Zustand von q0 und q1. Der mittlere Teil versetzt je nach Wert der gemessenen klassischen Bits auf der c5-Linie das Qubit q3 in den entsprechenden Zustand.
Der erste Teil der „Partitur“ setzt das zu codierende Bit-Paar als Zustand von q0 und q1. Der mittlere Teil versetzt je nach Wert der gemessenen klassischen Bits auf der c5-Linie das Qubit q3 in den entsprechenden Zustand.
Wir haben damit 2 Bits in einem Qubit codiert.
Wenn wir es recht überlegen, können wir auf diese Weise eigentlich auch 4, 8 oder beliebig viele Bits in einem Qubit codieren, denn es lassen sich mit Bit-controlled Ry-Gates (cRy) beliebig viele Qubit-Zustände herstellen. Das kling gut – zu gut, um wahr zu sein.
Das ist richtig für den Zustand des Qubits. Und solange wir mit dem Zustand weiter arbeiten im Qubit-Algorithmus, bleibt die Codierung auch erhalten. Wenn wir aber die Codierung rückgewinnen wollen – durch das Auslesen eines Speichers per Messung – bekommen wir lediglich eine 0 oder eine 1! Die Unterscheidung der 4 Zustände in Form von unterschiedlichen Häufigkeiten bekommen wir dagegen nur durch Wiederholungen, etwa 1024 shots. Die unterschiedlichen Zustände des Qubits präsentieren sich nur als Wahrscheinlichkeiten, und die kann man nur verifizieren durch viele Wiederholungen.
Das war der Irrweg. Besser geht’s auf Basis von Verschränkung.
Superdichte Codierung – Verschränkung und Umkehrbarkeit
Der Irrweg war nicht ganz nutzlos. Wir müssen nur das manipulierte Qubit als Teil eines verschränkten Paares sehen. Statt den Algorithmus einfach aus Wikipedia abzuschreiben (wenn man es dort überhaupt versteht), versuchen wir mittels der uns schon bekannten algorithmischen Bausteine den Algorithmus selbst zu konstruieren. Wer keine Lust dazu hat, kann diesen Teil überspringen und gleich mit der Zusammenfassung des Superdense Coding Verfahrens weiter machen.
Eine wichtige Eigenschaft von Qubit-Gates ist noch gesondert hervorzuheben, obwohl sie uns in vielen Beispielen seit der ZBIT-Box schon begegnet ist: Die Reversibilität oder Umkehrbarkeit von Gates und Gate-Kombinationen. In der Qubit-Welt sind außer der Messung, bzw außer Interaktionen mit klassischen Bits, die Operationen umkehrbar. Für jedes Gate und jede Gate-Folge gibt es die Möglichkeit, den Ausgangszustand wieder herzustellen.
Wir wissen z.B. schon, dass zur Umkehrung von X und H die Gates selbst verwendet werden können. Anders ausgedrückt: X—X und H—H ergeben das Gleiche wie das ID-Gate, das den Qubit-Zustand erst gar nicht verändert. Für Drehungen mit Ry gibt es für jeden Drehwinkel einen komplementären Winkel, so dass z.B. Ry(2π/3) durch Ry(-2π/3) wieder aufgehoben wird. Wer Lust hat, kann sich alle bisher erwähnten 1-Qubit Gates noch einmal daraufhin anschauen – auch an Hand der Berechnungsformeln (s. Q10) – oder mit Hilfe von Composer-Tests. Auch Gate-Abfolgen mit controlled Gates wie CNOT (cX) und Tofoli (ccX) lassen sich umkehren. Darunter fällt auch unsere Standard-Verschänkung, Circuit 7 aus Q10, die aus H und CNOT gebildet wird. Die Umkehrung besteht aus beiden Gates in umgekehrter Reihenfolge und löst die Verschränkung wieder auf.
Nun zur Codierung: Wir brauchen ein verschränktes Qubit Paar, statt nur ein Qubit wie oben. Wir erzeugen das mittels H und CNOT aus den Standard-Ausgangszuständen von q0 und q1. Wenn wir nun die 2-Bit Information 00 „codieren“ wollten, müssen wir erreichen, dass sich am Ende bei der Messung auch immer (zu 100%) 00 ergbit. Dieses Ergebnis 00 erfolgt aus der Messung von zwei Qubits im Ausgangszustand. D.h. wir codieren 00, indem wir nach der Verschränkung diese wieder umkehren, also dem H—CNOT ein CNOT—H folgen lassen. Wenn wir wollen, können wir zwischen diesen beiden Circuit-Teilen ein ID-Gate auf die q0-Linie setzen. Damit kann man sagen, das ID-Gate codiert die zwei Bits 00.
Damit hat man die algorithmische Idee für die Codierung von 2 Bits: wir prüfen, welche 2 Bits „am Ende herauskommen“, wenn wir statt ID andere Gates auf die q0-Linie setzen. Das kann man ausprobieren, oder auch errechnen, wie wir es in Q10 getan haben. Tatsächlich finden wir heraus, dass Z, X und die Kombination X—Z die drei anderen 2-Bit-Ergebnisse liefern.
Der Algorithmus in Worten zusammengefasst:
- Es wird ein Qubit Paar in den verschränkten Zustand 1/√2(|00>+|11>) versetzt.
- Ein Qubit wird für die vorgegbenen 2 Bits mit einem passenden Gate „codiert“, das andere Qubit bleibt unberührt.
- Um die codierte 2-Bit Information wieder abzurufen, erfolgt eine Gate-Kombination, die unabhängig ist von der in dem einen Qubit „gespeicherten“ Information. Danach werden beide Qubits gemessen (1 shot).
Im Composer sieht der Algorithmus so aus: (Wir lassen den Teil der Bit-Paar-Bereitstellung weg. Der wäre wie oben davor zu schalten.)
Im ersten Teil wird der schon aus Q9 bekannte verschränkte Zustand zwischen q0 und q1 hergestellt. Im mittleren Teil erfolgt die Codierung auf q0. Dabei steht für jedes der vier 2-Bit Paare eine bestimmte Gate-Kombination (s. folgende Tabelle). Damit ist das Bit-Paar in q0 codiert, ähnlich wie beim ersten Versuch.
Da q0 Teil eines verschränkten Systems ist, kann mit den Gates und Messungen im rechten Teil die Information bei Bedarf wieder ausgelesen werden. Wie schon erklärt, ist die Gate-Kombination die Umkehrung der Gates im Verschränkungsteil.
Mit 1-shot Durchläufen auf dem QC-Simulator können wir diesen Qubit-Algorithmus überprüfen. Im Beispiel ist das Bitpaar 01 codiert. Zur Codierung der 4 möglichen 2-Bit Paare verwendet man im Composer folgende Gates auf q0:
| Bit-Paar | 00 | 01 | 10 | 11 |
| Gates auf q0 | ID | Z | X | X — Z |
Dabei bedeutet X — Z, dass hier X und Z nacheinander angewendet werden. Natürlich kann man den Effekt auch „rechnerisch“ mittels der Zustansabfolge nachweisen.
Wer Lust hat, kann versuchen, diesen Circuit so zu erweitern, dass man, wie im ersten Versuch, den „Bit-Input“ über zwei zusätzliche Qubits und Bit-controlled Gates implementiert. Entweder als Skizze oder im Composer, wenn der Zugang zu IBM Q Experience besteht.
Wenn man diesen Qubit-Algorithmus zum Speichern (und wieder Auslesen) von 2 Bit kritisch betrachtet, wird klar, das eigentlich nicht viel gewonnen ist. Man benötigt zwei Qubits, in verschränktem Zustand, um eine 2-Bit Information „abzulegen“ und gelegentlich wieder auszulesen. Um weitere 2 Bit zu speichern, benötigt man wieder zwei verschränkte Qubits. Der subtile Unterschied liegt lediglich darin, dass nur das eine Qubit die 2 Bit Information per Gates „aufgeprägt“ bekommt, das andere in der Verschränkung unberührt bleibt. Trotzdem gibt es bei der Messung „seinen Anteil“ der 2-Bit Information determiniert aus, hat sich also ggf. verändert. (Mit der Mehr-Qubit GHZ-Verschränkung sieht der Effekt aber schon wieder anders aus. Darauf kommen wir am Ende des Abschnitts Qubit-Kommunikation zurück.)
Plausibler wird der Superdense-Effekt allerdings bei einem anderen Einsatz des Algorithmus, nämlich zur Kommunikation.
Superdichte Codierung – Qubit-Kommunikation
Superdense Coding kann man einsetzen, um z.B. 2 Bit Information mittels eines Qubits zu übertragen, d.h. den Übertragungsaufwand gegenüber bit-weiser Kommunikation zu halbieren.
Auch wenn wir in dieser Blog-Serie die physikalischen Hintergründe vermeiden, muss man sich für das Folgende klar machen, dass es dem Großen Experimentator tatsächlich gelungen ist, verschränkte Qubits einzeln und über getrennte Wege an verschiedene Empfangsstellen zu schicken. Ähnlich, oder sogar mit den gleichen Mitteln, wie wir die klassische Datenübertragung (Internet) kennen. Das geht inzwischen über Hunderte von Kilometern. Wenn also von Qubit Senden die Rede ist, ist das nicht nur eine Fiktion, sondern praktisch realisierbar.
Die Interpretation des Superdense Coding Algorithmus, oben, als Kommunikationsmethode zwischen zwei Teilnehmern, üblicherweise Alice und Bob, ist wie folgt: Alice möchte Bob eine Nachricht (2 Bit) schicken,
- Bob erzeugt eine Verschränkung von zwei Qubits im Ausgangszustand.
- Eines der Qubits schickt er an Alice, das andere behält er.
- —— Erste Trennlinie ——
- Alice möchte 2 Bits an Bob übermitteln. Dazu codiert sie mittels der passenden Gates (s.o.) die 2 Bits in ihr Qubit.
- Anschließend sendet sie ihr codiertes Qubit an Bob.
- —— Zweite Trennlinie ——
- Bob wendet die Gates CNOT und H auf die Verschränkung an
- und misst Alice’s und sein Qubit.
- Bob erhält damit die Nachricht von Alice.
Obwohl hier auch zwei Qubits im Spiel sind, wird nur das eine für die Kommunikation gebraucht. Alice „codiert“ ihre Nachricht an Bob durch Anwendung von Gates auf dieses eine Qubit und schickt es zurück. Das andere Qubit tut nichts. Es ist lediglich Basis für die Verschränkung. Man kann das ganze wiederholen für eine beliebige binär codierte Nachricht, jeweils 2 Bit auf einmal, z.B. zur Übermittlung eines geheimen Schlüssels.
Ohne das hier näher zu erörtern, weist die Qubit-Kommunikation auch gewisse Sicherheitsmerkmale auf. Zum einen kann Alice’s Information nicht gelesen werden ohne das zweite Qubit der Verschränkung. Zum anderen kann die Nachricht nicht „abgefangen“ werden, ohne dass der Verschränkungszustand gestört wird.
Qubit-Kommunikation mit Mehr-Qubit GHZ Verschränkung
Das Kommunikationsverfahren mit zwei verschränkten Qubits lässt sich auf mehrere Qubit-Systeme erweitern. Wir kennen bereits aus Q11 die GHZ-Verschränkung, die eine konsistente Erweiterung unserer 2-Qubit-Verschränkung auf 3 und mehr Qubits ermöglicht. Damit können wir das Verfahren der 2-Bit Übertragung auf mehrere Bit ausdehnen. D.h. wir könnten statt 4 Zwei-Bit-Kombinationen mit einem verschränkten Qubit-Paar mehr Information übertragen, indem Alice z.B. alle außer einem Qubit bekommt und codiert zurück sendet. Wie die Tabelle zeigt,
| GHZ Qubits | 2 | 3 | 4 | 5 |
| # Alice’s Qubits | 1 | 2 | 3 | 4 |
| # Bit-Ketten | 4 | 8 | 16 | 32 |
kann Alice auf zwei Qubits die 8 Bitketten 000, … 111 unterbringen. Die Gate-Kombinationen auf den beiden Qubit-Linien sind allerdings nicht so einfach wie oben. Wir haben 4*4 Gate-Kombinationen, also 16 Möglichkeiten, die 8 3-Bit-Ketten zu codieren. Die Tabelle zeigt, wie das geht (Ergebnisse der 16 Circuits).
| ID | Z | X | X—Z | q0 | |
| ID | 000 | 001 | 010 | 011 | |
| Z | 001 | 000 | 011 | 010 | |
| X | 110 | 111 | 100 | 101 | |
| X—Z | 111 | 110 | 101 | 100 | |
| q1 |
Die Composer-Grafik zeigt als Beispiel einen Qubit-Circuit mit 2 Qubits, die Alice mit q0: Z und q1: XZ codiert hat. Bob bekommt damit die 110.
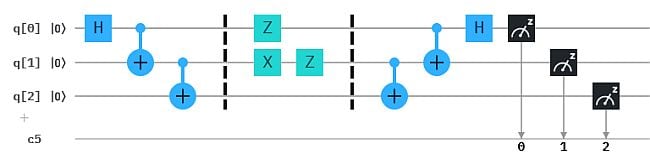 Wie man an der Tabelle sieht, gibt es immer zwei Gate-Kombinationen, die die gleiche 3-Bit-Kette codieren. Alice kann aber alle bereits dadurch abdecken, dass sie für q0 die gleichen 4 Gate-Kombinationen wie oben wählt und für q1 entweder ID oder X.
Wie man an der Tabelle sieht, gibt es immer zwei Gate-Kombinationen, die die gleiche 3-Bit-Kette codieren. Alice kann aber alle bereits dadurch abdecken, dass sie für q0 die gleichen 4 Gate-Kombinationen wie oben wählt und für q1 entweder ID oder X.
Der Verdichtungsfaktor, das Verhältnis Bit-Information zur Anzahl zu codierender Qubits, vergrößert sich mit zunehmender Qubit-Zahl nicht-linear: bei 1 und 2 Qubits ist er 4, bei 3 bereits 16/3 und bei 4 immerhin schon 8.
Hier noch zwei Beispiele für eine 16-zu-3 Codierung: X auf q0, q1, q2 codiert 1000; mit Z statt X auf q1 wird 1111 codiert. Wer Lust hat, kann das mit dem Composer und der 4-Qubit-Verschränkung überprüfen.
Von dieser Stelle aus lassen sich vielfältige Ideen, Experimente und Untersuchungen entwickeln. Zum Beispiel könnten die Qubits an verschiedene Empfänger geschickt werden. Es sei dem eigenem Interesse überlassen, Szenarien hierzu zu überlegen.
Wir legen hier wieder eine Pause ein und vertagen das Thema Quanten-Teleportation auf den nächsten Blog. Eine Kaffepause und etwas Bewegung tun jetzt gut.
Und hier geht es weiter – stay tuned!
Neue Begriffe in diesem Abschnitt:
| Begriff englisch | Begriff deutsch | Bedeutung |
| Superdense Coding | Superdichte Codierung | Codierung von 2-Bit Information in einem Qubit |
| Quantum Communication | Quanten-Kommunikation | Übertragung von (superdichter) Bit-Information durch ein Quantensystem |
| Quantum Teleportation | Quanten-Teleportation | Übertragung eines Qubit-Zustands auf ein anderes Qubit |
| Dependent Gate | Bit-controlled Gatter | Gate, das abhängig von klassichen Bits auf den Qubit-Zustand wirkt |
| If Operator | If-Operator | |
| Reversibility | Reversibilität | Grundsätzliche Umkehrbarkeit von Qubit-Operationen |
| Compression Factor | Verdichtungsfaktor | Verhältnis von Bit-Information zur Anzahl verwendeter Qubits. Z.B. 2 Qubits für 8 3-Bit-Ketten: Faktor 4 |