Die geheimnisvolle Kunst des Teleportierens kennt man – je nach Alter – aus Raumschiff Enterprise („Beam‘ mich hoch, Scotty!“) oder als Zauber aus Harry Potter (Disapparieren und Apparieren). Hier wie da verschwindet etwas oder jemand und taucht an anderer Stelle wieder auf. Der „3D-Druck“ tut im Effekt etwas Ähnliches, nur verschwindet das Original nicht, wenn eine Kopie des Objekts an anderer Stelle „erscheint“. Lediglich die (geometrischen) Daten des Original-Objekts werden an die Empfangsstelle übertragen. Quanten-Teleportation ist beides – oder beides nicht: das Original-Qubit verschwindet und taucht an anderer Stelle als neues Qubit-Objekt auf. Dazwischen wird Information übertragen.
Etwas ernsthafter: Als Quanten-Teleportation bezeichnet man die Übertragung eines Qubit-Zustands mittels klassicher Bit-Information, um ein anderes Qubit in den Zustand des Originals zu versetzen. Dabei geht der Original-Zustand verloren. Und da Qubits keine „Individualität“ haben, hat man vorher und nachher das gleiche Qubit, nur an einem anderen Ort. Teleportation eben. Das funktioniert tatsächlich auch technisch und wurde schon über viele Kilometer hinweg realisiert wie ein Blick ins Wikipedia zeigt.
Die Quanten-Teleportation ist das Gegenstück zur Quanten-Kommunikation (s. Q13): Die Quanten-Kommunikation übermittelt zwei Bit Information mittels eines Qubit-Zustands, die Quanten-Teleportation übermittelt einen Qubit-Zustand mittels zweier Bits. Und in beidem spielt die Verschränkung eine entscheidende Rolle.
Das Teleportationsverfahren schrittweise von der Ausgangssituation her zu entwicklen, wird leicht mühselig, auch für den Leser. Daher schlagen wir dieses Mal den umgekehrten Weg ein: Wir stellen den Algorithmus vor, experimentieren damit ein wenig und liefern die Erklärung weiter unten nach, als systematische Darstellung der Zustandsabfolge.
Teleportation – der Algorithmus
Der Ablauf ist schnell erzählt: Alice möchte Bob den Zustand ihres Qubit (q0) übermitteln. Bob erzeugt dazu ein Qubit-Paar (q1, q2) mit der üblichen Verschränkung (siehe Circuit 7) und schickt das eine davon (q1) an Alice. Das andere verbleibt bei Bob. Alice wendet auf ihre beiden Qubits (q0, q1) zwei Gates an, ein CNOT von q0 zu q1 und danach ein H-Gate auf q0.Anschließend misst sie die Zustände der beiden Qubits. Die beiden Bits aus der Messung schickt sie auf dem klassichen Übertragungsweg an Bob. Der steuert damit ein X- und ein Z-Gate, die auf den Zustand seines Qubits (q2) wirken. Als Ergebnis erhält er q2 in dem Zustand, in dem q0 zuvor war. Wie man das nachprüft, sehen wir anschließend.
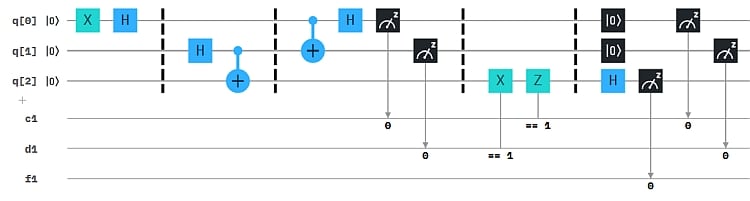
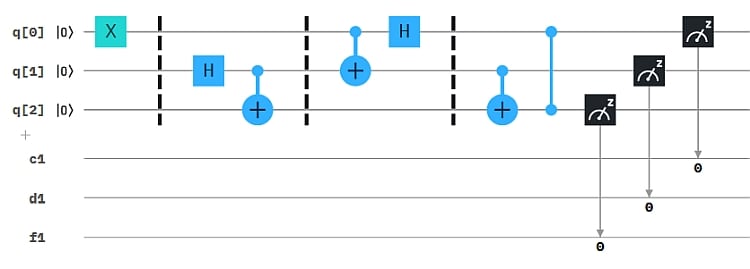
Im Composer sieht die Teleportation wie folgt aus:
 Dieses Composer-Bild hat drei 1-Bit Linien, für jede Qubit-Messung eine. Bisher hatten wir die Messbits von Multi-Qubit-Systemen immer auf einer „Schiene“. Der Vorteil hier ist, dass wir die Messbits unabhängig voneinander zur Steuerung einsetzen können, statt über die 3-Bit Binärzahl-Werte zu steuern. Man sieht das an den bedingten X- und Z-Gates.
Dieses Composer-Bild hat drei 1-Bit Linien, für jede Qubit-Messung eine. Bisher hatten wir die Messbits von Multi-Qubit-Systemen immer auf einer „Schiene“. Der Vorteil hier ist, dass wir die Messbits unabhängig voneinander zur Steuerung einsetzen können, statt über die 3-Bit Binärzahl-Werte zu steuern. Man sieht das an den bedingten X- und Z-Gates.
Die Barrieren (gestrichelte Linien) dienen hier nur zur grafischen Gliederung: Links definiert Alice den Zustand von q0, der teleportiert werden soll. Hier (0,1). Im zweiten Abschnitt erzeugt Bob ein verschränktes Qubit-Paar, wovon er q1 an Alice schickt. Im mittleren Abschnitt wendet Alice auf ihre Qubits ein CNOT und ein Hadamard-Gate an und misst das Ergebnis. Das Ergebnis von q0 wird auf das Bit c1 übertragen, das von q1 auf d1. Alice sendet diese klassichen Bits an Bob. der wendet Bit-controlled Operationen (X, Z) auf sein Qubit an. Wenn der Zustand von q1 als 1 gemessen wird, wird das X-Gate auf q2 angewendet. Wird für q0 eine 1 gemessen, wird das Z-Gate angewendet. Sind beide Messbits 1, dann wirken beide Gates. Abschließend wird q2 gemessen. Wenn alles gut gegangen ist, müsste q2 nun im Zustand (0,1) sein.
Wir starten den Algorithmus und bekommen als Ergebnis z.B. 110 bei einem Durchlauf. Ok, für q2 wird eine 1 gemessen. Die Logik: Wenn q2 nach Teleportation im Zustand (0,1) ist, darf eine Messung keine 0 ergeben. Mit 1024 shots bekommen wir dieses Histogramm:
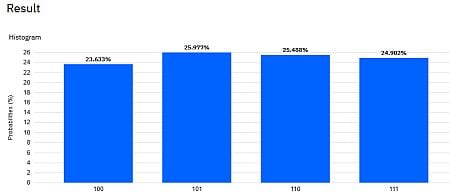 Alle Messergebnisse liefern eine 1 für q2. Interessant ist auch zu bemerken, dass q0 sowohl 1 als auch 0 liefert. D.h. q0 hat seinen ursprünglichen Zustand verloren, der nur das Messergebnis 1 hatte.
Alle Messergebnisse liefern eine 1 für q2. Interessant ist auch zu bemerken, dass q0 sowohl 1 als auch 0 liefert. D.h. q0 hat seinen ursprünglichen Zustand verloren, der nur das Messergebnis 1 hatte.
Wenn Alice q0 im Zustand (1,0) teleportieren will, entfällt das X-Gate am Anfang. Das Ergebnis-Histogramm zeigt, wie zu erwarten, dann nur 3-Bit-Ketten, die links eine 0 haben. Klar!
Damit haben wir die Basiszustände teleportiert.
Teleportation allgemeiner Qubit-Zustände
Wenn wir einen beliebigen Qubit-Zustand als Superposition der Basiszustände (1,0) und (0.1) teleportieren wollen, können wir eigentlich davon ausgehen, dass, wenn diese korrekt teleportiert werden, auch ihre Kombination korrekt in q2 übertragen wird. Wir probieren das gleich mal aus.
Dabei machen wir uns die Darstellung des Messergebnisses von q2 etwas einfacher, indem wir nach der Teleportation q0 und q1 in den Standard-Anfangszustand versetzen und erneut messen. Etwas so:
 Wir setzen statt X das Rotationsgate Ry mit dem Drehwinkel 30° an den Anfang von q0. Eine direkte Messung des Qubits in diesem Zustand ergibt, idealisiert, zu 75% Bit 0 und zu 25% Bit 1. Wir wollen sehen, ob nach Durchlauf des Circuits auch q2 diese Eregbnis liefert.
Wir setzen statt X das Rotationsgate Ry mit dem Drehwinkel 30° an den Anfang von q0. Eine direkte Messung des Qubits in diesem Zustand ergibt, idealisiert, zu 75% Bit 0 und zu 25% Bit 1. Wir wollen sehen, ob nach Durchlauf des Circuits auch q2 diese Eregbnis liefert.
Mit der „Neutralisierung“ von q0 und q1 am Ende des Circuits bekommen wir ein Histogram mit zwei Säulen, die sich nur im Messwert für q2 unterscheiden.
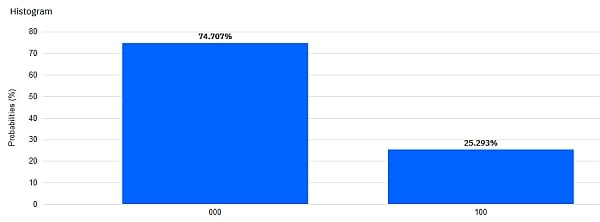 Und wir finden tatsächlich insgesamt etwa 75% der Ergebnisse mit 0 und 25% mit 1 für das linke Bit. Also genau wie erwartet!
Und wir finden tatsächlich insgesamt etwa 75% der Ergebnisse mit 0 und 25% mit 1 für das linke Bit. Also genau wie erwartet!
Qubit Zustände und Messergebnisse
Wir machen das gleiche mit dem Zustand 1/√2(|0>-|1>), der entsteht, wenn wir X — H hintereinander auf |0> anwenden. Wie erwartet, ergibt die direkte Zustandsmessung von q0 das gleiche wie die Messung von q2 nach Durchlauf der Teleportation. Scheint also unsere Vermutung zu bestätigen. Scheint! Wir wollen aber nicht Messergebnisse teleportieren, sondern Qubit-Zustände. Können wir hier aus dem Ergebnis der q2-Messung schließen, dass tatsächlich der Zustand von q0 korrekt auf q2 übertragen wurde? Nein! Ein einfacher Versuch: mit dem Zustand H|0> =1/√2(|0>+|1>) (plus!) bekommen wir die gleichen Messergebnisse. Man kann also nicht sagen, ob die q2-Messung von dem ersten oder dem zweiten Teleportationsbeispiel stammt.
An dieser Stelle müssen wir uns noch einmal klarmachen, dass man zwar immer vom Zustand eines Qubit-Systems auf das Messergebnis schließen kann, aber aus einem Messergebnis nicht eindeutig auf den Zustand zurück schließen kann. Man sagt, die übereinstimmenden Messergebnisse sind eine notwendige Bedingung für die korrekte Teleportation, aber keine hinreichende. Wie können wir hier eine Unterscheidung herbei führen und festellen, ob die Teleportation gelungen ist?
Zwei Möglichkeiten stehen uns zur Verfügung. Erstens, die Abfolge der Zustandsänderungen dieses 3-Qubit-Systems Schritt für Schritt mittels der Formeln nachzuvollziehen und am Ende den tatsächlichen Zustand von q2 mit q0 zu vergleichen. Das „üben“ wir am Ende des Blogs.
Als zweite Möglichkeit nutzen wir die grundsätzliche Umkehrbarkeit von Qubit-Operationen. Wenn wir nach der Teleportation erst noch ein Gate auf q2 anwenden, das das H-Gate umkehrt, und die Teleportation korrekt funktioniert hat, müssten wir im ersten Fall (X — H) immer 1 als das linke Messbit bekommen, im anderen Fall 0. Im Beispiel-Fall ist H selbst ein komplementäres Gate, das wir direkt hinter der letzten Barriere eingefügt haben. (Alternativ könnte man auch Ry(3π/2) verwenden. Mal ausprobieren!) Aus diesen Messergebnissen können wir dann schließen, dass wir in q2 den Zustad |1> bzw. |0> vorliegen haben, und damit der mit H veränderte Zustand korrekt übertragen wurde. Das Umkehr-Verfahren komplementiert also das Messverfahren bei der Bestimmung von Zuständen.
Tatsächlich bekommen wir hier zu 100% die 1 für q2.
Anm.: Natürlich können auch die Basiszustände mit einem Minuszeichen versehen sein, z.B. per 180° Drehung und dabei 0 bzw. 1 als Messergebnis liefern. Dieser Faktor -1 macht aber nichts aus, denn die beiden Zustände im Beispiel unterscheiden sich ja schon über die Messergebnisse.
Teleportieren, Klonen, Kopieren, Übertragen
Warum das doch recht aufwändige Teleportieren, um ein „anderes“ Qubit in den Zustand von q0 zu bringen? Kann man den Zustand nicht einfach kopieren wie bei „gewöhnlichen“ Algorithmen? Beispiel: a = 5, b=a , dann haben wir zwei Variablen mit dem Wert 5 (wie auch immer dies in einer Programmiersprache umgesetzt wird).
Kopieren bedeutet eine Kopie herstellen, d.h. das Original bleibt erhalten, die Kopie ist etwas anderes als das Original. Klonen bedeutet, das Original noch einmal herstellen. Wenn wir den Zustand eines Qubits auf ein zweites Qubit kopieren wollten, würde wir es automatische klonen, denn es gibt nichts, was zwei Qubits voneinander unterscheiden könnte als der Zustand.
Nun gibt es in der Theorie der Qubits ein Theorem, das besagt, dass man Qubits nicht klonen kann, das sog. No-Cloning-Theorem (s. Wikipedia). Das ist nicht zu schwer zu beweisen, überschreitet aber den mathematischen Rahmen, in dem wir uns hier bewegen wollen. Wir müssen also akzeptieren, dass man nicht aus dem (beliebigen, unbekannten) Zustand eines Qubits ein zweites herstellen kann, ohne z.B. das Original zu zerstören. Natürlich kann man, wenn man den Zustand eines Qubits kennt und weiß, wie er „hergestellt“ wurde, ein zweites Qubit mit Hilfe von Gates so präparieren, dass es den gleichen Zustand hat. Dazu muss man aber den Zustand des Originals explizit kennen!
Man kann aber den Zustand eines Qubits übertragen. Teleportation ist eine Methode. Eine ganz einfache Methode ist das Swap-Gate: es vertauscht die Zustände von zwei Qubits in einem Circuit. Man kann das so sehen, dass der Zustand von einem Qubit auf das andere übertragen wird und umgekehrt. In herkömmlichen Algorithmen sieht ein Variablen-Swap zwischen a und b so aus: s = a, a = b, b = s (nicht etwa: a=b, b=a !). Im Effekt haben wir aber nur die Qubit-Variablen getauscht.
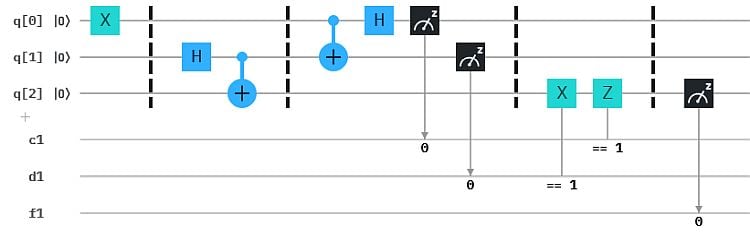
Eine echte Übertragungsmethode ist eine Art lokale Version der Teleportation. Lokal deshalb, weil hierbei keine Übertragung im Sinne eines Transports zwischen entfernten Orten (Alice und Bob) stattfindet. Der Composer-Circuit dazu sieht so aus:
 Das Ergebnis Histogramm entspricht dem ersten oben, d.h. q2 liefert nur 1, die beiden anderen – insbesondere q0 – jeweils 0 und 1.
Das Ergebnis Histogramm entspricht dem ersten oben, d.h. q2 liefert nur 1, die beiden anderen – insbesondere q0 – jeweils 0 und 1.
Statt Bit-controlled Gates wie bei der Teleportation haben wir hier ein CNOT (auch cX genannt) und ein cZ. Damit „kürzen“ wir den Umweg über die Messwerte ab. Statt zu messen, ob q0 bzw. q1 eine 1 oder 0 liefern, und danach die Gates X und Z für q2 zu steuern, nehmen wir gleich die Zustände von q0 und q1, um die Gates zu steuern. Man beachte, dass dabei stillschweigend unterstellt wird, das z.B. Zustand |1> und Messung 1 äquivalent sind.
Der Unterschied zwischen Teleportation und lokaler Übertragung liegt in der „Anwendung“ der Algorithmen. Bei der Teleporation werden Qubits an unterschiedlichen Orten behandelt und die Zustandsübertragung mittels klassicher Bits – und damit klassischer Übertragungsmedien – durchgeführt. Alice kann damit den Zustand eines Qubits, das sich bei ihr befindet, auf ein Qubit von Bob übertragen. Dagegen ist die lokale Übertragung – eben lokal.
Das Zustandsprotokoll
Wenn wir den Teleportationsalgorithmus schon nicht entworfen haben, wollen wir ihn wenigstens verstehen. Dazu versuchen wir die Entwicklung der Zustände des 3-Qubit Systems Schritt für Schritt anhand eines Zustandsprotokolls nachzuvollziehen. Dazu konstruieren wir uns eine Tabelle, die im Wesentlichen die 8 Koordinaten eines 3-Qubit als Spalten hat. Jede Zeile steht für einen Schritt im Algorithmus. Der jeweilige Schritt wird in der Zeile links symbolisch dargestellt. Rechts ist noch Platz für eventuelle Erläuterungen oder Hinweise. Die Zustandskoordinaten der Qubits q2, q1 und q0 werden mit (r,s), (u,v) bzw. (x,y) benannt. Wir wollen das erste Beispiel oben nachvollziehen, beginnen also mit dem X-Gate auf q0.
| (r,s)⊗(u,v)⊗(x,y) | rux | ruy | rvx | rvy | sux | suy | svx | svy | Koordinaten (q2,q1,q0) |
| Ket- / Messbits | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 | Kets / Messwerte (f1, d1, c1) |
| Dezimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Binär-Werte |
| q0: X(1,0)=(0,1) | 1 | q1, q2 sind (1,0) | |||||||
| q1: H(1,0) | 1/√2 | 1/√2 | Hadamard q1 ->1/√2(1,1) | ||||||
| CNOT q1->q2 | 1/√2 | 1/√2 | |||||||
| CNOT q0->q1 | 1/√2 | 1/√2 | |||||||
| q0: H | 1/2 | -1/2 | 1/2 | -1/2 | Hadamard q0 ->1/√2(1,-1) | ||||
| Messung (und Transfer) | 010 | 011 | 100 | 101 | Häufigkeit ca 25% | ||||
| q2: If d1==1 X | 1/2 | -1/2 | 1/2 | -1/2 | Bedingtes X-Gate | ||||
| q2: If c1==1 Z | 1/2 | 1/2 | 1/2 | 1/2 | Bedingtes Z-Gate | ||||
| Messung | 100 | 101 | 110 | 111 | q2 liefert immer 1 |
(Die leeren Felder stehen für 0, bzw. 0 Häufigkeit bei Messungszeilen.)
Wir haben damit am Ende nicht nur die konsistenten Messergebnisse, sondern auch den separierbaren 3-Qubit Zustand (0,1)⊗(1/√2,1/√2)⊗(1/√2,1/√2) mit q2 im Zustand (0,1). Auf ähnliche Weise kann man auch die Teleportation anderer q0-Zustände entwicklen.
Im nächsten Abschnitt werden wir uns mit einem Orakel beschäftigen und einem Algorithmus, der exemplarisch für den Beschleunigungseffekt des „Quanten-Parallelismus“ steht. Doch zunächst die Ergänzung der Begriffstabelle und eine Pause.
Hier geht’s dann weiter – stay tuned!
| Begriff englisch | Begriff deutsch | Bedeutung |
| Barrier | Barriere | Senkrechte, gestrichelte Linie in Composer-Circuit zur Abtrennung von Optimierungsbereichen. Hier nur als Strukturierung verwendet |
| Necessary condition | Notwendige Bedinung | In „wenn A, dann B“: B ist notwendig für A. Zwangsläufige Folge |
| Sufficient condition | Hinreichende Bedingung | In „wenn A, dann B“: A ist hinreichend für B |
| Reversibility method | Umkehr-Verfahren | Methode, das Vorliegen eines Qubit-Zustands zu prüfen unter Verwendung der prinzipiellen Umkehrbarkeit von Qubit-Operationen |
| No-Cloning Theorem | No-Cloning Theorem | Generelles Prinzip, dass Qubits nicht geklont werden können |
| State protocol | Zustandsprotokoll | Schematische Darstellung der Zustandsabfolge eines Qubit-Algorithmus |
| Quantum parallelism | Quanten-Parallelität | Bei Superpositionen wirkt ein Gate auf alle Komponenten der Basis-Zustände „parallel“ |