In diesem Abschnitt wollen wir heraus finden, was es mit Quanten-Parallelismus und der viel zitierten Super-Beschleunigung von Quanten-Algorithmen auf sich hat.  Wir bleiben dabei wieder auf dem Boden der Qubits und werden hier insbesondere wieder von einem Effekt Gebrauch machen, den wir in Q9 schon kennen gelernt hatten, dem (phase) Kickback.

Zur Lösung einer Aufgabe kann es durchaus verschiedenene Algorithmen geben und diese können sich darin unterscheiden, wieviel Aufwand es macht, um die Aufgabe zu lösen. Den Aufwand misst man meist in der benötigten Anzahl von Rechenschritten, Funktionsauswertungen, Entscheidungen usw. und charakterisiert den algorithmischen Aufwand dann in Bezug auf die „Größe“ der Aufgabe. Bei einer Sortieraufgabe kann diese z.B. die Anzahl n der zu sortierenden Dinge sein.

Denken wir uns z.B. ein einfaches „binäres“ Labyrinth. D.h. es gibt einen Eingang, danach gibt es Verzweigungen, bei denen man links oder rechts gehen kann und nach n Verzweigungen kommt man an eine Tür. Alle Türen bis auf eine, dem Ausgang, sind verschlossen. Eine naive Methode, das Labyrinth zu „knacken“ wäre, immer vom Eingang loszulaufen und alle möglichen Wege auszuprobieren, bis man an den Ausgang kommt. Und irgendwann erwischt man ja den richtige Weg. Dieser nicht-so-clevere Algorithmus kann also die Aufgabe lösen. Aber wie hoch ist der Aufwand? Wenn man Glück hat, ist schon der erste Weg der richtige, wenn man Pech hat, der letzte. Also: schlimmstenfalls muss man 2^n Wege ausprobieren.

Orakel und Geheimnisse

Ein Orakel ist etwas, das ein Geheimnis kennt und das man dazu befragen kann. Zum Beispiel das Ergebnis eines WM-Fussballspiels. In der Qubit-Welt wird ein Orakel etwas abstrakter verstanden, als Black-Box oder eine Funktion mit unbekannten Größen (dem Geheimnis), die man durch Berechnung der Funktionswerte (Antworten) für verschiedene Eingabewerte (Fragen) herausfinden will. So kann man  die Aufgabe „Gleichungen mit zwei Unbekannten“ auch als Orakel auffassen, was bei vielen auch im übertragenen Sinne ein ewiges Orakel ist.

Nehmen wir an, es gibt ein Orakel, das den richtigen Weg kennt aber geheim hält. Das Geheimnis ist eine Kette von 0 und 1, wobei 0 für „links abbiegen“ steht und 1 für „rechts abbiegen“. Die Bit-Kette beschreibt damit den Weg vom Eingang bis zur richtigen Tür, dem Ausgang. Wer die 0-1-Kette kennt, kennt den Weg durch das Labyrinth.

Wie kann man diese Bit-Kette herausfinden?

Das erste Orakel

Man könnte alle möglichen n Bit langen 0-1-Ketten aufschreiben und einzeln dem Orakel vorlegen, bis es eine 1 (für richtig) als Antwort gibt. Das entspricht dem Aufwand unserer Wegsuche am Anfang: schlimmstenfalls müssten wir 2^n mal fragen. Der Algorithmus ist naheliegend und klassisch einfach zu beschreiben:

Für alle 0-1-Ketten der Länge n, von 000...0 bis 111...1, 
vergleiche bit-weise mit der geheimen Bit-Kette. 
Zähle die Übereinstimmungen. Sobald eine 0-1-Kette 
n Übereinstimmungen liefert, ist das Geheimnis gefunden. Ende.

Wir gönnen uns hier den Spaß und die Übung, dieses Vorgehen als einen Qubit-Algorithmus mittels Composer darzustellen. Etwa so:

Hier ist n=4 und die vorgelegte 0-1-Kette ist 1011, generiert mittels X-Gates. Das Orakel ist als Qubit-Orakel konstruiert und für uns nicht sichtbar. (Noch nicht. Weiter unten lüften wir die Abdeckung und sehen, wie das Orakel als Qubit-Algorithmus aussieht.) Qubit q4 übernimmt die „Antwort“ des Orakels, das wir durch Messung sichtbar machen. Wenn wir die richtige Bit-Kette als Input vorgelegt haben, bekommen wir hier (zu 100% der Wiederholungen) eine 1 als gemessene Antwort. Für jede andere Bit-Kette dagegen ein „gemischtes“ Messergebnis, d.h. eine Häufigkeitsverteilung über 0 und 1.

Wenn wir in diesem Beispiel alle Inputs ausprobieren, finden wir, dass das Geheimnis 0110 ist. Je nachdem, wie wir vorgehen, kann das maximal 2^n = 16 Versuche bedeuten.

Das zweite Orakel

Eine bessere Möglichkeit ist es, alle Bit-Ketten mit nur einer 1 aufzuschreiben und zu fragen, ob es an gleicher Position auch eine 1 in der geheimen Bit-Kette gibt, also eine Art Filterverfahren.

Für alle 0-1-Ketten, die an nur einer Position eine 1 haben 
und sonst 0, multipliziere jedes Bit mit dem entsprechenden Bit 
der geheimen Bit-Kette und bilde die Summe dieser n Produkte. 
Ist das Ergebnis 0, gibt es an der betreffenden Stelle keine 1 
in der geheimen Bit-Kette, sondern eine 0. Und umgekehrt. 
Sind alle n Positionen durchlaufen, hat man die geheime Bit-Kette 
rekonstruiert.

Auch hier gönnen wir uns den Spaß, statt des klassischen Algorithmus ein Qubit-Orakel zu konstruieren.

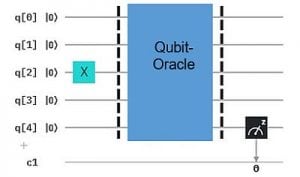Viel Neues ist nicht zu sehen, da wir das Orakel wieder geheim halten. Weiter unten sehen wir, wie einfach der Qubit Algorithmus dazu ist. Hier „prüfen“ wir das 3. Bit des Geheimnisses mit dem Input 0010. Die Messung von q4 liefert eine 1, wenn an der 3. Position eine 1 steht (hier der Fall). Haben wir das X-Gate für alle 4 Qubits verwendet, haben wir alle 4 Positionen in der geheimen Bit-Kette bestimmt.

Es sind also insgesamt nur n=4 „Fragen“ an das Orakel zu stellen, um das Geheimnis aufzudecken – gegenüber 16 beim ersten Algorithmus. Weil 2^n eine Potenz zur Basis 2 ist, bei der n der Exponent ist, spricht man dem zweiten Algorithmus eine exponentielle Verbesserung (Beschleunigung) im Vergleich zum ersten zu: n zu  2^n. Wer sich mit Logarithmen auskennt, kann auch schreiben:  log(n) zu n*log(2).

Beides sind klassische Algorithmen. Das Zweite ist gleichzeitig auch das beste klassische Verfahren, um diese Aufgabe zu lösen. Auch wenn wir sie als Qubit-Algorithmen darstellen, steckt da noch nichts Qubit-Typisches dahinter. Anders wird es mit dem nächsten Verfahren, dem sog. Bernstein-Vazirani-Algorithmus. Der macht u.a. von Superposition und  (phase) Kickback Gebrauch.

Bernstein-Vazirani-Algorithmus

Der Gedanke ist eigentlich ganz einfach: statt das Orakel mit einzelnen Bit-Ketten zu befragen und die Antworten zu notieren, könnten wir doch einen typsichen n-Qubit-Zustand erzeugen, in dem die Zustände |0> und |1> jeweils gleichermaßen vertreten sind, und diesen dem Orakel vorlegen. Das Orakel soll dann entscheiden, „was richtig ist“ –  im Vergleich mit dem Geheimnis.

Zugegeben, ganz so einfach ist es nicht – auch wenn man immer wieder liest, dass ein Qubit „0 und 1 gleichzeitig“ sein kann. Aber wir können als Input für das Orakel die n Qubits mittels Hadamard-Gates in die bekannte Superposition aus (1,0) und (0,1) versetzen. Damit beginnt der Algorithmus, der Bernstein und Vazirani als Entdecker (1992) zugeschrieben  wird. Im Composer mit n=4 sieht das so aus:

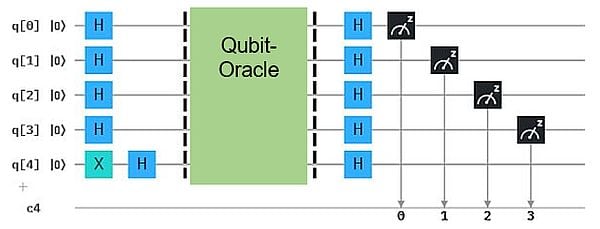
Hier ist q4 wieder ein „Hilfs-Qubit“, das, anders als die Input-Qubits, per X-Gate mit (0,1) initialisiert wird (als Ket: |1>). Wie die geheime Bit-Kette hier im Qubit-Orakel angelegt ist, finden wir gleich heraus. Der Algorithmus bringt also zunächst mittels H-Gate alle Qubits in die Hadamard-Superposition. Am Ende werden die Qubits per H-Gates wieder in Basis-Zustände (1,0) oder (0,1) versetzt und gemessen. Das Hilfs-Qubit ist dabei unwichtig, d.h. auf das H-Gate und die Messung kann man verzichten.

Zum Unterschied zu den klassichen Algorithmen wird dem Orakel hier nicht eine Bit-Kette der Länge n als Input vorgelegt, sondern ein n-Qubit-Zustand! Betonung auf  „Zustand“ und „ein“. Die Antwort des Orakels auf diesen Zustand bewirkt eine Änderung des n-Qubit-Zustands. Werden darauf dann H-Gates angewandt, besteht der Endzustand aus Basis-Zuständen, die durch Messung eine Bit-Kette ergeben. Und diese enstpricht genau dem Geheimnis des Orakels. Kaum zu glauben.

Wenn also die Messung der 4 Qubit-Zustände 0101 ergibt, dann ist das die gesuchte Bit-Kette, die Lösung, der Geheim-Code, der Weg durch’s Labyrinth, oder was auch immer das Geheimnis bedeutet.

Vergleichen wir die Anzahl der Fragen, die wir dem Orakel im stellen müssen, so haben wir beim ersten Algorithmus im schlechtesten Fall 16, beim zweiten immer 4 Fragen zu stellen, und beim Bernstein-Vazirani nur eine. Das Verhältnis zum besten klassischen Algorithmus ist also 1 zu n. Wir haben hier also für große n eine erhebliche algorithmische Verbesserung. In Q16 „Was man so liest“ werden wir die Bedeutung dieses Effektes noch weiter diskutieren. Hier wollen wir zunächst noch verstehen, wie und wodurch dieser Effekt zustande kommt.

Das Orakel und das Phase Kickback

Den zentralen Trick dieses Algorithmus wollen und können wir bereits am einfachsten Problembeispiel verstehen: einer geheimen Bit-Kette der Länge 1. (Dieser Trick ist sehr verständlich dargestellt von M. Treinish in seinem Vortrag „Open Source Quantum Computing“ . Als Youtube video: https://youtu.be/th4TDYX6xoc – 2019, englisch.)

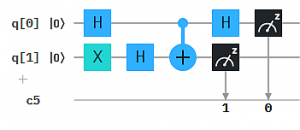In Q9 hatten wir den (Phase) Kickback Effekt schon demonstriert. Das Composer-Diagramm sah so aus (s. Abb. links). Es erinnert, zumindest am Anfang, an das vorige Composer Diagramm, allerdings mit nur einem Input-Qubit und ohne das zweite H-Gate beim Hilfs-Qubit.

Wir haben inzwischen gelernt, die Zustandsänderungen im Algorithmus zu verfolgen, so dass wir den Effekt des Kickback nachvollziehen können. Wir bezeichnen die Koordinaten der Qubit-Zustände von q0 und q1 mit (x,y) bzw. (u,v). Die Ausgangszustände sind (x,y) = (1,0) und (u,v) = (0,1) (nach dem X-Gate).

(u,v)⊗(x,y) ux uy vx vy Koordinaten q1,q0
Kets |00> |01> |10> |11>
(0,1)⊗(1,0) 0 0 1 0
H(0,1)⊗H(1,0)=1/2(1,-1)⊗(1,1) 1 1 -1 -1 (Vorfaktor 1/2)
CNOT q0-q1 (vertauscht uy,vy) 1 -1 -1 1 =1/2(1,-1)⊗(1,-1)
1/2(1,-1)⊗H(1,-1)=1/√2(1,-1)⊗(0,1) 0 1 0 -1 =H(0,1)⊗(0,1)

Der Zustand von q0 ist damit (x,y) = (0,1), der von q1 ist H(0,1), also unverändert. Qubit q1 hat auf diese Weise seinen Ausgangszustand (0,1) auf q0 übertragen (q1 kicked back). DIe Messung für q0 ergibt eine 1. Und das liegt letztlich an dem CNOT. Würden wir dieses weg lassen,  gäbe es die Vertauschung von uy und vy nicht. Die H-Gates auf der q0-Linie würden sich aufheben, der Zustand von q0 bliebe unververändert,  der von q1 bliebe H(0,1). Die Messung von q0 würde 0 ergeben.

In der Ket-Darstellung sehen die Zeilen 4 und 5 wie folgt aus
(|0>+|1>)(|0>-|1>) = |00>-|01>+|10>-|11> —CNOT—  |00>-|01>+|11>-|10> = (|0>-|1>)(|0>-|1>)
Das erinnert an die Binomischen Formeln: Links die 3., rechts die 2. Das CNOT verändert die Dritte in die Zweite.

Jetzt bemerken wir Folgendes:
Eine Kickback-Struktur zwischen Input-Qubit und Hilfs-Qubit wird vom Bernstein-Vazirani-Algorithmus offenbar als 1 erkannt, eine fehlende als 0. Wenn der Algorithmus also eine n lange geheime Bit-Kette  mit Hilfe eines n-Qubit-Zustands erkennen soll, muss man nur entsprechende Kickback-Strukturen (d.h. die CNOT-Gates) hintereinander schalten. Und zwar so, das die Position einer 1 im Geheimnis dem Control-Qubit entspricht.

Hier ist das Beispiel mit „aufgedecktem“ Orakel. Das Geheimnis ist 0101 (oben ist  rechts) und wird korrekt gemessen bei einem Durchlauf mit dem Simulator.

Einsatz eines echten Quanten-Computers: IBMQX2

Bisher haben wir die Qubit-Algorithmen immer auf dem Q-Simulator ablaufen lassen. Zeit für einen echten Quanten-Computer!

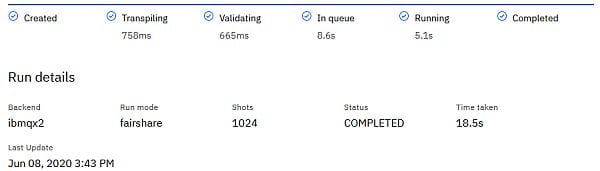
Wir lassen den gleichen Composer Circuit für den Bernstein-Vazirani-Algorithmus nun auf dem IBM-Quanten-Computer IBMQX2 laufen.

Die Anzahl Wiederholungen (number of shots) konnte beim Simulator auf 1 gesetzt werden, da wir erwarten konnten, dass das Ergebnis zu 100% genau eine Bit-Kette liefert. Wird stattdessen ein Quantum-Device verwendet, muss man damit rechnen, dass aufgrund von Dekohärenz-Effekten das Ergebnis eines einzelnen Durchlaufs „gestört“ ist. Mit z.B. n_shots=1024 wird das Programm 1024 Mal wiederholt und man kann aus der Häufigkeit der Ergebnisse die richtige Antwort erschliessen. Es ist, als müssten wir das Orakel mehrfach befragen, weil es die Antwort immer „leicht verwirrt“ gibt. (Ein typischer Diskussionspunkt, wenn es um die (theoretische) „Quanten-Beschleunigung“ geht.)

Hier zunächst das Ablaufprotokoll:

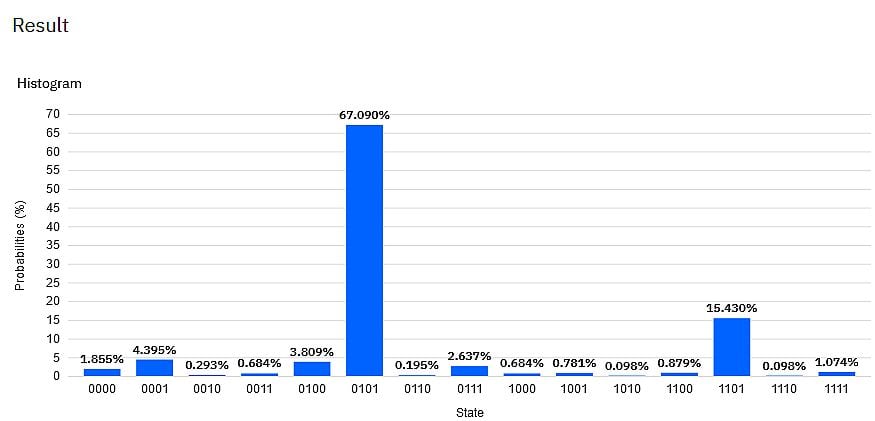
Und hier das Ergebnis der 1042 Durchläufe auf dem ibmqx2:

Wir sehen hier, dass das bei weitem häufigste Messergebnis die Bit-Kette 0101 ist, die wir als gefundenes Geheimnis akzeptieren. Sie stimmt auch mit dem Ergebnis des Simulators überein. Mit geringen Anteilen werden aber auch alle anderen möglichen 4-Bit-Ergebnisse gemessen, ein Effekt, der (zur Zeit) bei echten Quanten-Computern auftritt und kompensiert werden muss. Um diese „Unsicherheit“ zu eliminieren, bleibt uns hier (in dieser Blog-Serie) nur die Wiederholung.

Die ersten beiden Algorithmen „aufgedeckt“

Und da wir gerade dabei sind, decken wir auch die Orakel der beiden klassischen Algorithmen auf:

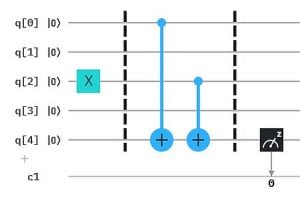Der zweite Algorithmus (blau), der mit n Fragen ebenfalls das Geheimnis 0101 findet. Als Input wird in der Abbildung per q2 das 3. Bit (von rechts) geprüft.

 

 

 

 

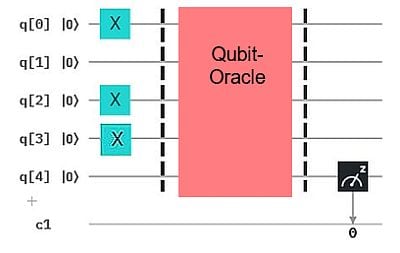
Und hier der erste Algorithmus (pink):Das Orakel des ersten Algorithmus soll ja beantworten, ob die Zustände des n-Qubit-Inputs der geheimen Bit-Kette entsprechen oder nicht. Was wir hier sehen, ist eine naive Methode, diese Antwort über das Hilfs-Qubit q4 zu generieren: Das Orakel „zählt“ die Anzahl der Übereinstimmungen durch „Drehungen“ (cRz – Controlled Rz) des Hilfs-Qubit-Zustands um einen (kleinen) Winkel, hier pi/6. Am Ende wird der Zustand um das n-Fache des Winkels „zurückgedreht“ (Rz-Gate). Waren alle n Inputs „richtig“, führt das Zurückdrehen das Hilfs-Qubit auf den Basiszustand zurück. Ansonsten auf einen Superpostionszustand. Im Beispiel sind die Zustände der Input-Qubits gerade so, dass alle mit der im Orakel angelegten Bit-Kette 0110 übereinstimmen. Das Messergebnis (wiederholte Durchläufe) ist 1 zu 100%.

(Anm.: Das Rz- und cRz-Gate haben wir bisher nicht behandelt, weil wir im Wesentlichen ohne dem auskommen. Wir kennen das Z-Gate. Rz und Controlled Rz erzeugen winkelabhängig „Teilschritte“ von Z in Form von Drehungen. Um sie in unserem Circuit wirksam zu machen, müssen wir vorher den Basis-Zustand von q4 mit dem H-Gate transformieren – und am Ende rück-transformieren. Etwas kompliziert, aber es funktioniert. Alternativ kann man auch ein „controlled Ry“ durch eine Kombination von mehreren Gates implementieren, was hier aber unnötig unübersichtlich würde.)

Wie geheim ist geheim?

Im Composer Diagramm zum Bernstein-Vazirani Algorithmus scheint es zunächst etwas unsinnig, das Orakel zu befragen, wenn die „geheime Bit-Kette“ im Circuit-Teil für das Orakel doch ganz offensichtlich ist: 1, wo ein CNOT angelegt ist, 0 sonst.

Zum einen ist es immer so, dass, wenn man eine Übereinstimmung von zwei Dingen prüfen will, beides irgendwie „zur Verfügung“ haben muß. So auch, wenn man eine unbekannte Bit-Kette durch Inputs herausfinden will. Auch die unbekannte Bit-Kette muß „irgendwie“ verfügbar oder überprüfbar vorliegen. Die Form kann beliebig kompliziert sein oder so einfach wie eine klassische binäre Daten-Variable – oder eben ein Teil eine Qubit-Circuits.

Zum anderen kann man sich vorstellen, dass der Orakel-Teil des Circuits „unerkannt“ implementiert wird, etwa durch einen Algorithmus außerhalb des eigentlichen Bernstein-Vazirani-Circuits. In der Qubit-Programmierumgebung Qiskit kann man z.B. in einer Funktion eine zufällige Bit-Kette erzeugen, die dann in einen Programmblock für das Orakel umgesetzt wird. Damit ist das Orakel innerhalb des Gesamt-Algorithmus eine Black Box.

Generieren eines zufälligen Orakels – mit Qiskit

Wir zeigen und erklären zum Abschluss diese Aufgabe für eine unbekannte, zufällige Bit-Kette der Länge n= 32 anhand eines vollständigen Python Programms unter Verwendung der Qiskit-Umgebung. Der Algorithmus wird also insgesamt in einer Programmiersprache beschrieben, statt umgangssprachlich oder grafisch per Composer Diagramm. Die Qiskit Ausdrücke entsprechen den Komponenten eines Composer Circuits; man kann sich sogar das Qiskit Programm als Composer Grafik anzeigen lassen. Python/Qiskit Programme kann man am besten als sog. „Notebooks“ direkt in der IBM Q Experience Cloud entwerfen und ausführen – auf dem QC-Simulator oder einem realen QC. (Notebooks sind eine Kombination aus Text- und Programm-Teilen. Man kann also im Klartext die „Story“ zum Programm in einzelnenen Schritten aufschreiben und dazu die Programm-Teile einfügen. Alles zusammen ist dann ablauffähig. Die Dateiendung der Notbooks ist .ipynb – für iPython NoteBook.) Zum Testen von Teilen oder einzelnen Ideen kann man immer auch auf den Composer zurückgreifen, denn die „Übersetzung“ eines Composer Circuits nach Qiskit ist simpel.

Wir empfehlen hiermit auch den Übergang vom Composer (grafisch) zu Qiskit/Python (Programmierung). Mit Qiskit/Python ist man viel flexibler in der Formulierung von Qubit-Algorithmen. Außerdem kann man damit gut die Kombination von konventioneller Algorithmik und Qubit-Algorithmik gestalten, d.h. den Quanten-Computer nur für seine speziellen Stärken einsetzen.

Unter diesem Link: “ Bernstein-Vazirani-Algorithmus“ kann man das komplette Notebook als html-Datei herunterladen bzw. ansehen. Möchte man mit dem Notebook im IBM-Q Umfeld experimentieren, kann man die Datei in der IBM-Q Umgebung in ein leeres Qiskit-Notebook hineinkopieren (Text-Zellen getrennt von Code-Zellen).

Hier beschreiben wir nur die wesentlichen Teile in Text-Form.

  • Defintion eines Qubit-Systems namens ‚circ‘  mit n=33 Qubits und Mess-Bits
    • 32 für das Geheimnis und 1 Hilfs-Qubit
  • Die Gates werden je Qubit eingesetzt
    • X-Gate für das Hilfs-Qubit q[32]: circ.x(q[32])
    • H-Gate für alle Qubits von q[0] bis q[32]: circ.h(q[i])
  • Das Geheimnis wird generiert und das Orakel eingefügt
    • Zufällige 0-1-Kette (das Geheimnis) wir erzeugt
    • Für alle Positionen s mit 1 in der Kette wird das entsprechende Qubit mit einem CNOT versehen: circ.cx(q[s],q[32])
  • Die Gates je Qubit werden ergänzt
    • H-Gate für alle Qubits von q[0] bis q[32]: circ.h(q[i])
  • Mess-Operation
    • Messen der Zustände der Qubits: circ.measure(q,c)
    • c enthält die Bit-Ergebnisse (von rechts nach links)
    • Das c-Bit ganz links gehört zum Hilfs-Qubit und wird ignoriert
  • Das Qubit-Programm wird ausgeführt
    • Die „Backend-Maschine“ wird aufgerufen (Simulator oder ein realer Quanten-Computer)
    • Die Anzahl Wiederholungen (’shots‘) wird festgelegt: n_shots=1
    • Das Programm wird gestartet: job=execute(circ, ….)
    • Das (Mess-)Ergebnis wird erstellt: result=job.result()
  • Das Ergebnis ‚result‘ wird aufbereitet
    • Die Ergebnis-Bit-Kette wird als Lösung des Geheimnisses ausgegeben.

Ein Beispiel für die Ergebnis-Ausgabe des Programms:

Anm.: Ergebnisse für Qubits q0 bis q32 werden in der Bit-Kette von rechts nach links geschrieben
      Qubits, die nicht gemessen werden, haben den Messwert 0 per Default

counts:  {'100101100111110100101111010110000': 1}
Gefundenes Geheimnis: 00101100111110100101111010110000
Das Orakel war: [0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0]

Mit diesem Ausflug in die Qiskit-QC-Programmierung öffnen wir das Feld für weitere, neue Versuche, Qubit-Algorithmen zu entwerfen, zu realisieren bzw. nachzubauen. Es sei aber noch einmal daran erinnert, dass die Qubit-Welt über das, was wir hier dargestellt haben, hinaus noch weitere mathematische Begriffe und Methoden kennt und verwendet. D.h. nicht alle Algorithmen, die sich in der Literatur oder in Einführungs-Videos finden, sind mit unserer „Schul-Qubit-Toolbox“ realisierbar oder verstehbar.

Im nächsten Abschnitt der Blog-Serie wollen wir versuchen zu verstehen, was so alles in den Medien und populärwissenschaftlichen Beiträgen zum Quanten-Computing geschrieben wird. Zu „Was man so liest“ geht es hier.

Zum Schluss wieder die Tabellen-Ergänzung mit neuen Begriffen:

Begriff englisch Begriff deutsch Bedeutung
Oracle Orakel Black box, Qubit-Funktion mit (unbekannten) Parametern
Secret Geheimnis (Unbekannte) Parameter des Orakels, meist Bit-Ketten
Exponential improvement Exponentielle Verbesserung Auch als „Beschleunigung“ bezeichnet. Aufwand eines Algorithmus im Vergleich zu einem anderen im Verhältnis log(n) zu n, wobei n die „Größe“ des Problems kennzeichnet. Auch n zu 2^n.
Number of shots Anzahl Wiederholungen Wiederholungen eines Durchlaufs, um eine statistische Verteilung über die möglichen Messergebnisse (Bit-Ketten) zu erhalten
Decoherence Dekohärenz Ungesteuerter Zerfall von (Mehr-)Qubit-Zuständen auf einem realen physikalischen Gerät (Quanten-Computer)
ibmqx2 ibmqx2 Realer Quanten-Computer, offen zugänglich in der IBM Q Cloud
Rz, cRz Rz, cRz Weiteres Gate bzw. Controlled Gate mit Rotationswirkung
Qiskit Qiskit Q-Bibliothek zur Einbettung in (z.B.) Python. Professionelle Alternative zur grafischen Programmierung mit dem Composer
Notebook Notebook Skripte kombiniert aus aus Text- und Programm-Teilen (Zellen)
Cells Zellen Notebook-Abschnitte, die Text oder Programm-Code enthalten und einzeln oder zusammen ausgeführt werden können
Ancillary Qubit Hilfs-Qubit Extra Qubit, das für den Algorithmus gebraucht wird aber nicht in das (Mess-)Ergebnis eingeht

 

Print Friendly, PDF & EmailBeitrag Drucken