Die gute Nachricht: Das ZBIT-Modell in der x-y-Koordinatendarstellung ist bereits das QBIT-Modell. Allerdings beschränkt auf 8 Zustände. R, X, H und M sind mit ihren Formeln dazu passend definiert. Mehr noch, man kann jeden Punkt (x,y) auf dem Einheitskreis als Zustand gelten lassen und die Operatoren liefern wieder einen gültigen Zustand. Und auch die Doppelt-Anwendung von X und H auf ein (x,y) liefert diesen Zustand wieder. (Wer Lust hat, kann regelrecht nachrechnen, dass HH(x,y) = (x,y) liefert und das gerne ins Kommentarfeld eintragen).
Eine ganze Reihe von Qubit-Algorithmen kann man bereits mit diesem ZBIT-Modell formulieren. Wer daher keine Lust hat, sich mit der Erforschung einer weiteren Box des Großen Experimentators zu befassen, kann daher auch zu Q8 über Qubit-Sprachgebrauch und Multi-Qubit-Modelle übergehen. Die nicht so gute Nachricht: Man verpasst dann die Möglichkeit, (x,y)-Zustände außer den 8 ZBIT-Zuständen zu entdecken. Mit dem ZBIT-Modell können wir keine Zustandsüberführung durchführen, die aus dem 8er-Set herausführt.
QBIT-Box

Dieses Mal konfrontiert uns der Große Experimentator mit einer ganz mysteriösen Box. Schwarz wie die Nacht (ohne Mond und Sterne) mit nichts auf den Flächen. Keine Touch-Felder, keine Klappe, keine Aufschrift ist zu erkennnen. Was sollen wir mit dieser Box anfangen, wie sie erforschen, wie damit experimentieren?
Nach längerem Überlegen und Probieren kommen wir auf die Idee, die Box mal ins Gefrierfach zu legen und zu kühlen. Nach kurzer Zeit hat sie sich tatsächlich verändert und sieht so aus:
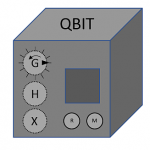
Die Box ist nun grau und zeigt die Aufschrift QBIT, hat die üblichen beiden Touchfelder X und H und zusätzlich eine Art Touch-Drehrad mit der Kennzeichung G, einer Skala und einer Markierung am Rand. Es gibt keine Klappe, die man auf und zumachen könnte. Dafür aber ein umrahmtes quadratisches Feld mit zwei Touch-Feldern M und R darunter. Wir vermuten gleich, dass das M für „Messen“ steht, also dem früheren „Klappe auf“, und R für „Reset“, das offenbar „Klappe zu“ ersetzt. Was das Drehfeld bedeutet, müssen wir wohl experimentell herausfinden.
Nach einiger Zeit in Zimmertemperatur verschwinden die Strukturen auf den Flächen wieder und die Box sieht aus wie vor der Kühlung. Da hat sich der Große Experimentator wohl eine besondere Schikane ausgedacht? Wir müssen also vor jedem Experiment die Box hinreichend tief kühlen, das erschwert Untersuchung und die Überprüfung unseres Modell-Ansatzes. Egal, da müssen wir durch. Vielleicht hilft ja eine Cool-Box ein wenig.
QBIT-Box Experimente
Wir überprüfen zunächst das Naheliegende – immer im gekühlten Zustand. Die Touch-Felder R, X, H und M bewirken das Entsprechende wie bei der ZBIT-Box:
R —- M -> Dunkel, d.h. das quadratische Anzeigefeld wird schwarz
R —- X —- M -> Licht, das Anzeigefeld wird hell.
R —- H —- M -> Dunkel und Licht jeweils mit der Häufigkeit ungefähr 1/2
Kombinationen, wie X—H und H—H zeigen ebenfalls die von der ZBIT-Box bekannten Ergebnisse.
Neu ist das Touch-Drehrad G. Wir machen ein paar Versuche in Serie bei gleicher Einstellung. Dazu hilft die Skala am Rand. Wenn wir genau hinsehen, unterteilt die Skala den gesamten Kreis so ähnlich wie ein Ziffernblatt der Uhr. Allerdings haben die 12 Teilstriche noch Punkte jeweils auf der Mitte dazwischen. Ein Viertel des Umfangs hat damit 6 Markierungen, die analog zu einer Halbstunden-Skala sind. Im 360º Kreis entspricht das 15º. Wir bemerken, dass der „Zeiger“ immer auf „3 Uhr“ zurückspringt, wenn wir R betätigen, also scheint „3 Uhr“ so etwas wie die Ausgangsposition des Dreh-Feldes zu sein.
Wir drehen den Zeiger auf „12 Uhr“ bzw. 90° gegen den Uhrzeiger-Sinn (also mathematisch positiv) und berühren anschließend das „G“ in der Mitte des Drehfeldes. Als Messergebnis leuchtet das Anzeigefeld hell. Wir wiederholen diese Operation mehrfach:
R —- G90 —- M -> L
und bekommen immer L. Nun liegt nahe, was wir, mehr oder wenniger systematisch, ausprobieren – immer mit ein paar Wiederholungen. Wir finden:
R —- G45 —- M -> Dunkel und Hell, vermutlich jeweils mit der Häufigkeit ungefähr 1/2
R —- G00 —- M -> Dunkel – das wußten wie schon, denn das ist genau das RM-Experiment von oben.
R —- G30 —- M -> D und L, mit einem Weiß/Schwarz-Häufigkeitsverhältnis von etwa 1:3.
R —- G135 — M -> D/L im Verhältnis etwa 1:1, also gleiches Ergebnis wie mit G45.
R —- G180 — M -> Dunkel für die Stellung „9 Uhr“, also genau gegenüber der Ausgangsposition.
Mühselig, wie es sein mag, die Box muss systematisch erforscht werden. Wir machen die Experimente mit G für jeden der 12 Drehfeld-Teilstriche in Serie, 50 mal, und notieren die Häufigkeiten von Hell und Dunkel für jede Position. Die Grafik zeigt die Häufigkeit von Hell als Punkte über die 12 Teilstriche von „3 Uhr“ bis „3 Uhr“.
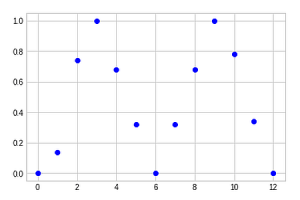
Ein gewisses Muster ist zu erkennen, wenn auch spärlich. Machen wir das Ganze noch einmal für die Zwischenpunkte und tragen die in eine Gesamt-Grafik mit 24 Positionen ein.
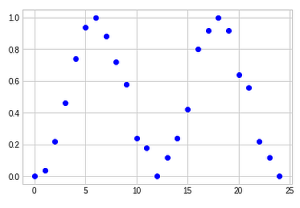
Man erkennt, dass die Punkte, die die Häufigkeit von L im Experiment zeigen, über die verschiedenen Dreh-Feld Einstellungen periodisch sind. Bei 12, d.h. „9 Uhr“-Stellung, ist die Häufigkeit wieder 0, bei 2 und 18 sind die Werte 1. Soweit man die trigonometrischen Funktionen kennt (sin, cos), kann man hier eine Art sin-Funktion erkennen. Da die Werte aber immer zwischen 0 und 1 liegen, sieht es eher nach sin² aus über 0 bis 360º, in 24 Schritten.
Bevor wir weitere Experimente machen, wollen wir versuchen, das Bisherige zu verstehen, d.h. uns ein passendes QBIT-Modell zu machen, das auch die Operation von G berücksichtigt.
Ein QBIT-Modell
Wir hatten in Q6 für das ZBIT bereits ein konsistentes Modell entwickelt und eine Darstellung gefunden, die uns Zustandsübergänge und die Zustand-Output Beziehung „rechnerisch“, d.h. durch Formeln, zu formulieren ermöglichten. Die Zustände liegen dabei auf einem Einheitskreis in der x-y-Ebene.
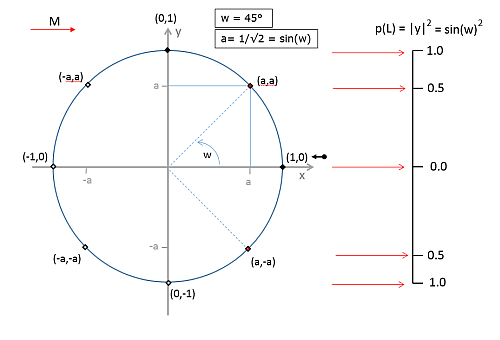
Für das QBIT-Modell müssen wir die Dreh-Operationen berücksichtigen. Die Einstellungen von „3 Uhr“ (entspricht 0º) bis „12 Uhr“ (entspricht 90º) liefern Ergebnisse für die Häufigkeit von L, die sich aufsteigend von 0 bis 1 verteilen. Von 90º bis 180º (9 Uhr) geht es umgekehrt von 1 nach 0. Und bei Einstellungfen von 180º bis 360º wiederholt sich das Geschehen. Wenn wir uns die p(L) Linie in der ZBIT-Modell Grafik ansehen, heißt das eigentlich nur, dass die experimentellen Ergebnisse auf der p(L)-Linie von der Mitte nach oben, dann nach ganz unten und zurück zur Mitte bewegen. Jeder Punkt auf der p(L)-Linie hat aber eine Entsprechung auf dem Einheitskreis – genauer, sogar zwei! (Mit zwei Ausnahmen.) Wir können daher als die Zustände eines QBIT-Modells alle Punkte auf dem Einheitskreis nehmen. Das umfasst natürlich auch automatische die 8 Zustände aus dem ZBIT-Modell.
Damit bekommen wir als QBIT-Modell-Beschreibung eine Erweiterung des ZBIT-Modells:
- Die Zustände sind alle Punkte auf dem Einheitskreis, d.h. alle (x,y), für die x² + y² = 1 gilt.
- Die Output-Werte bilden das Intervall [0,1], interpretiert als Wahrscheinlichkeiten p(L) für das Messergebnis L.
- Ein Zustand (x,y) ergibt als Output M(x,y) = |y|² = p(L) (wobei hier die das Betrags-Symbol | | unnötig ist). p(D) ist entsprechend x² = 1-y².
- R(x,y) = (1,0) und liefert p(L) = 0
- X(x,y) = (y,x). Wir leiten daraus ab, dass der Output M nach Anwendung von X p(L) = |x|² ergibt.
- H(x,y) = 1/√2(x+y,x-y). Was ist der Output p(L) direkt nach Anwendung von H auf (x,y)? (Wer Lust hat, usw.)
Wie beschreiben wir die Dreh-Feld Operation G? G „dreht“ den Ausgangszustand (1,0) auf dem Einheitskreis entsprechend dem“Dreh-Winkel“ (G für Gyro). Dazu müssen wir etwas mathematisch ausholen. Ein Zustand auf dem Einheitskreis (x,y) kann auch durch den Winkel w zum Ausgangspunkt beschrieben werden. Nämlich – da der Radius des Einheitskreises 1 ist – als x = cos(w) und y = sin(w). Damit hat der Modell-Zustand, der durch Drehen um den Winkel w ausgehend vom Zustand (1,0) erreicht wird die Koordinaten (x,y) = (cos(w),sin(w)). Die erfüllen die Gleichung für den Einheitskreis, klar, und das |y|² ist gleich sin(w)². Also setzen wir
- G(w) = (cos(w),sin(w)), wobei w der Dreh-Winkel von (1,0) aus ist.
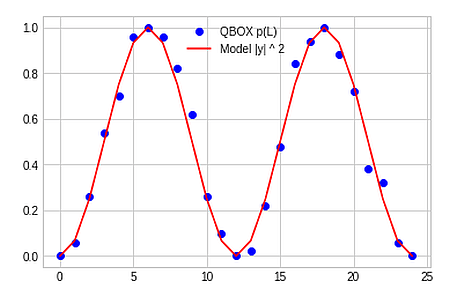
Wir können damit das Modell einfach berechnen und den Output, das p(L), für alle Drehfeld-Einstellungen von 0 bis 360 in die Grafik der experimentellen Ergebnisse einzeichnen. Die rote Linie repräsentiert die Funktion sin(w)² und passt (zumindest visuell) hervorragend zu den blauen Punkten. Wir haben damit eine „statistische Bestätigung“ unseres Modells.
Vorhersagen und Erklärungen
Was passiert, wenn wir zwei G hintereinander schalten?
1. R —- G90 — G45 —- M -> 0.5 (Modell), 49:51 Experiment
2. R —- G45 — G90 —- M -> 0.5 (Modell), 52:48 Experiment
3. R —- G60 — G45 —- M -> 0.93 (Modell), 4:96 Experiment (D:L)
4. R —- G105 — M -> 0.93 (Modell), 9:91 Experiment (D:L)
Offenbar ist der Effekt zweier Drehungen der gleiche wie eine Drehung um die Summe der Winkel, in der Theorie wie – statistisch – im Experiment.
Wir wissen, dass X so wirkt, dass die Koordinaten vertauscht werden.
5. R —- G60 —- M -> 0.75 (Modell), 22:78 Experiment (D:L)
6. R —- X —- G60 —-M -> 0.25 (Modell), 74:26 Experiment (D:L)
7. R —- G60 —- X —-M -> 0.25 (Modell), 75:25 Experiment (D:L)
Das X vor oder nach der Drehung vertauscht die Koordinaten und damit die theoretischen Wahrscheinlichkeiten für D und L.
Nun noch ein paar Kombinationen mit H:
8. R —- G60 —- H —- H —- M -> 0.75 (Modell), 24:76 Experiment (D:L)
Das entspricht dem Ergebnis von Versuch 5. D.h. das doppelte H hebt sich auf – wie wir das ja schon aus dem ZBIT-Modell kennen. Aber was macht ein einzelnes H?
9. R —- G60 —- H —- M -> 0.067 (Modell), 93:7 Experiment (D:L)
Vorhersage und Experiment passen recht gut zusammen. Wir können aber das Ergebnis aus dem Modell „errechnen“, indem wir die Formeln anwenden.
Die Drehung des Ausgangszustands (1,0) um 60º liefert den Punkt
(cos(w),sin(w)) mit w=60º
auf dem Einheitskreis. H bedeutet, darauf die Formel 1/√2(x+y,x-y) anzuwenden, also
H(cos(w),sin(w)) = 1√2(cos(w)+sin(w),cos(w)-sin(w)).
Dieser Zustand wird gemessen (in Serie von 100). Mit M bedeutet das
p(L)=|y|²=1/2*(cos(w)-sin(w))².
Das ergibt (berechnet z.B. mit Wolfram Alpha) p(L) = 0.0669. Die Modell-Zustände, -Übergänge und -Outputs kann man berechen – die Ergebnisse der QBIT-Box dagegen NICHT!
10. R —- H —- G60 —- M -> Liefert in Experiment-Serien Ergebnisse um 8:92 für (D:L). Das sieht aus wie das Ergebnis von 3., oben.
Ob das stimmt, können wir per Modell herausfinden. R setzt den Anfangszustand (1,0), H macht daraus 1/√2(x+y,x-y)=1/√2(1,1), das kennen wir schon. Dieser Punkt liegt auf dem Einheitskreis mit dem Winkel 45º, da die x- und y-Koordinate gleich sind. D.h. H macht mit (1,0) das Gleiche wie eine Drehung um w=45º. Anschließend „dreht“ G60 weiter auf 45+60=105º. Und das ist genau das, was wir in Versuch 3. hatten. Damit ist das theoretische Ergebnis wieder p(L)=0.93, passend zum Experiment. Aber Achtung! H ist nicht generell mit G45 gleich zu setzen. H ist keine Drehung um einen festen Wert. Wo H(x,y) liegt, hängt von (x,y) ab. Wer Lust hat kann überlegen, was passiert, wenn wir nach R erst ein X einsetzen (und das in einen Kommentar schreiben).
Auf diese Weise kann man viele weitere 1-Qubit Algorithmen formulieren und per Modell untersuchen. Leider ist der Gegenstand unsere Experimente nur ein virtueller. Der G.E. hat uns keine Handhabe gegeben, Experimente anders als immer mit der gleichen Routine zu machen: Kühlen, Reset, Operationen anwenden, Messen und das Ergebnis im Hell/Dunkel-Feld beobachten. Protokollieren und Statistik machen. (Wer wissen will, wie die Ergebnisse der obigen Mess-Serien zustande gekommen sind, kann das im nächsten Blog-Abschnitt kennen lernen.)
Die Vielfalt der Bezeichnungen
Eines hat in der Abfolge der Modellierungsansätze vermutlich irritert: die offensichtliche Beliebigkeit der Darstellung und Bezeichnung der Modell-Zustände. Nun, das hatte einen guten Grund. Es sollte zeigen, dass es
(a) verschiedene Modell-Beschreibungen für die gleiche Sache gibt,
(b) keine davon per se die „Wahre“ ist und
(c) es der „Sache“ egal ist, welche Beschreibung wir wählen, sofern sie nicht im Widerspruch zu den Experimenten steht.
Wir können daher bei der Modellwahl auf andere Eigenschafte achten, z.B. ob die Begriffe leicht zu verstehen oder zu merken sind, ob man damit leicht operieren bzw. rechnen kann, oder ob uns eine der Möglichkeiten einfach mehr Spaß macht, besser „in der Hand liegt“.
In der Qubit-Algorithmik findet man daher mindestens 3 Standard-Beschreibungsansätze für Qubits. Wir werden darauf später teilweise noch eingehen können.
Zunächst wollen wir aber mal in unserem eigenen Zoo von Modellen Klarheit schaffen, vom BIT bis zu QBIT. Dazu zeigt folgende Tabelle, welche Zustandsbezeichnungen in den verschiedenen Ansätzen sich entsprechen.
| Uhr | Grad | π | π/2 | x-y-KoS | p(L) | ZBIT | BIT | Alice | Qubit |
| 3:00 | 0º | 0 | 0 | (1,0) | 0 | [00] | [0] | Alice | |0> |
| 2:00 | 30º | 1/6 | 1/3 | (√3/2,1/2) | 1/4 | — | — | — | |
| 1:30 | 45º | 1/4 | 1/2 | (1/√2,1/√2) | 1/2 | [01] | — | Charly | |+> |
| 1:00 | 60º | 1/3 | 2/3 | (1/2,√3/2) | 3/4 | — | — | — | |
| 12:00 | 90º | 1/2 | 1 | (0,1) | 1 | [11] | [1] | Debbie | |1> |
| 9:00 | 180º | 1 | 2 | (-1,0) | 0 | — | — | — | |
| 6:00 | 270º | 3/2 | 3 | (0,-1) | 1 | — | — | — | |
| 4:30 | 315º | 7/4 | 7/2 | (1/√2,-1/√2) | 1/2 | [10] | — | Bob | |-> |
| hh:mm | wº | φ | θ | (x,y) | |y|² | — | — | — | x|0>+y|1> |
Jede Spalte entspricht einer der Beschreibungsmöglichkeiten, die Einträge in einer Zeile entsprechen einander. Die erste Spalte zeigt Werte unseres Uhren-Bildes, mit dem Ausgangszustand auf 3 Uhr. Die zweite Spalte zeigt die entsprechenden Werte in Grad, gegen den Uhrzeigersinn. Statt Grad-Angaben kann man auch den Kreis mit Winkelangaben in π kennzeichnen. Die Spalte x-y-KoS gibt die entprechenden Koordinaten wieder, p(L) die zugehörige Wahrscheinlichkeit für L. Im ZBIT- und BIT-Modell hatten wir nur 4 bzw. 2 Zustände gekennzeichnet. Für das ZBIT die Zustände sogar mal mit Namen gekennzeichnet. Die letzte Spalte und die Spalte π/2 sind Zustandsschreibweisen, die wir noch kennen lernen werden. Sie gehören zu den erwähnten Standard-Beschreibungen für Qubits. Wenn man mal nicht weiß, was was ist, hat man hier eine Tabelle zum Nachschlagen.
Die letzte Zeile stellt die verwendeten Symbole für einen allgemeinen Zustand in der jeweiligen Schreibweise dar. Es fällt auf, dass es für das ZBIT- und BIT-Modell keinen „allgemeinen“ Zustand gibt. Es sind stets die 4 bzw. 2 Zustände und nichts „dazwischen“.
Wir sind jetzt in der Qubit-Welt angekommen, zumindest in einer der Qubit-Welten. Mit einem Qubit kann man algorithmisch recht wenig anfangen, vergleichbar einem Programm mit nur einer Variablen. Interessanter werden Qubit-Algorithmen, die mehrere Qubits umfassen – in einem sog. Qubit-Register. Das werden wir – nach einer kleinen Pause natürlich – im nächsten Abschnitt kennen lernen. Und zwar durch kleine praktische Beispiele von der Art „Hello Qubit World“ in Q2, ausgeführt auf dem IBM Q Experience Quantencomputer (bzw. dem Simulator).
Hier geht’s weiter.
Ach ja, wofür steht wohl QBIT auf der Box? Vorschläge gerne in den Kommentarfelden.
