Q8 Fingerübungen - Einfache Qubit Algorithmen ausprobiert

Wir wissen nun, was ein Qubit ist. Genauer, wie man ein Qubit modellieren kann – aber wir wollen uns ein wenig sprachliche Vereinfachung zugestehen, solange wir uns darüber im Klaren sind. Fassen wir noch einmal zusammen:

Ein Qubit ist ein Konstrukt, das einen Zustand hat, der durch Operatoren  beeinflusst wird, und der über ein Messverfahren einen binären Wert liefert (Bit). Der Zustand ist aus einer kontinuierlichen (unendlichen) Menge.  Wiederholte Messungen bei gleichem Zustand liefern eine Häufigkeitsverteilung über die binären Werte, die man als Wahrscheinlichkeitsverteilung dem Zustand zuordnen kann.

Wir legen fest, dass die Operatoren den Zustand determiniert beeinflussen, mathematisch also eine Abbildung darstellen. D.h. gleicher Operator angewendet auf gleichen Zustand liefert gleiches Ergebnis (neuer Zustand). Für das Messverfahren gilt das natürlich nicht. Wohl aber für die Zuordnung der Wahrscheinlichkeitsverteilung zu einem Zustand.

In diesem Sinne ist ein klassisches Bit auch ein Sonderfall eines Qubits. Wieso?

Für die konkrete Beschreibung von Qubits verwenden wir (einfache) mathematische Ausdrücke: Die Zustände beschreiben wir durch die Koordinaten (x,y) eines Punktes auf dem Einheitskreis in der x-y-Ebene. Die binären Messwerte bezeichnen wir mit 0 und 1. Für die Punkte, die einen Zustand repräsentieren, verwenden wir gelegentlich „Namen“ anstelle der Koordinaten; das macht manchmal das Lesen einfacher. Insbesondere sind folgende Bezeichnungen in der Qubit-Welt üblich: |0> für (1,0), |1> für (0,1) – also für die Punkte des Einheitskreises, die auf den positiven Koordinatenachsen liegen. (Diese Zustände hatten wir beim ZBIT-Modell mit [00] und [11] bezeichnet. Die etwas ungewöhnliche | >-Schreibweise erklären wir später. ) Damit kann man einen Zustand (x,y) auch als Kombination von |0> und |1> schreiben:  x|0> + y|1>.

Ein typischer Sprachgebrauch in der Qubit-Welt ist z.B. „das Qubit |1>“ an Stelle von  „das Qubit im Zustand |1>“.  Kein Problem, wenn klar ist, was gemeint ist. „Namen“ für die Qubits sind wie herkömmliche Variablen-Namen zu verstehen und werden in den Composer-Grafiken links vor die zugehörige Linie gestellt. Sie sind der Einfachheit halber durchnummeriert. Entweder als q0, q1, usw. oder im Stile von Python-Listen als q[0], q[1] usw., also mit eckigen Klammern.

Ein weiterer häufig anzutreffender Begriff für die x-y-Kombination der beiden Basiszustände ist „Superposition„, übersetzt als „Überlagerung“, von |0> und |1>. Ein leicht mysteriös klingender Begriff für die Kombination der beiden Zustände. Der stammt aus der Physik und wird in der Mathematik übrigens Linearkombination genannt.

Wie wir in Q7 gesehen haben, ist für x|0> + y|1> dann |y|²  die Wahrscheinlichkeit p(1) für den binären Wert 1 bzw. |x|²=1-|y|² die für 0 bei der Messung des Qubits in diesem Zustand.

Man kann damit den Messvorgang, genauer, den wiederholten Messvorgang, auch als einen Operator darstellen, der Zustände (x,y) in Häufigkeiten von Bits überführt:

M(x,y) = M(x|0> + y|1>) = ( |x|², |y|²).

Bei Mehr-Qubit-Zuständen wird das, wie wir sehen werden, eine hilfreiche Darstellung. Wir bezeichnen M nicht als Gate, weil wir Gates für Übergänge von Zustand zu Zustand reservieren wollen, ( |x|², |y|²) aber kein Qubit-Zustand ist, sondern Wahrscheinlichkeiten für Bit-Ergebnisse.

Woher wissen wir, in welchem Zustand sich ein Qubit befindet? Man wählt |0> als Ausgangszustand, herstellbar durch die Operation R. Wenn wir anschließend weitere Operatoren anwenden, liefert jeder einen determinierten Folgezustand. Wenn wir die Wirkung der Operatoren berechnen können, wie in Q7 für X, H usw., können wir die Zustände nachverfolgen, wissen also bei der Messung, welcher Zustand vorliegt – auch wenn die Messung selbst nur ein Bit (0 oder 1) liefert. Dies ist ein wichtiges Prinzip, um Algorithmen für Qubits formulieren zu können.

1-Qubit Beispiele

Das wollen wir im Folgenden für einige erste kleine Beispiele mit einem bzw. zwei Qubit(s) tun und diese gleich auch auf einem Qubit-Computer realisieren.

Für einen Qubit Computer (physikalisch oder als Simulator) müssen wir fordern, dass wir die physikalischen Entsprechungen der Qubit-Operatoren so konstruieren können, dass sie – in wiederholten Messungen –  Häufigkeiten eines binären Ergebnisses liefern, die der Wahrscheinlichkeit von 0 und 1 in dem Operator-generierten Zustand entprechen. Klingt kompliziert, ist es auch. Aber wir machen nichts falsch, wenn wir darauf vertrauen, dass die Quantencomputer-Konstrukteure dafür gesorgt haben.

In Q7 u.a. hatten wir schon einige 1-Qubit Algorithmen in der Form R — X — H — M oder ähnlich formuliert. Diese Schreibweise kommt der grafischen Darstellung im „Composer“ (Komponisten) der IBM Q Experience Umgebung schon sehr nahe. Wir probieren es einfach und lassen die „Partitur“ vom Simulator ausführen. (Wie man Zugang zur IBM Quantencomputing-Umgebung bekommt, wird in diesem Blog beschrieben. Besser noch, man findet es selbst heraus. Hier ist der Link zum IBM Q Login.) Es ist wirklich zu empfehlen, diese Erfahrung „in echt“ zu machen (s. Q2). Statt des Simulators kann man zur Ausführung auch einen der verfügbaren echten Quantencomputer auswählen!

1. R— X — H — M

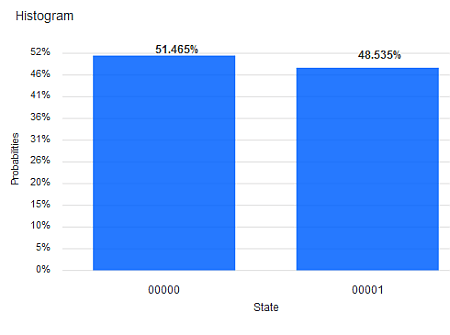
Das Ergebnis zeigt die Häufigkeiten von 0 und 1 (interpretiert als klassische Bits) bei einer Serie von 1024 Durchläufen.  Die Legende der State-Achse ist für die gleichzeitige Messung von 5 Qubits ausgelegt, daher die 5-stelligen Bit-Ketten. Das Bit rechts kommt aus der Messung des Qubit Nr. 0, dem obersten im Composer, wenn wir mehrere Qubits haben. Dass die Achse mit „state“ (Zustand) bezeichnet wird, ist etwas verwirrend. Gemeint ist bestenfalls der „Ausgabezustand“.

Nicht ganz zufällig gibt es die hier schon verwendeten Operatoren X und H auch beim Qubit-Composer. Im Qubit-Sprachgebrauch werden die Operatoren Gates genannt, zu deutsch Gatter. Die Gates werden auf Wires (Leitungen) positioniert. Und die „Partitur“ wird  in der Qubit-Welt Circuit (Schaltung) genannt. Am Anfang eines Qubit-Wire ist das Qubit auf den Ausgangszustand |0> gesetzt. Das Symbol (Gate) dafür im Composer ist nicht R sondern einfach |0>. Die beiden Gates auf dem Wire von Qubit q[0] heißen X-Gate oder NOT-Gate, weil es den Qubit-Zustand umkehrt,  und Hadamard-Gate (H-Gate), benannt nach dem französichen Mathematiker J. Hadamard. Die Wirkung hatten wir in Q7 bereits formelmäßig definiert.

Als ein anderes Beispiel nehmen wir aus Q7 „Vorhersagen und Erklärungen“ die Nummer 8.

2. R —- G60 —- H —- H —- M

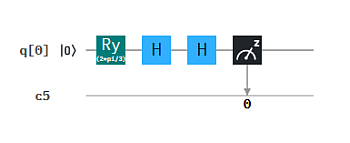
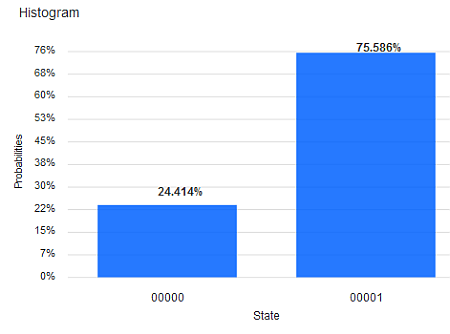
Es fällt auf, dass wir bei der QBIT-Box das Dreh-Feld mit G bezeichnet haben, im Composer aber ein neues Gate Ry(2*pi/3) verwendet haben. Mit G hatten wir in Q7 den Dreh-Operator vereinfacht. So wie wir G definiert hatten, entspricht dem das Rotations-Gate Ry mit dem Paramterwert θ=2*pi/3. Man sieht in der Tabelle am Ende von Q7, dass dieses θ dem Winkel w=60º entspricht. (Die Gates in den Composer- bzw. Programmier-Umgebungen orientieren sich an einer anderen Zustandsbeschreibung, die dazu führt, dass der Winkel, den wir für Drehungen auf dem x-y-Einheitskreis definieren, in der Composer-Beschreibung verdopplet werden muss.)

3. R — G30 — X — M vergleichen wir mit R — G30 — M, um die Wirkung von X zu verifizieren. Hier müssen wir, wie eben erklärt, für G30 das Gate Ry mit pi/3 parametrisieren. Wir verzichten dabei auf die Histogramme und notieren stattdessen nur die Häufikeiten der Messergebnisse.

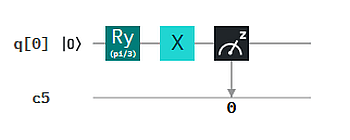
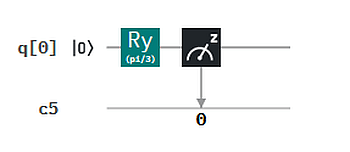
Man sieht also sehr schön den Effekt eines X-Gates aus der wiederholten Messung: Es vertauscht die Zustandskoordinaten. Für die Basis-Zustände ergibt sich daraus: X: |0> -> |1>, d.h. (1,0) -> (0,1), und umgekehrt. Wir merken an, dass wir hier wieder von den Messergebnissen (Bits) auf den Zustand (Qubit) nach Anwendung der Gates schließen. Die Messergebnisse sind nicht der Zustand!

4. R — Gw — M. Das Diagramm der QBIT-Box Experimente in Q7 (blaue Punkte) ist natürlich auf diese Weise (3b) entstanden! Das w durchlief alle Werte von 0º bis 360º (das entspricht θ=2*pi) in 15º-Schritten. Für jedes w wurde ein Cirquit der Form 3b) erzeugt, der jeweils 50 Mal durchlaufen wurde. Die Häufigkeiten von 1 (das entspricht dem L) wurden in die Grafik eingetragen. Das Ganze wurde natürlich in Form eines kleinen (Python-)Programms durchgeführt. Im Kern einer Schleife über die verschiedenen Winkel steht dabei das Python-Pendant zum Composer Circuit:

## Circuit definieren 
q_box = QuantumCircuit(q, c) 
rot = k*2*pi/m 
q_box.ry(rot,q) 
q_box.measure(q[0], c)

Etwas ausführlicher wird das Programm in einem Kommentar zu diesem Blog gezeigt.

2-Qubit Beispiele

Bevor wir uns theoretisch mit Zwei- und Mehr-Qubit Kombinationen befassen, probieren wir einfach einmal ein paar Beispiele mit dem Composer praktisch aus. Wir müßten dazu natürlich auch unsere einfache Schreibweise für Qubit-Algorithmen erweitern, etwa zwei Zeilen untereinander. Das stimmt aber ziemlich genau mit den Composer Grafiken überein, die wir bereits in Abschnitt Q2 erkundet hatten. Daher formulieren wir die kleinen Algorithmen gleich als Circuit.

5. Probieren wir es mal mit

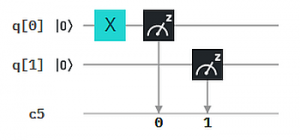und versuchen zu verstehen, was wohl als kombiniertes Messergebnis herauskommen wird. Der Ausgangszustand von Qubit 0 (q0-Wire) wird mit X zu |1> und dann gemessen. Qubit 1 (q1-Wire) wird sofort gemessen, bleibt also im Zustand |0>. Grundsätzlich gibt es 4 mögliche Messergebnisse, nämlich die vier 2-Bit Kombinationen 00, 01, 10, 11. Das Ergebnis hier ist natürlich 100% 01.

Zur Erinnerung (an Abschnitt Q2): Auf der c-Linie kommen die Messergebnisse an – in Form von klassischen Bits (c für classical). Die 5 deutet an, dass die c-Linie die Ergebnisse von bis zu 5 Qubits aufnimmt (s. Histogram nächstes Beispiel), auch wenn wir hier nur 2 Qubits verwenden.

6. Etwas schwieriger:

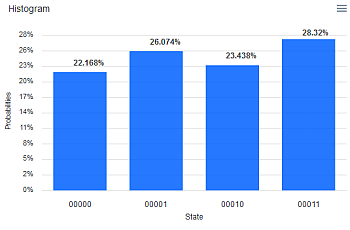
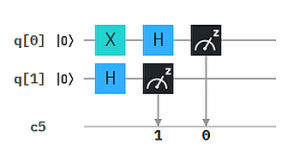Hier wird q0 zunächst geswitcht und dann mit dem Hadamard-Gate transformiert. D.h. |0> wird zu 1/√2 (|0> – y|1>), oder in Koordinaten wie in Q7 zu 1/√2(1,1). Die Wahrscheinlichkeiten für 0 und 1 als Messergebnis sind damit 1/2. Für q1 wird nach H der Zustand 1/√2 (|0>+y|1>) gemessen, was die gleichen Wahrscheinlichkeiten für Qubit 1 ergibt. Was ist also das Gesamtergebnis (1024 „shots“)?

 

 

 

 

Hier zählen nur die zwei rechten Bits, so dass also die experimentellen Häufigkeiten um den zu erwartenden Wert 0.25 schwanken. (Die Konvention ist, das Bit-Ergebnis von q0 immer ganz rechts zu schreiben.)

7. Das Hello Qubit World Beispiel aus Q2 sah als „Partitur“ so aus:

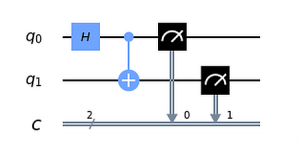Hier finden wir nach dem H ein neues Gate, das offenbar zwei Qubits miteinander in Beziehung bringt. Das ist das Controlled-Not-Gate, auch als CNOT oder CX bezeichnet. Es beeinflußt q1 – da, wo das + im Kreis steht – in Abhängigkeit vom Zustand des Qubit q0. Genauer: wenn q0 im Zustand |1> ist, kehrt sich q1 um – hier also von |0> nach |1>. Ansonsten bleibt der Zustand von q1 unverändert, also hier |0>.

Schauen wir uns das Ergebnis an (1024 shots).

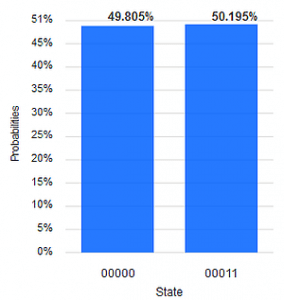Das Histogramm zeigt nur positive Werte für die 2-Bit Messergebnisse 00 und 11, zu jeweils ziemlich genau 50%. Die beiden anderen, 01 und 10, kommen bei Messungen nicht vor.  Das hat verschiedene Konsequenzen, auf die wir später noch eingehen werden. Hier stellen wir erst einmal fest, dass das CNOT-Gate offenbar die beiden Qubits „gleichschaltet“. Aber Achtung – nur bezüglich der Messergebnisse! Beide sind nach diesem Circuit entweder 0 oder 1, und was, das bestimmt q0. Um über die Zustände zu sprechen, müssen wir wieder unser Modell bemühen.

Damit können wir das Ergebnis noch besser verstehen: durch das Hadamard-Gate geht der q0-Zustand in die Kombination von |0> und |1> über, jeweils mit Anteil 1/√2. Daher ergibt sich der neue Zustand von q1 nach der CNOT-Regel als Kombination von |0> (unverändert) und |1> (verändert) mit den entsprechenden Anteilen von 1/√2. Und q1 kann nur 0 ergeben, wenn sein Zustand sich nicht geändert hat, also wenn q0 das Ergebnis 0 liefert. Andernfalls hätte sich q1 umgekehrt und würde 1 liefern. Das erklärt – in Worten – warum 01 und 10 nicht als Messergebnis auftreten können. Im nächsten Blog werden wir das „nachrechnen“.

Die „Gleichschaltung“ der beiden Qubits durch diesen Circuit bedeutet u.a., dass wir wissen können, welchen Messwert das andere Qubit hat, wenn wir nur das eine gemessen haben. Wir können aus einer Messung das Ergebnis beider Messungen erschließen! Das wirkt zunächst einmal ungewöhnlich und führt zu teilweise „geheimnisvollen“ Deutungen. Doch davon später.

Ein kleiner Ausflug: Die Wires sind so etwas wie die „Lebenslinien“ der beiden Qubit-Variablen q0 und q1. Sie beginnen beide in einem Anfangszustand und „enden“ durch Messung. Mit etwas Phantasie kann man auch klassische Algorithmen als Composer Diagramm darstellen.

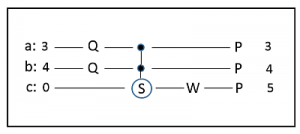
Zum Beispiel kann man die Berechnung der Hypothenusenlänge nach dem Satz des Pythagoras a²+b²=c² so in Composer-Form darstellen. Dabei sind a,b,c die Variablen, 3 ,4, 0 die Anfangszustände, Q ist die Quadrat-Operation, W die Wurzel, und das Konstrukt in der Mitte mit dem S auf dem c-Wire ist die Summenbildung der Variablen auf den beiden oberen Wires im aktuellen Zustand. Die Messoperation ist hier P, für print. Auch hier „beobachtet“ man nur die Anfangszustände und die print-Ausgaben. Noch enger ist die Analogie, wenn man sich das P „destruktiv“ vorstellt,  d.h. die Variablen werden nach Ausgabe „gelöscht“ oder auf Null gesetzt. Insgesamt also eine schöne Algorithmen-Analogie zum Verständnis der Composer-Diagramme.

An dieser Stelle ist erst einmal wieder eine Pause fällig. Wir haben Beispiele für kleine 1- und 2-Qubit Algorithmen untersucht und mittels Quantencomputer-Simulator praktisch ausprobiert. Außerdem haben wir zwei neue Gates kennen gelernt: als Entsprechung für unser G (Dreh-Feld) bei der QBIT-Box das Ry-Gate und das CNOT, das zwei Qubits verbindet. Und eine ganze Reihe neuer Begriffe, die im Sprachgebrauch der Qubit-Algorithmik verwendet werden. Es ist wieder hilfreich, sich eine tabellarische Übersicht zu machen und im weiteren Verlauf zu ergänzen. Der Anfang sei hier gemacht.

Begriff englisch	Begriff deutsch	Bedeutung
Composer	Composer	Tool bzw. Form zur grafischen Darstellung von Qubit-Algorithmen
Circuit	Schaltkreis	Qubit-Algorithmus
Wire	Wire (Leitungen)	Algorithmische „Lebenslinie“ eines Qubits
Gate	Gatter	Qubit-Operator in einem Algorithmus
Paramter	Parameter	Gates wie Ry können eine Parameter haben, z.B. einen Drehwinkel.
|0>, |1>, |a>	|0>, |1>, |a>	Schreibweise für Qubit-Zustände, alternativ zu Koordinaten
Basis	Basiszustand	Hier |0> oder |1>
Superposition	Überlagerung	(Linear-)Kombination von Qubit-Zuständen, meist von |0> und |1>
Hadamard-Gate	H-Gatter	Spezieller Superpositionsoperator
M Operator	M Operator	Mess-Operator, berechnet aus Qubit-Zuständen Wahrscheinlichkeiten von Bit-Ergebnissen
Classical Bit	Klassisches Bit	Messergebnisse werden als Bits / Bit-Ketten ausgegeben
c-Wire	c-Wire	Wire, das die Messergebnisse aufnimmt (Bit-Ketten)
Initial State	Anfangszustand	Jedes Qubit beginnt im Zustand |0>
Ry-Gate	Ry-Gatter	Eine bestimmte Art der Drehung, vergleichbar mit dem G im ZBIT-Modell
shots	shots	Anzahl Durchläufe eines Algorithmus für Ergebnis-Statistik

 

Bevor es nun weiter geht mit  Mehr-Qubit Registern, werden wir noch einige verblüffende Besonderheiten des Circuits aus Beipiel 7 untersuchen.

Stay tuned! Hier geht’s weiter.