Die Corona-Krise, ihre Bewertung und die Maßnahmen zu ihrer Bewältigung sind seit Wochen das alles beherrschende Thema in den Medien. Dabei kommt neben den medizinischen, biologischen, wirtschaftlichen, gesellschaftlichen, rechtlichen und ethischen Fragen, die das Virus aufwirft, auch die Mathematik ins Spiel. Es sind mehrere Themenkomplexe, bei denen die Mathematik gefragt ist und adressiert wird: bei der Statistik der Datenerfassung und –auswertung, bei der Modellierung der Ausbreitung und der Ausbreitungsgeschwindigkeit der Infektionen, aber auch bei der Modellierung der wirtschaftlichen Auswirkungen des Shutdowns. Ferner spielen u.a. Methoden des Maschinellen Lernens bei der Suche nach einem Impfstoff oder nach Medikamenten eine wesentliche Rolle.
Wir wollen hier nur den Komplex der Ausbreitung der Infektionen ansprechen. In den Medien spielt dabei das Modell des exponentiellen Wachstums eine besondere Rolle. Außer von Virologen und Epidemiologen hören wir es von Vertretern aller Medien und von Politikern. Mathematiker kommen in der Öffentlichkeit kurioserweise kaum oder eher am Rande zu Wort.
Zur Charakterisierung der Ausbreitung der Infektionen werden in den Medien eine Vielzahl von Kurven gezeigt, oft erstaunlich nichtssagende Kurven, deren Sinn von Laien nicht und Experten nur mit Mühe verstanden werden können. Manche der Kurven werden in einem Achsenkreuz gezeigt, ohne dass die Achsen bezeichnet oder erläutert würden, so dass nicht klar wird, was die Kurven eigentlich veranschaulichen.
Zum Beispiel wurden in der anfänglichen Berichterstattung in den Medien zur Erklärung, warum eine Verlangsamung der Virus-Ausbreitung (durch Isolierung, Kontaktreduktion, soziale Distanzierung) medizinisch sinnvoll und notwendig ist, oft jeweils zwei Kurven gezeigt, deren Form an „Normalverteilungen“ aus der Statistik erinnern (eine spitze und eine flache Kurve). Zu diesen Kurven wird erklärt, dass sie einerseits die schnelle, ungebremste Ausbreitung (die spitze Kurve) und andererseits eine systematisch verlangsamte, zeitlich gedehnte Ausbreitung der Infektionen (die flache Kurve) beschreiben. Dabei soll eine waagerechte Linie, unter der die flache Kurve verläuft, die Kapazitätsgrenze für Intensivbehandlungen in deutschen Krankenhäusern charakterisieren. Diese Kurven haben aber keine präzise bezeichnete mathematische Bedeutung, sondern eher symbolischen Charakter.
Um etwas mehr Klarheit in die Vielfalt der Darstellungen zu bringen, wollen wir hier ein paar allgemeine Worte über „mathematische Wachstumsmodelle“ sagen. Dabei wenden wir uns ganz bewusst an den mathematisch nicht besonders versierten oder interessierten Leser.
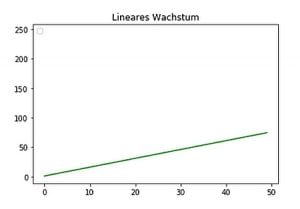
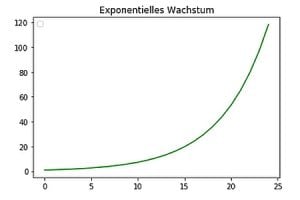
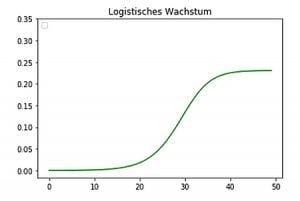
Die drei wichtigsten Wachstumsmodelle sind das lineare, das exponentielle und das logistische Modell. Um sich einen Eindruck, eine Idee dieser drei Modelle zu verschaffen, braucht man nur einen Blick auf die Form der zugehörigen Wachstumskurven zu werfen:
Von diesen drei Modellen ist das lineare Wachstumsmodell das einfachste und alltäglichste. Trotzdem gehen wir hier zunächst auf das Modell des exponentiellen Wachstums ein, weil von diesem seit dem Beginn der Corona-Krise in den Medien fast ausschließlich die Rede ist.
Exponentielles Wachstum ist eigentlich leicht zu verstehen: Wenn sich z.B. irgendeine Menge täglich verdoppelt, dann haben wir es mit exponentiellem Wachstum im engsten Sinne zu tun. Sich vorstellen kann man das ja sofort. Verblüffend ist aber, wie schnell die Menge nach einer eher ruhigen Startphase anwächst.
Veranschaulicht wird dieses Anwachsen gern durch die indische Legende vom Schachbrett mir den Reiskörnern. Bei Verdoppelung der Anzahl der Reiskörner von einem Feld des Schachbretts zum nächsten sieht das Wachstum am Anfang harmlos aus. Aber am Ende, nachdem alle 64 Felder belegt sind, übersteigt die Menge der Körner alle Vorstellungen. Allein auf dem letzten Feld müssten die Reisernten der ganzen Welt von vielen hundert Jahren untergebracht werden.
Eine andere Geschichte, das Gleichnis vom Lilienteich, soll die Bedrohlichkeit des exponentiellen Wachstum deutlich machen: In einem Teich wächst eine Linie täglich auf die doppelte Größe an. In den ersten Tagen ist die Ausbreitung scheinbar völlig bedeutungslos, so geht es weiter, und auch am 29.Tag ist „nur“ der halbe See von Lilien bedeckt. Aber dann, am 30. Tag, ist der See vollständig zugewachsen, und alles Leben im See erstickt…
Nun muss es bei exponentiellem Wachstum nicht eine tägliche Verdoppelung der betreffenden Menge sein, es kann auch ein anderer Zeitraum sein, der zu einer Verdoppelung führt, z.B. eine Verdoppelung alle 4 Tage oder alle 10 Tage.
Nur am Rande sei erwähnt, dass wir es z.B. bei der Zinsesverzinsung von Kapital (wenn die Zinsen nicht abgeschöpft, sondern dem Kapital hinzugefügt werden) ebenfalls mit exponentiellem Wachstum zu tun haben: Bei einem Jahreszinssatz von zum Beispiel 5 % würde sich das Kapital bei Zinsesverzinsung ungefähr alle 14 Jahre verdoppeln.
Die Situation verändert sich aber grundlegend, wenn der Zeitraum, in dem die Verdoppelung stattfindet, nicht konstant ist, sondern sich laufend verändert. Wenn also z.B. der Verdoppelungszeitraum erst 4 Tage, dann – nach einigen Wochen – nur noch 6 Tage, dann – noch einige Wochen später – vielleicht nur noch 10 Tage beträgt usw.
In einem solchen Fall, wenn der Zeitraum, in dem die Verdoppelung stattfindet, sich dauernd verändert (vergrößert), haben wir es nicht mehr mit exponentiellem Wachstum im engeren Sinne zu tun, sondern mit einem möglicherweise deutlich komplizierteren Anwachsen. Über einen größeren Zeitraum betrachtet, sieht das Wachstum dann vielleicht eher wie lineares Wachstum aus. Konkret: Wenn sich der Zeitraum, in dem die Verdoppelung stattfindet, ebenfalls verdoppelt, also von 4 auf 8 Tage, dann auf 16, danach auf 32 Tage usw. anwächst – dann ist das global gesehen kein exponentielles, sondern lineares Wachstum.
Lineares Wachstum lässt sich schnell abhandeln: Es wird durch eine gerade Linie charakterisiert. Es ist das uns vertrauteste Wachstumsmodell: Der Preis einer Ware steigt in der Regel linear mit der Menge der Ware, der Arbeitslohn sollte linear mit dem Zeitraum anwachsen, in dem die Arbeit ausgeübt wird usw. Bei allem, was wir in der Schule und im Alltag mit dem Dreisatz-Prinzip ausgerechnet haben und ausrechnen können, haben wir es mit linearen Beziehungen, mit linearem Wachstum zu tun.
Logistisches Wachstum als alternatives Modell zu exponentiellem Wachstum
Wie im Beispiel der Schachbrettlegende wächst unbegrenzt exponentielles Wachstum schließlich dramatisch schnell an, es geht sehr schnell ins quasi „Unendliche“.
In der Wirklichkeit ist exponentielles Wachstum aber nur theoretisch unbegrenzt, es geht praktisch eigentlich immer in eine andere Form des Wachstums über. Neben dem gerade behandelten einfachen linearen Wachstum ist ein sehr wichtiges, besonders realistisches Wachstumsmodell das logistische Wachstum.
Die obige Kurve zum logistischen Wachstum zeigt (von links nach rechts) das Charakteristische des logistischen Wachstums: Zu Beginn, in der Startphase, verhält sich die Kurve wie beim exponentiellen Wachstum, ändert dann aber – an einem „Wendepunkt“ – ihre Richtung, wird flacher und nähert sich immer mehr einer waagerechten Geraden an. Das Wachstum wird durch diese Gerade begrenzt. In der Realität ist der Übergang vom exponentiellen Wachstum in begrenztes Wachstum in aller Regel dadurch bedingt, dass Ressourcen beschränkt sind und aufgebraucht werden…
Auch auf die Corona-Ausbreitung bezogen, haben wir es langfristig mit logistischem Wachstum zu tun: Wenn die senkrechte Achse die Gesamtzahl aller Infizierten (einschließlich der bereits Genesenen) beschreibt, ist klar, dass weitere Infektionen spätestens dann ausgeschlossen sind, wenn alle Individuen infiziert sind oder waren (und eine zwei- oder mehrmalige Infektion ausgeschlossen ist). Nach den Erkenntnissen der Epidemiologie ist sogar zu erwarten, dass eine solche Begrenzung praktisch schon erreicht wird, wenn etwa 70% der Individuen infiziert sind oder waren. (Man spricht dann auch von „Herdenimmunität“.)
Die derzeitigen Maßnahmen zur Kontaktminimierung (im April 2020) zielen dagegen darauf ab, zu erreichen, dass die sogenannte Reproduktionszahl R (möglichst deutlich) kleiner als 1 ist, das heißt dass jedes Infizierte Individuum im Mittel (möglichst deutlich) weniger als ein weiteres Individuum mit dem Virus infiziert. . Wenn das gelingt, wird die Gesamtzahl der gleichzeitig Infizierten auf Dauer (deutlich) abnehmen. Wenn man die Reprodukionszahl R, ihre zeitliche Entwicklung und die dadurch bedingte Ausbreitung der Infektion durch Kurven veranschaulicht, haben diese Kurven eine andere Bedeutung als die oben diskutierten Kurven und Modelle, weil sich R nicht auf die Gesamtzahl der Infizierten, sondern nur auf die jeweils aktuell Infizierten (ohne die bereits Genesenen und Verstorbenen) bezieht. Selbst in solchen Fällen, bei denen die in den Medien präsentierten Kurven eine mehr oder weniger präzise Bedeutung haben, muss man also genau hinsehen und bei der Interpretation der Kurven vorsichtig sein.
Resumee
Für die Ausbreitung der Corona-Infektion ist also das exponentielle Modell immer nur kurzfristig oder für eine bestimmte Zeitspanne relevant: die Wachstumsraten ändern sich, insbesondere als Folge der getroffenen Maßnahmen, von Tag zu Tag. Global, auf lange Sicht gesehen, wird das Wachstum in ein logistisches Wachstum übergehen. Die getroffenen Maßnahmen zielen jedenfalls darauf ab, dass sich ein exponentielles Wachstum (z.B. in einer „zweiten Welle“) keinesfalls wieder einstellt.
Viele Fragen zum Corona-Virus, u. a. zu seiner Übertragbarkeit, zu seiner Gefährlichkeit, zu seiner Ausbreitungsdynamik, zu seiner Bekämpfung sind heute noch nicht oder nicht vollständig geklärt, und auch anerkannte Experten äußern sich nicht einheitlich über diese Fragen. Insbesondere die Corona-Datenerfassung ist unübersichtlich und uneinheitlich. Über die Gesamtzahl der Infizierten (die „Dunkelziffer“) wird viel spekuliert. Die zugehörige Statistik ist infolgedessen unsicher und oft fragwürdig. Im Hinblick auf die Aufklärung der Öffentlichkeit ist es umso wichtiger, dass das, was man sicher weiß, über die Medien klar und unmissverständlich kommuniziert und veranschaulicht wird, und möglichst nur das.

[…] seinem Blogbeitrag „Exponentielles Wachstum“ (Link) erklärt Ulrich Trottenberg die Bedeutung von Exponentiellem Wachstum im Kontext der Corona […]