Q6 Zwischenspiel - ZBIT-Spielereien

Hier wollen wir mit dem verbesserten ZBIT-Modell aus Q5 ein wenig rumspielen, um mit dem Modell und den Definitionen ein wenig vertrauter zu werden. Um so leichter fällt dann der letzte (kleine) Schritt zum Qubit. Wegen des letzten Abschnitts ist dieser Blog etwas länger geraten. Dafür führt er uns aber zu einer Modell-Darstellung, die schon die für das Qubit-Modell sein wird. Wer keine Lust hat zum Spielen, kann auch einfach nur einen Kaffee trinken und gleich mit dem nächsten Blog weitermachen.

Wir hatten schon festgestellt, dass die inneren Zustände eigentlich beliebig wählbar sind, vorausgesetzt, die Maschinen-Tabellen (Output und Zustandsübergänge) sind konstistent.

1. Alice, Bob, Charly und Debbie

Statt [00] usw. können wir z.B. Namen nehmen:

Alice, Bob, Charly und Debbie statt [00], [10], [01], [11]. Wenn wir die vier dann als Ecken eines Quadrats aufstellen, etwa in der Sporthalle, können wir das Modell als Ballspiel beschreiben:

1. Jede Runde beginnt bei Alice, sie hat den Ball (Operation R)
2. Jeder spielt den Ball entsprechend den Regeln von X und H.
3. Jeder ist dabei frei, welche der Regel sie oder er „werfen“ will
4. Irgendwann pfeift der Referee ab (M)

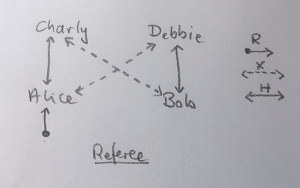Die Grafik illustriert das Set-up. Die Pfeile zeigen, wie X und H gespielt werden dürfen. Da die Personen formal Zustände sind, zeigt die Grafik ein sog. Zustandsüberführungs-Diagramm, ein Wort, das man üben muss.

Wir haben noch nicht gesagt, was D, L und P sein sollen. Da wir die inneren Zustände und Übergänge beim Ballspiel beobachten, könnten wir trivialerweise festlegen: D, wenn der Ball bei Abpfiff bei Alice ist, L, wenn er bei Debbie ist und P, wenn er bei einem der beiden anderen ist. Das ist nicht beonders interessant.

Wie wäre es, wenn bei Abpfiff der Ball in einen Basketball-Korb geworfen werden muss? Das ganze Spiel findet hinter einem Vorhang statt, sodass wir es nicht sehen können. Allein den Wurf auf den Korb können wir sehen. Dabei bedeutet D, dass der Ball niemals versenkt wird (Alice), L, dass er mit Sicherheit reingeht (Debbie), und P, dass er manchmal trifft und manchmal nicht, im Verhältnis 1:1.

Fragen: Können wir herausfinden, wer den Ball zum Korb wirft? Wie wäre es, wenn wir dem Team bzw. dem Referee Spielpläne vorgeben würden (Algorithmen)? Wie könnte ein „autonomes“ Spiel aussehen? D.h. jeder Spieler entscheidet (zufällig) welchen der möglichen Würfe (R, X, H, M) er oder sie macht.

Wer Lust hat, kann Überlegungen oder Antworten als Kommentar einfügen.

Nun gut, lassen wir die vier weiter spielen und wenden uns einer Darstellung zu, mit der wir das ZBIT-Modell simulieren können.

2. Ein ZBIT-Box Simulationsmodell

Wir haben im Beitrag „Etwas ist anders – Hello Qubit World“ die Partitur eines QuBit-Algorithmus gesehen – ohne zu wissen, worum es geht. Solche Partituren können, wenn sie fehlerfrei sind, von Quanten-Computern oder auch von QC-Simulatoren abgearbeitet werden. Es wäre doch interessant, wenn wir die ZBIT-Experimente in diese Form bringen könnten und sie dem Simulator vorlegen könnten.

Da die Experimente mit den ZBIT- und BIT-Modellen schon in Anlehnung an die „Partitur-Form“ beschrieben wurden, sollte es uns tatsächlich leicht fallen.

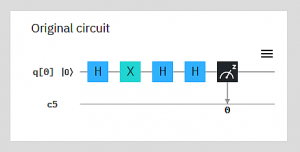
Die Modell-Beschreibung für den QC-Simulator ändert sich kaum: X und H werden vom Simulator „verstanden“, das R gibt es nicht explizit, sondern jede Partitur beginnt mit dem Ausgangszustand.  Der wird im Simulator mit |0> gekennzeichnet statt mit [00], aber die Namen der inneren Zustände sind ja unwesentlich. (Was |0> bedeutet, werden wir später sehen.) Das Anzeige-Symbol („Tacho-Nadel“) steht für die Operation M (Messen).

Anders als bei den bisherigen Modell-Beschreibungen können wir nichts über die inneren Zustände des Simulators wissen. Die Zeile der Zustandsübergänge in den bisherigen Experimenten ist nicht verfügbar – jedenfalls beim QC. Die Messergebnisse des Simulators können ‚0‘ oder ‚1‘ sein, das entspricht dem D und L im ZBIT-Modell. Was wir für P bekommen sehen wir im Experiment.

Wir nehmen das ZBIT-Vorhersage-Experiment aus dem vorausgehenden Blog:

R —— H —– X —– H —- H —– M -> P

und bilden es ab auf den QC-Simulator (hier: IBM Q Experience Circuit Composer).

Mit dem QC-Simulator können wir dieses Experiment einmal durchführen und erhalten:
{‚0‘: 1}. Wir wiederholen und bekommen wieder ein {‚0‘: 1}, dann ein {‚1‘: 1}. Das bedeutet, die ersten drei Experiment-Durchläufe resultierten jeweils in einer  ‚0‘, bzw. einer  ‚1‘. Wir bekommen also D oder L als Output. Wie bei der ZBIT-Box machen wir jetzt Mehrfach-Experimente, z.B. eine Serie von 50 Durchläufen. Das Ergebnis:

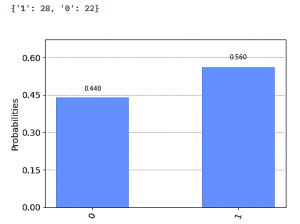also 28 mal L und 22 mal D in unserer ZBIT-Interpretation.

Das sieht schon recht spannend aus. Im Prinzip könnten wir alle bisherigen Experimente mit dem BIT-Modell und dem ZBIT-Modell in dieser Weise simulieren. Damit kommen wir dem Konzept von Qubit-Algorithmen schon sehr nahe.

Und wir gewinnen eine wichtige Erkenntnis: ZBIT (das verbesserte) und BIT sind Teilmodelle des – hier noch unbekannten – Qubit-Modells.

Wer Lust hat, kann nicht nur Fragen und Antworten als Kommentar unten anfügen, sondern auch unter IBM Q Experience sich registrieren und schon mal im Circuit Composer stöbern. Wir schauen uns das in einem späteren Blog noch mal näher an. Eine ähnliche Umgebung bietet auch Google an mit Cirq.

Nun wenden wir uns einer Darstellung zu, mit der wir das ZBIT-Modell  mit einfachen Formeln berechnen können.

3. Ein Modell mit Formeln

Wir wollen nun versuchen, die Zustände so zu definieren, dass man mit ihnen „rechnen“ kann. Statt in den Automaten-Tabellen die Zustandsübergänge nachzusehen, wollen wir sie mit einfachen Formeln berechnen können. Das gleiche für die Outputs.

Eine naheliegende Idee wäre es, die Ziffern in den Zuständen [00] usw. tatsächlich als Zahlen aufzufassen und dazu auch die Output-Ergebnisse in Zahlen umzuwandeln:  D entspricht 0, L entpricht 1, und P dem Wert 1/2. Diese Werte können verstanden werden als Wahrscheinlichkeiten, dass wir Licht sehen, wenn wir die Klappe öffnen. Wir schreiben dafür p(L).

Allerdings hatten wir [00] usw. eigentlich nur als „Label“ für die Zustände eingeführt und  nicht als arithmetische Größen. Daher wäre es ein erstaunlicher Zufall, wenn wir damit ein konsistentes arithmetisches Modell bilden könnten.

Tatsächlich geht das aber, bis zu einem gewissen Punkt. Wer sich davon überzeugen will: es gibt einen Annex zu Q6, in dem das dargestellt wird. Wenn wir allerdings das Modell erweitern wollen, z.B. um Zustände, die p(L) = 1/4 als Output liefern, gibt es Schwierigkeiten.

Wir geben uns daher etwas mehr Freiheit bei der Definition eines rechnerischen Modells, indem wir die Zustände („Labels“), in ein x-y-Koordinatensystem einbetten. (Wir erinnern uns, dass wir mit den zwei-ziffrigen Zuständen in Q5 so etwas wie 2-dimensionale Zustände eingeführt hatten.) Die Zustände werden dann zu Punkten in der x-y-Ebene.

Wir halten die Bezeichnungen [00] bzw. Alice zunächst einmal bei. Sie benennen die Punkt, so wie man Punkte A, B und C eines Dreiecks in der Ebene benennt und mit Koordinaten versieht. Trotzdem können die 0-en und 1-en etwas verwirrend wirken. Die Punkte werden mit ihren Koordinaten in normalen Klammern geschrieben, also z.B. (1,0), die [00] in eckigen Klammern sind die Label der Punkte, ebenso wie die Namen Alice etc.

Das  Einfachste ist, die beiden Zustände [00] und [11] – die ja auch die BIT-Zustände repräsentieren – auf die Koordinaten-Achsen zu platzieren. [00] als Punkt auf der x-Achse bei 1: (x,y) = (0,1). Und [11] entsprechend auf der y-Achse: (x,y) = (1,0). Das Diagramm zeigt wie.

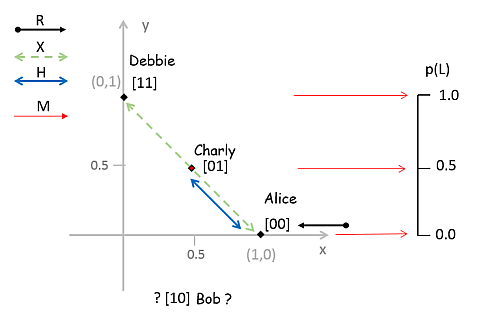
Wo würden wir dann die Zustände [10] und [01] positionieren? Nun, das können wir bereits „ausrechnen“. Schauen wir uns dazu zunächst die passenden Formeln für die Wirkung der Operatoren R, X und H an.

R ist einfach: R(x,y) = (1,0). Das Reset überführt jeden Zustand in den Ausgangszustand, der jetzt die Koordinaten (0,1) hat.

Auch X ist nicht schwer: X(x,y) = (y,x). X als „Switch“ vertauscht die Koordinaten. Das passt schon mal für die beiden vorgegeben Zustände (1,0) <-> (0,1).

Wir haben uns noch nicht um den Output gekümmert. Der Output von (1,0) (i.e. [00]) muss p(L) = 0 sein, der vom (0,1) (i.e. [11]) entspechend p(L) = 1. Es liegt daher nahe, die y-Koordinate als p(L) zu übernehmen. Die x-Koordinate wäre entsprechend als Wahrscheinlichkeit für D zu interpretieren: p(D).

Hieraus folgt direkt und zwingend: p(L) + p(D) = 1.

Damit bekommen wir folgende Bedingungen für die Zustände [10] und [01]:
(1) Sie müssen so positioniert werden, dass die Summe ihrer beiden Koordinaten 1 ergeben.
(2) Der zugehörige Output muß 1/2 ergeben;  die y-Koordinate muss also 1/2 sein.
(3) Wegen der Wirkung von HH, müssen H[00] = [01] und H[11] = [10] unterschiedliche Koordinaten haben.

Man sieht sofort, dass diese Bedingungen unvereinbar sind: [01] kann mit den Koordinaten (1/2,1/2) die Bedingung (1) und (2) erfüllen. Es gibt aber keinen weiteren Punkt, der (1) und (2) erfüllt.

Wir ändern daher die Output-Definition: M (x,y) = p(L) = |y|, d.h. die Wahrscheinlichkeit für L ist der Absolutbetrag von y. Die Bedingungen (1) und (2) werden dann zu
(1′) Die Summe der Beträge der Koordinaten muss 1 sein: |x|+|y| = 1. Und
(2′) Der Betrag der y-Koodinate muss 1/2 sein

Wenn wir dann [10] mit den Koordinaten (1/2,-1/2) versehen, werden alle drei Bedingungen erfüllt. (Siehe Grafik.)

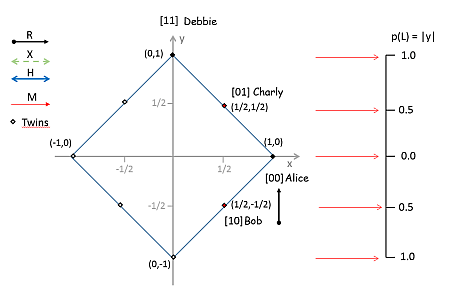
Weiter stellen wir fest, dass aus der Anwendung X und H auf schon bekannte Zustände neue Punkte hervorgehen, die wir ebenfalls als Zustände zulassen müssen.  So muß z.B. mit (1/2,-1/2), den Koordinaten für [10],  auch X(1/2,-1/2) = (-1/2,1/2) = -(1/2,-1/2) ein zulässiger Zustand sein. Wenn H(1/2,-1/2) wieder (0,1) sein soll (doppelte H Anwendung auf [11]), dann muss H(-1/2,1/2) = (0,-1) zulässig sein. Und X(0,-1) = (-1,0) = -(1,0) ebenso. Das Diagramm zeigt die Zustände als Punkte, die Pfeile für die Operatoren sind wegen der Übersichtlichkeit nicht eingezeichnet. Man kann aber, wenn man Lust hat, selbst versuchen, diese Zustandsübergänge einzuzeichnen (gedanklich), soweit es geht.

Das ist zunächst einmal überraschend: Wenn wir die 4 Zustände des ZBIT-Modell durch Punkte im (x,y)-Koordinatensystem darstellen wollen, erweitert sich das Modell zwangsläufig auf 8 Zustände! In unserem ZBIT Ball Game oben, würden dann Alice, Bob, Charly und Debbie jeweils einen Zwilling bekommen, Twin-Alice usw. Eigentümlich – aber niemand zwingt uns, bei einem Modell für die ZBIT-Box mit nur 4 Zuständen auszukommen. Vier ist das Minimum, aber 8 geht auch. Im Diagramm sind die „Twins“ als helle Punkte eingezeichnet. Frage: Welcher Punkt ist Twin von wem?

Damit haben wir für das Koordinaten-basierte Modell:

• Die Zustandsmenge
• Die Wirkung von R und X als Formel
• Die Zustand -> Output Abbildung M mit der Interpretation als p(L), Wahrscheinlichkeit für L als Messergebnis

Was fehlt, ist die Formel für H. Wir hatten festgelegt, dass (1,0) (Label [00]) durch H in (1/2,1/2) überführt werden soll und (0,1) (Label [11]) in (1/2,-1/2). Eine naheliegende Formel für H wäre: H(x,y) = 1/2 (x+y, x-y). Sie liefert für (1,0) und (0,1) genau das, was sie soll. Aber wie sieht es mit (1/2,1/2) und (1/2,-1/2) aus. H auf diese Zustände angewandt müsste ja wieder (1,0) bzw. (0,1) ergeben.

Jedoch: H(1/2,1/2) = 1/2 (1/2+1/2, 1/2-1/2) = 1/2 (1,0). Den gleichen Widerspruch erhalten wir für (1/2,-1/2). Der Faktor 1/2 macht die Inkonsistenz aus. Wenn wir allerdings den Faktor 1/2 in der Definition von H weg lassen, bekommen wir für (1,0) und (0,1) schon gleich falsche Ergebnisse.

Was tun? Vielleicht etwas dazwischen – zwischen 1/2 und 1? Wie es die Mathematiker gerne machen, wenn man sich nicht entscheiden kann, setzt man anstelle von 1/2 eine Variable, sagen wir a, und versucht, dafür einen passenden Wert zu bestimmen. Das ist sehr elegant. Probieren wir also:  H(x,y) = a*(x+y,x-y).

H(1,0) ergibt dann nicht mehr (1/2,1/2) sondern (a,a), was immer a auch ist. Entsprechend H(0,1) = (a,-a). Wenn wir darauf wieder H anwenden, bekommen wir H(a,a) = a*(a+a,a-a) = a*(2a,0) und H(a,-a) = a*(a+(-a),a-(-a)) = a*(0,2a). Andererseits muss H(a,a) = (1,0) sein, also a*2a = 2a² = 1 oder a = 1/sqrt(2). Das klappt auch mit der zweiten Bedingung. Très chic !

Allerdings stehen wir damit wieder am Anfang. Wir müssen die drei Spiegelpunkte oben wieder neu festlegen. Aber dieses Mal lohnt sich die Spielerei; denn wir haben hiermit automatisch die grundlegenden Komponenten für ein Qubit-Modell in Q7 abgeleitet.

• Die 8 Zustände sind (1,0), (0.1), (-1,0), (0-1) und (a,a), (-a,a), (-a,-a), (a,-a) mit a = Wurzel aus 1/2. Alle diese Zustände liegen auf einem Kreis mit Radius 1.0 im x,y-Koordinatensystem. Sie erfüllen die Bedingung x² + y² = 1, die Gleichung des Einheitskreises.
• R und X sind genau wie zuvor definiert, und H als H(x,y) = a*(x+y,x-y).
• Wie ist die Zustand-Output Beziehung? Jetzt ergibt M(x,y) = y² das p(L), die Wahrscheinlichkeit für L bei einer Messung. Und p(D) ist entsprechend x² = 1-y², was ja für alle Zustände auf dem Einheitskreis stimmt.

Das Diagramm zeigt das ZBIT-Modell mit diesen Festlegungen.

Der letzte Abschnitt war sicher keine einfache Spielerei mehr. Aber wir haben es geschafft. Und, wie wir sehen werden, gleichzeitig DAS Werkzeug für Qubit-Algorithmen gefunden.

Frage: Wie würde das ZBIT Ball Game aussehen, wenn wir die vier neuen Spieler ins Feld bringen würden –  nennen wir sie Twin-Alice, Twin-Bob, Twin-Charly und Twin-Debbie? Wer Lust hat usw.

Im nächsten Blog, versprochen, kommen wir aber zum QuBit-Modell – zumindest in einer ersten Form.

Fortsetzung folgt – Stay tuned!