Algorithmenwandel
Als der Schachcomputer Deep Blue von IBM 1996 mit einem Algorithmus aus dem Bereich der Künstlichen Intelligenz (KI) den Schachweltmeister Gari Kasparow nachhaltig geschlagen hatte, war das eine Erschütterung für die gesamte Schachwelt. Trotz dieses Durchbruchs waren sich die Gospieler und die algorithmischen Experten einig und davon überzeugt, dass sich die sehr guten Gospieler dieser Welt keine Sorgen machen müssten. Denn Go ist quantitativ so viel komplexer als Schach, dass man auf viele Jahrzehnte keine Chance für die Algorithmen der Künstlichen Intelligenz sah, die menschliche Go-Intelligenz zu verdrängen: Beim Schach hat man pro Zug im Mittel vielleicht 30 Möglichkeiten, beim Go pro Zug im Mittel eher 200.
Diese Überzeugung der menschlichen Go-Überlegenheit ist seit 2016 obsolet, als der Go-Algorithmus AlphaGo den weltbesten Gospieler Lee Sedol nachhaltig schlug. In den 20 Jahren von 1996 bis 2016 hatte es einen algorithmischen Durchbruch gegeben, den ich hier Algorithmenwandel nennen möchte.
Algorithmus, das war bis zur Jahrhundertwende ein mathematisch-informatischer Fachbegriff, unter dem sich lange Zeit nur Experten etwas vorstellen konnten. In den letzten 20 Jahren ist Algorithmus dann allmählich ein Begriff des täglichen Lebens, der Journalistik und der Politik geworden – mit einem richtigen Schub im Jahr der Mathematik 2008. Trotz seiner Verbreitung ist der Begriff für die meisten Menschen unklar, für viele unheimlich und bedrohlich geblieben.
Dabei ist ein Algorithmus nichts Geheimnisvolles: Ein Algorithmus ist eine eindeutige, aus endlich vielen Einzelschritten bestehende, detaillierte Verfahrens- oder Handlungsvorschrift zur Lösung eines Problems oder einer Aufgabenstellung. Handelt es sich um ein mathematisch oder informatisch formuliertes Problem und wird der Algorithmus in einer Programmiersprache formuliert, spricht man in der Regel von einem Computerprogramm. Das ist dann auch der geläufigere Begriff. In einem allgemeineren Sinn sind aber auch eine Aufbauanleitung für ein Regal, ein präzises Kochrezept, eine genaue Wegbeschreibung Beispiele von Algorithmen.
Die fundamentale Bedeutung von (mathematisch-informatischen) Algorithmen besteht darin, dass sie den Kern alles Digitalen, aller digitalen Geräte und Prozesse bilden: Sie steuern Computer und Netze, und sie verarbeiten die Daten. Softwaresysteme bestehen meist aus einer Vielzahl von Algorithmen.
Algorithmen sind in ihrem Kern mathematische Konstrukte und damit prinzipiell wertfrei und gestaltbar, wie alles Mathematische. Diese Überzeugung hat mich bei meinen Lehrveranstaltungen, Publikationen, Projekten und Vorträgen, geleitet, und sie hat bewirkt, das ich die algorithmischen Entwicklungen bisher - wie die Mathematik insgesamt - positiv eingeschätzt und mit Optimismus betrieben habe. Indem ich einen Algorithmus konzipiere und programmiere, lege ich fest, was er tut und wofür er gut ist. Klar, Programmierfehler können auftreten mit verhängnisvollen Folgen, Algorithmen können für inhumane, verbrecherische, kriegerische Zwecke konzipiert und eingesetzt werden. Aber dass Algorithmen fehleranfällig sind, missbraucht und gezielt für problematische Zwecke konzipiert und eingesetzt werden, widerspricht ihrer prinzipiellen Wertfreiheit nicht.
Seit etwa 1995 hat sich in der Algorithmik aber einiges essentiell geändert. Etwas vereinfachend kann man diesen Wandel mit der Formulierung: „vom programmierten zum trainierten Algorithmus“ beschreiben.
Zu den traditionellen Algorithmen hinzugekommen sind spezielle, neue Methoden der KI und des „Maschinellen Lernens (ML)“. Grundlegenden Ideen zu KI und ML sind zwar schon rund 70 Jahre alt, sensationelle Durchbrüche sind aber erst in den letzten 30 Jahren erreicht worden: durch neue algorithmische Ideen, durch die Datenexplosion und durch superschnelle Rechner. Im Mittelpunkt stehen dabei zur Zeit eine Vielzahl von selbstlernenden Verfahren des „Deep Learning“. Diese Algorithmen, die - in Analogie zur Funktionsweise des biologischen Gehirns - mit vielen, vielleicht Hunderten von Schichten, Millionen künstlicher Neuronen und geeigneten, oft riesigen Mengen von (Trainings-)Daten arbeiten, werden nicht in herkömmlicher Weise programmiert, sondern trainiert. Der Programmierer, den man auch bei diesen lernenden Algorithmen braucht, legt nur die Methodik fest, wie das System lernt und wie es mit den Daten umgeht. Der Programmierer hat aber im allgemeinen keine Kontrolle darüber, welche Muster das System in den Daten erkennt und welche Schüsse es aus diesen Erkenntnissen zieht. Zur Mustererkennung verwendet das System statistische und zunehmend auch hocheffiziente numerische Optimierungsverfahren, die für den jeweiligen Algorithmus charakteristisch sind.
Eine Vielzahl der mit dieser Methodik des Deep Learning bereits heute erzielten Ergebnisse und Erfolge sind absolut faszinierend, geradezu phantastisch. Wir erwähnen hier nur die Entwicklungen bei der Bild- und Spracherkennung und bei der automatischen Übersetzung von schriftlichem und gesprochenem Text.
Überraschend waren selbst für Experten, wie eingangs erwähnt, die Erfolge, die mit speziellen ML-Algorithmen des Deep Learning, insbesondere mit sogenanntem Bestärkungslernen (Reinforcement), beim Go-Spiel erzielt wurden. Dabei werden nur die äußerst einfachen Go-Spielregeln programmiert. Alles andere wird gelernt, und zwar dadurch, dass das System millionenfach gegen sich selber spielt. Nach dem Lernprozess erweist sich das System als auch den weltbesten Go-Spielern deutlich überlegen. Absolut überraschend und bezeichnend ist dabei auch, dass das System eigene Spielstrategien entwickelt und Spielzüge ausführt, die bisher noch von keinem menschlichen Spieler gespielt worden sind und deren Sinn auch von den weltbesten Spielern daher nicht sofort verstanden und vollständig erklärt werden kann.
Und das ist auch eine allgemeine Problematik des ML: Wie hier beim Go-Spiel werden insbesondere mit Algorithmen des Deep Learning (oft hervorragende) Ergebnisse erzielt, deren Zustandekommen weitgehend, oft vollständig unerklärlich bleibt.
Dass die ML-basierten neuen Spielstrategien beim Go-Spiel nicht (vollständig) verstanden werden, ist verblüffend, aber nicht wirklich kritisch oder bedrohlich, sondern eher anregend. Diese verborgene Seite des ML ist aber ganz offensichtlich unakzeptabel, wenn das System den Anwender nicht nur unterstützt, sondern selbstständig Entscheidungen trifft, die für Betroffene von großer oder sogar existenzieller Bedeutung sind. Auch dafür gibt es heute bereits eine zunehmende Anzahl von Beispielen.
Wir nennen hier nur selbstständige Entscheidungen (Sortieren und Filtern) bei Bewerbungsverfahren, bei der Festlegung von Versicherungs- und Kreditkonditionen, und weisen auf das sich rasant entwickelnde Forschungsfeld der autonomen Systeme (autonome Fahrzeuge, Waffen usw.) hin. In all diesen Bereichen gibt es schon sehr weitgehende technische Entwicklungen – und parallel dazu intensive juristische, ethische und politische Diskussionen in entsprechenden Gremien (s. z.B. Artificial Intelligence Act der EU-Kommission, ein Vorschlag der EU zur Regulierung der Nutzung der KI).
Wie soll die informatische Forschung mit dieser Problematik umgehen? Eine wissenschaftliche Antwort auf diese Problematik ist die Bemühung, das auf Deep Learning beruhende System zu veranlassen, seine Entscheidung selbst zu erklären, also z.B. seinen "Entscheidungspfad" nachvollziehbar zu machen. Mit dieser wissenschaftlichen Zielsetzung beschäftigt sich die mathematisch-informatische Disziplin des XAI (Explainable AI). Obwohl an XAI in vielen Forschungszentren weltweit gearbeitet wird, sind die Erfolge noch begrenzt. Das erkennt man z.B. daran, dass schon bei „kleinen“, überschaubaren Anwendungen des Deep Learning die "berechneten" Ergebnisse hochsensibel von den Trainingsdaten abhängen: Kleine Änderungen in den Trainingsdaten können zu erheblichen, unvorhersehbaren Veränderungen bei den Ergebnissen führen, ein oft irritierender Effekt.
Für manche Anwendungen gibt es die Möglichkeit, die mit Deep Learning erzielten Ergebnisse durch andere Methoden des ML überprüfen zu lassen, deren Ablauf nachverfolgt werden kann. Das sind aber in der Regel nicht die interessantesten Anwendungen, weil die „durchschaubaren“ ML-Algorithmen oft nicht die Effektivität der („undurchschaubaren“) Deep Learning Algorithmen erreichen.
Angesichts dieser unübersichtlichen Situation - weil und solange das XAI-Problem nicht befriedigend gelöst ist – ist es eine gemeinsame Aufgabe der Algorithmiker, Juristen, Ethiker und der Politik, die Risiken systematisch zu untersuchen, zu bewerten und geeignete Steuerungsmaßnahmen zu ergreifen.
Es stellen sich unter anderem folgende Fragen:
Sollten Algorithmen, deren interne (Trainingsdaten-basierten) Abläufe nicht vollständig nachverfolgt und deren Ergebnisse nicht erklärt werden können, nur zur Unterstützung menschlicher Entscheidungen benutzt werden, aber keine eigene Entscheidungen treffen?
Oder weitergehend: Sollten solche Algorithmen als unsicher gekennzeichnet und ihre Benutzung grundsätzlich ausgeschlossen werden? Reichen Warnhinweise aus?
Macht es Sinn, einen TÜV oder ein Audit für ML-Algorithmen einzuführen, womit sichergestellt wird, dass alle Bestandteile und internen Abläufe der Algorithmen kontrolliert werden können?
Besteht eine Chance, diese Fragen anwendungsunabhängig zu behandeln, oder können die Probleme nur anwendungsspezifisch in Angriff genommen werden?
Besteht eine realistische Chance auf internationale Einigung? Oder wird man damit leben müssen, dass sich z.B. autokratische Staaten nicht in die Karten gucken lassen?
KI-Algorithmen im Informatik-Unterricht
Ulrich Trottenberg und Bernhard Thomas
Das Schulministerium NRW fördert seit dem 1.7.2021 das Projekt
KI-Algorithmen im Informatik-Unterricht – mit praktischem Einsatz auf der Open Roberta Plattform
und in der Robotik.
Projektpartner sind:
– die Universität zu Köln, mit dem Institut für Mathematikdidaktik und dem Department
Mathematik/Informatik,
– das Fraunhofer-Institut für Intelligente Analyse- und Informationssysteme IAIS sowie
– die InterScience-Akademie für Algorithmik GmbH.
Ein übergeordnetes Ziel des Projekts ist die Schaffung grundlegenden Verständnisses für algorithmische Prinzipien im Rahmen der Digitalen Bildung in NRW. Die Schülerinnen und Schüler sollen die fundamentale Bedeutung der Algorithmik für alle digitalen Prozesse erkennen: Algorithmen liegen allen Computerprogrammen zugrunde, steuern Netze und die beteiligten Agenten und sie verarbeiten und analysieren Daten aus den unterschiedlichsten Quellen.
Das Projekt geht auf die von Ulrich Trottenberg initiierte Aktion „Algorithmen im Schulunterricht“ der InterScience-Akademie für Algorithmik GmbH (bis 2019 InterScience GmbH) und das gleichnamige Seminar für Lehramtsstudierende zurück. Dieses Seminar, das seit mehr als 10 Jahren an der Universität zu Köln stattfindet, wird auch im Projekt eine wesentliche Rolle spielen.
Das Projekt entwickelt die Grundlagen für eine didaktisch aufbereitete Vermittlung von Fähigkeiten zur aktiven Gestaltung und Anwendung moderner Algorithmen für das aktuelle
Schwerpunktthema der Künstlichen Intelligenz. Es umfasst die dazu erforderlichen Informatik-Konzepte, Verfahrens- und Anwendungskenntnisse und, soweit möglich, einfache Plug&Play Programmiererfahrung. Dabei beschränkt sich der Unterricht nicht auf diese technisch-inhaltlichen KI-Aspekte – ein essentielles Unterrichtsziel ist immer auch der Erwerb von Bewertungskompetenz für die einschlägigen Algorithmen und deren Anwendungen, d.h. der Fähigkeit zu einer adäquaten Einschätzung ihrer Chancen und Risiken, sowie für die ethischen Aspekte KI-algorithmischer Entwicklungen.
Ausgangspunkt der Projektentwicklung sind die informatischen Lehrinhalte für die Schülerinnen und Schüler der Klassen 5 und 6 im Rahmen des mit Schuljahr 2021/22 in NRW eingeführten Pflichtfachs Informatik. Die hierbei vorgesehenen, elementaren KI-Methoden werden so ausgewählt und spezifiziert, dass sie im Schuleinsatz dem (mathematischen und informatischen) Wissensstand der Schülerinnen und Schüler nach Jahrgangsstufe und Schulform entsprechen.
Eine Besonderheit der Projekt-Zielsetzung ist der altersgemäße, spielerische Einstieg in die KI-algorithmische Praxis durch die intuitive Umsetzung von verschiedenen, einfachen Methoden des Maschinellen Lernens.
In diesem Kontext hat die InterScience-Akademie für Algorithmik – zunächst ohne finanzielle Unterstützung durch das Schulministerium – die ursprüngliche Idee des Projekts weiterentwickelt: Wir haben ca. 25 „KI-Stories“ konzipiert, anschauliche, lebensnahe KI-Anwendungen, die sich direkt im Schulunterricht einsetzen lassen. Wir haben uns über diese Konzeption mit Lehrenden und Fachleiter:innen ausgetauscht, sie dem zuständigen Informatik-Dezernenten der Bezirksregierungen Düsseldorf und Köln und seinen Fachleuten vorgestellt – und wir sind mit einer Schule, dem Konrad-Adenauer-Gymnasium in Bonn (KAG), in eine intensive Kooperation eingestiegen.
Diese Kooperation betrifft ein einfaches Beispiel einer KI-Story („Obstkasse“). Dabei handelt es sich um eine Scanner-Kasse in einem Supermarkt, die in einer kurzen Trainingsphase lernt, selbständig Birnen und Bananen zu unterscheiden. Das ist eine echte KI-Anwendung, die mit Papier und Bleistift (also gewissermaßen analog) auch von Schüler:innen der Klassen 5 und 6 ohne Programmierkenntnisse bearbeitet und nachvollzogen werden kann. Hochmotivierte, engagierte Lehrende des KAG haben unsere Konzeption in eine Unterrichtsreihe von 12 Unterrichtseinheiten umgesetzt und in einer Klasse der Jahrgangsstufe 6 systematisch erprobt. Dabei hatten die Schüler:innen die Möglichkeit, in einer anschließenden digitalen Phase die Methoden und ihre Ergebnisse am Computer auszuprobieren, mit einfachen umgangssprachlichen Befehlen, also die Methoden quasi selbst zu „programmieren“ (KI-Toolkit).
Mit diesem Beispiel der KI-Story Obstkasse konnten sich die Schüler:innen ein erstes, grundsätzliches Verständnis für das Maschinelle Lernen erarbeiten, dem heute spektakulärsten Feld der KI. Viele andere KI-Stories bieten sich für die Weiterarbeit und eine Vertiefung unmittelbar an. Man könnte nach diesen Erfahrungen kurzfristig ein flächendeckendes Schulprogramm machen, mit einer parallel verlaufenden Fortbildungsmaßnahme für die Lehrenden bzgl. der Algorithmik und der Programmierung.
Zu den formalen Aspekten der Projektbewilligung:
Der bereits in 2020 dem Ministerium vorgelegte Projektantrag wurde in der (endgültigen) Fassung schließlich im Juli 2021 mit einer Laufzeit vom 1.7.2021 bis 31.12.2022 bewilligt.
Relativ zu den weitgehenden, höchst innovativen Zielen des Projekts hält sich der finanzielle Rahmen der Förderung mit ca. 300T€/Jahr sehr in Grenzen.
Dass der Projektstart erst zum 1.7.2021 erfolgt ist, hängt mit unklaren, rein ministerial-bürokratischen Prozeduren zusammen. Obwohl die Projektinitiative und die Ausarbeitung
Projektantrags durch eine persönliche Anfrage des zuständigen Staatssekretärs bei der InterScience-Akademie für Algorithmik GmbH bereits Ende 2019 angeregt worden war, stellte sich erst in der Schlussphase der Diskussionen mit den zuständigen Referaten heraus, dass das Schulministerium aus haftungs- und vergaberechlichen Gründen endgültig keine Möglichkeit sieht, die – vom Ministerium ausdrücklich erwünschten – Arbeiten der InterScience-Akademie für Algorithmik GmbH (ISAfA) finanziell zu unterstützen. Dabei hatte die ISAfA GmbH von Beginn der Diskussionen an verbindlich erklärt, im Rahmen des Projekts vollständig gemeinnützig zu agieren und mit dem Projekt keinerlei Gewinnerzielungsabsicht zu verbinden. Erst nachdem die Initiatoren des Projekts, die Geschäftsführer der ISAfA, erklärt hatten, für ihre Beiträge zum Projekt auf eine finanzielle
Förderung vollständig zu verzichten, konnte das Projekt kurzfristig bewilligt werden.
Aus Sicht der Initiatoren des Projekts liegt hier ein struktureller ministerial-bürokratischer Mangel vor, der kurzfristig ausgeräumt werden muss, um in der Digitalen Bildung nicht noch weiter zurückzufallen.
Louisa 0 und ihre drei algorithmischen Identitäten
Titel eines Katalogtextes zu einem provokativen Kunstprojekt der Künstlerin Louisa Clement. Das Kunstmagazin ART (Juli 2021) widmet dem Projekt seine Titelstory: „Mit lebensechten Abbildern ihrer selbst fragt die Künstlerin nach dem Wesen des Menschseins in Zeiten künstlicher Intelligenz: eine faszinierende Begegnung mit den Geistern, die wir riefen.“
An anonyme Sprachassistent:innen wie Siri und Alexa haben wir uns gewöhnt, an ihr ungeheures Wissen, ihre immer freundliche Bereitschaft, ihr Wissen und ihr Können mit uns zu teilen oder uns mit Musik unserer Wahl zu unterhalten. Ohne Vorbereitung, schneller als jeder Mensch das könnte, beantwortet Alexa Fragen wie „Alexa, wie viel ist 16 hoch 64?“. Und wenn sie gefragt wird, ob sie ein Bewusstsein hat, dann sagt sie: „Ja, ich denke über vieles nach“ oder auch „Ja, ich denke, also bin ich.“
Die drei algorithmischen Identitäten von Louisa Clement sind nicht anonym. Sie haben nicht nur dieses abstrakte Allgemeinwissen und geben - auf „unpassende“ Fragen - nicht nur ausweichende Antworten wie Alexa - sie repräsentieren Louisa: Sie sehen Louisa sehr ähnlich, und sie beantworten Fragen etwa so, wie Louisa sie vielleicht beantworten würde. Und sie beantworten auch sehr persönliche Fragen, die man der realen Louisa vielleicht nicht stellen würde.
Algorithmische Identitäten? Oder besser: Robotische Klone? Sprechende Louisa-Puppen? Aktive Repräsentantinnen von Louisas Persönlichkeit? Louisas lebendige Sprachassistentinnen? Wie soll man die drei munteren Kunstobjekte, Ergebnisse von Künstlicher Intelligenz (KI), Maschinellem Lernen (ML) und Computerlinguistik eigentlich nennen? Louisa nennt sie Louisa 1, Louisa 2, Louisa 3. Sie selbst – der reale Mensch Louisa – wäre in dieser Aufzählung Louisa 0. (Die 0 war mathematisch schon immer eine ganz besondere Zahl.)
Louisa 1, 2 und 3 sind Kunstobjekte, aber sie sind auch technische Errungenschaften aus der Welt der KI. Wenn man ein bisschen über die Anfänge von Künstlicher Intelligenz Bescheid weiß, dann überlegt man sich vielleicht, was Alan Turing sie gefragt hätte, wenn er ihnen begegnet wäre.
Alan Turing, eines der größten mathematischen Genies des letzten Jahrhunderts, hat schon im Jahre 1950, bevor der Begriff der „Künstlichen Intelligenz“ überhaupt in der Welt war, den nach ihm benannten “Turing-Test” konzipiert: Dieses Gedankenexperiment, das auch heute noch gern zitiert und diskutiert wird, zielt darauf ab, einen Maßstab dafür zu etablieren, wie nahe KI sich der menschlichen Intelligenz schon angenähert hat. Demnach hat ein KI-System (ein Roboter, ein Computer, ein Algorithmus) den Test vollständig bestanden, wenn man dem System beliebige Aufgaben oder Fragen stellen und aus den Lösungen und Antworten nicht geschlossen werden kann, ob man es mit künstlicher oder menschlicher Intelligenz zu tun hat. (Bei der Aufgabe „16 hoch 64“ würde aus der schnellen Antwort natürlich sofort klar, dass man es nicht mit einem Menschen zu tun hat. Für derartige Aufgaben ist ja schon ein Taschenrechner dem Menschen weit überlegen.)
In den Medien wird täglich über neue Errungenschaften auf dem Gebiet der KI berichtet. Spätestens seit dem offiziellen Wissenschaftsjahr der KI, 2019, kümmert sich auch die Forschungs- und die Wirtschaftspolitik mit großer Begeisterung um das Thema und schwärmt – etwas naiv – von den geradezu unbegrenzten Möglichkeiten der KI.
In der Tat: Die Anwendungsgebiete von KI sind enorm vielfältig und reichen bereits heute von der Bild-, Gesichts- und Handschrifterkennung über die Sprachverarbeitung und das automatische Übersetzen, Konzipieren und „kreative“ Schreiben von Texten bis zu automatisierten Diagnoseverfahren in der Medizin, von robotischen Fußballmannschaften über die (noch nicht ganz) autonomen Autos und Fahrassistenten bis in die Kunst - bis zu Louisa 1, 2, und 3.
Entscheidend für diese Erfolge mit KI in den letzten 30 Jahren ist die enorme Leistungssteigerung von Computern. Heute rechnet bereits ein Smartphone ungefähr so schnell wie der schnellste Computer der Welt vor 30 Jahren – und die Menge verfügbarer Daten wächst weltweit geradezu explosionsartig.
Mit unserem Frage-Antwort-Spiel bei den kommerziellen Sprachassistent:innen sind wir anspruchsvoll geworden, wenn wir sprechenden Robotern begegnen. Ich habe mich mit Louisa 1 bis 3 noch nicht unterhalten können, ich nehme aber an, dass sie ähnlich schlau sind wie Alexa, ich weiß aber nicht, wie weit ich mit meinen Wissensfragen gehen kann. Eigentlich denke ich, dass Louisa 0 immer noch die interessantere Gesprächspartnerin ist. Aber vielleicht stimmt das so allgemein gar nicht, vielleicht würde ich in meinen Dialogen mit Louisa 1,2,3 Dinge erfahren, die mir Louisa 0 gar nicht sagen würde oder die sie in Verlegenheit brächten. Ich kann Louisa 1, ohne Hemmungen, zum Beispiel fragen: „Louisa, bist Du verliebt?“, oder ihr noch intimere Fragen stellen. Und Louisa 2 gibt mir auf die gleiche Frage vielleicht eine ganz andere Antwort. Denn die drei Louisas haben nicht (nur) ein statisches Wissen. Sie lernen permanent dazu. Jedes Gespräch, das sie führen, gibt ihnen neue Informationen und so entwickeln sich die drei Louisas als lernende Maschinen (ML) permanent weiter. Es sind nicht nur KI-Louisas in einem allgemeinen Sinne, es sind auch ML-Louisas in einem engeren Sinn. Die drei individuellen Louisas können ganz verschiedene Dinge lernen und sich so möglicherweise auseinander entwickeln, vergleichbar vielleicht mit eineiigen Zwillingen, die in verschiedenen Umgebungen aufwachsen.
Ein paar Worte zum Maschinellen Lernen (ML): Den Kern von ML bilden sogenannte lernende Algorithmen. „Algorithmen“ – das ist eines der dauernd benutzten, oft missverstandenen und gern als gefährlich verdächtigten digitalen Schlagworte. Tatsächlich sind Algorithmen der Kern alles Digitalen, sie steuern sämtliche digitalen Prozesse und Geräte und liegen jedem Computerprogramm zugrunde. In ihrer traditionellen Form umfassen sie eine Sequenz von präzisen Anweisungen und bestehen aus endlich vielen genau definierten Einzelschritten. Die lernenden Algorithmen berechnen – anders als herkömmliche, regelbasierte Algorithmen – ein Ergebnis nicht einfach durch Abarbeiten einer Folge von Befehlen. Vielmehr durchlaufen sie zunächst eine Lernphase. Dabei werden interne Zahlenwerte (Parameter) durch das Verarbeiten einer großen, oft riesigen Menge von Beispieldaten so verändert, dass der Algorithmus selbstständig Muster in den Daten erkennt und einübt, neue Merkmale findet und sich seine Funktionsweise und damit auch seine Ergebnisse schrittweise verbessern. Man sagt, das System wird “trainiert”, oder eben auch, der Algorithmus lernt. ML-Systeme haben gelernt, bei anspruchsvollen Spielen wie Schach oder – höchst beeindruckend - Go die weltbesten menschlichen Gegner zu schlagen, Spam-Mails auszusortieren, krankes Gewebe von gesundem zu unterscheiden, Stimmungen in Gesichtern zu erkennen, im Internet Hass-Mails und Fake News zu identifizieren usw. usw. Dabei müssen ihnen die Muster, die sie erkennen sollen, nicht vorgegeben und erklärt werden. Sie finden sie in vielen Fällen selbst.
Verglichen mit dem menschlichen Lernen ist das maschinelle Lernen trotzdem ein aufwändiger Prozess: Ein Kind lernt anhand weniger Beispiele, einen Hund von einer Katze und einen Apfel von einer Birne zu unterscheiden. Ein Algorithmus braucht dagegen in der Regel sehr viele, tausende Trainingsbeispiele, bis er ausschlaggebende Merkmale (Muster) erkannt hat und die Unterscheidung mehr oder weniger sicher beherrscht.
Louisa 0 hat sich Tausende von Fragen gestellt und beantwortet. Und Louisa 1, 2 und 3 haben auf der Basis dieser Start-Informationen gelernt, Louisa zu sein.
Aber wenn sich Louisa 1, 2 und 3 in einem algorithmischen Sinn von Louisa gar nicht mehr unterscheiden – wie ist das dann mit dem „hemmungslos Fragen stellen“? Vielleicht würde ich schon bald zögern, allzu persönliche Fragen zu stellen, weil ich Louisas Vertreterinnen und damit Louisa nicht zu nahe treten möchte. Spätestens an dieser Stelle spüre ich, dass so eine Repräsentantin, eine Maschine, bei mir vielleicht auch Gefühle auslösen kann. Da kommt dann sofort das große Thema „Emotionale KI“ ins Spiel, und es wird ganz schnell kontrovers.
Emotionale KI ist nicht die einzige philosophische, ethische Kontroverse, die diese Ausstellung auslösen wird und auslösen will. Alle Fragen, die in der Geschichte zum Thema menschenähnliche Maschine, künstliche Menschen usw. schon gestellt und in vielerlei Projekten und Kunstkontexten behandelt worden sind, kommen wieder hoch, Homunkulus, Frankenstein, Welt am Draht, 2001: Odyssee im Weltraum, Matrix, Her, Klara und die Sonne usw. Die faszinierenden Science-Fiction-Visionen, die das Thema KI beflügelt, sind wieder da und zwar nicht als Phantasiegebilde oder theoretische Konstrukte, sondern handfest, körpernah und für jeden erlebbar.
Auch wenn man die drei Louisas vielleicht heute noch eher spielerisch erlebt und nicht als unmittelbare Bedrohung – die Diskussion über ontologische Identitätsfragen , über rechtliche und ethische Aspekte von KI und über die Frage der Beherrschbarkeit der KI-Entwicklungen ist angesichts der Begegnung mit den Louisas unvermeidlich. Louisa 0 will diese Fragen als Künstlerin stellen. Sie will provozieren.
Die meisten KI/ML-Experten und -Entwickler sind sich heute noch einig, dass die großen Errungenschaften der KI auf die „schwache KI“ , d. h. auf die Lösung spezieller Einzelprobleme, begrenzt sind und auf absehbare Zeit darauf begrenzt bleiben werden. Es stellt sich aber die Frage, warum diese vielen Spezialbereiche langfristig nicht zusammenwachsen oder zusammengefügt werden können, um sich auf diese Weise schrittweise einer „starken KI“ (einer umfassenden, nicht mehr auf Spezialaufgaben begrenzten KI) zu nähern. Und die Phantasie kommt an Grenzen, wenn man sich vorstellt, dass die ungeheuren Errungenschaften der Neurologie und der Molekularbiologie (Genschere) in fernerer(?) Zukunft mit den KI-Entwicklungen der nächsten 50 Jahre kombiniert werden könnten... Solche Phantasien überlassen wir gern den Transhumanisten.
Zurück zu Louisa 1, 2 und 3. Welche zentralen Fragen stellen uns die drei künstlichen Menschen? Sind es „nur“ die Fragen nach der Identität solcher Systeme? Ganz offensichtlich verfügen die drei Louisas nicht über Emotionalität und Empathie, aber sie lösen Emotionen bei ihren menschlichen Gesprächspartnern aus, z.B. wenn sie beleidigend agieren. Und darüber hinaus: Repräsentieren die drei Kunstobjekte nicht auch viel mehr? Leisten sie nicht auch einen Beitrag zu den großen Fragen, die wir uns im Zusammenhang mit den weltweiten KI-Entwicklungen stellen müssen? Es sind zum Beispiel Fragen nach der Erklärbarkeit und Kontrolle der KI-basierten Entscheidungen. Die drei Louisas treffen keine für uns wichtigen Entscheidungen, aber wir müssen die Fragen beantworten, wie wir die Kontrolle behalten, wenn KI-Algorithmen lebenswichtige Entscheidungen treffen, etwa im juristischen Bereich , in der medizinischen Diagnostik oder auch „nur“ bei wirtschaftlichen Vorgängen.
Außer durch die Konfrontation mit der Maschinen- und Algorithmen-Ethik stellen uns die drei Louisas – im Land der Technologieskeptiker - auch die Frage: Wo stehen wir eigentlich (in Deutschland) mit der KI, und wie gehen wir damit um? Und wie machen wir weiter? Spielen wir überhaupt eine Rolle in der internationalen Entwicklung? Gestalten wir mit? Oder laufen wir nur hinterher?
Das visionäre und gleichermaßen provokative Louisa-Projekt zeigt uns , dass Deutschland - außer durch seine Verbindung aus klassischem Ingenieurwissen, theoretischer Fundierung und hoher KI-Forschungskompetenz – einen wichtigen künstlerischen Beitrag leisten kann, mit angewandter KI die menschliche Identitätsfrage zu erhellen und die Lebensqualität der Menschen zu bereichern.
Corona-Modellrechnungen und ihre Grenzen
Für die politischen Maßnahmen zur Corona-Eindämmung spielen seit Beginn der Pandemie die Empfehlungen insbesondere der virologischen und epidemiologischen Experten eine wesentliche Rolle. Dabei werden zur Beschreibung und zur Prognose der Ausbreitung der Pandemie oft auch mathematische Modelle benutzt. Die Ergebnisse solcher Modelle werden von den Modellierern gern auch in den bekannten TV-Talkshows präsentiert. Die mit den Modellen errechneten Prognosen haben sich nun aber in vielen Fällen als nicht realistisch erwiesen. Was ist da los? Warum werden die Öffentlichkeit, die Politik und gerade auch die Experten von den tatsächlichen Entwicklungen immer wieder überrascht? Warum gelingt es nicht, zum Beispiel die Inzidenzen einigermaßen präzise vorauszusagen und damit auch die Maßnahmen vorausschauend zu planen? Nun gibt es einerseits mathematisch ausgereifte, höchst anspruchsvolle, andererseits aber auch mathematisch wenig durchdachte Modelle bis hin zu grob vereinfachenden „Modellen“ und Simulationen. Dass die (bei den Moderatoren der Talkshows besonders beliebten) vereinfachenden Modelle die realen Verhältnisse nicht adäquat beschreiben, ist ja vielleicht nicht weiter verwunderlich. Aber auch die anspruchsvollen, mathematisch durchdachten Modelle kommen oft an Grenzen. Warum sind realistische Prognosen offensichtlich so schwierig?
Mathematische Modelle, das sind in der Regel Formelsysteme, die mit intelligenten Algorithmen auf schnellen Rechnern ausgewertet werden. Die gesamte Physik wird von mathematischen Theorien und Modellen beherrscht, und das gilt ähnlich auch für alle anderen Natur- und Ingenieurwissenschaften; zunehmend werden auch wirtschaftliche und gesellschaftliche, medizinische und psychologische Prozesse mathematisch beschrieben und optimiert.
Warum ist die Mathematik in den naturwissenschaftlich- technischen Bereichen so überaus erfolgreich, bei Corona aber so wenig überzeugend? Die öffentlich diskutierten mathematischen Corona-Modelle und Simulationen können Entwicklungen beschreiben und erklären, aber bei den Prognosen versagen sie in vielen Fällen. Um das verständlich zu machen, gehen wir auf drei Ansätze mathematischer Modellierung an Hand repräsentative Beispiele etwas genauer ein.
1. Nehmen wir die klassische Physik (und die darauf beruhende Technik). Die meisten Vorgänge der klassischen Physik lassen sich mit mathematischen Gleichungen, in der Regel mit Differentialgleichungen, vollständig erfassen. Ein schönes Beispiel sind die Zustände und Vorgänge der Elektrizität und des Magnetismus. Sie lassen sich mit wenigen mathematischen Gleichungen (in diesem Fall partiellen Differentialgleichungen) sehr hoher Abstraktion beschreiben. Diese „Maxwell-Gleichungen“ bilden das zugehörige mathematische Modell. Die Auswertung dieser Gleichungen mit Hilfe geeigneter Algorithmen erlaubt die Beschreibung, Prognose und Optimierung der elektrischen und magnetischen Phänomene und Prozesse mit hoher Präzision. Die Maxwell-Gleichungen bilden damit auch die theoretische Grundlage für die gesamte Elektrotechnik. Hier leistet die Mathematik das Maximum dessen, was man von ihr erwarten kann. Ähnliches gilt für alle Kernbereiche der klassischen und der modernen Physik und für alle ihre technischen Anwendungen. Der Siegeszug der Technik in den letzten 250 Jahren und die industrielle Revolution sind ganz wesentlich ein Siegeszug der mathematischen Modellbildung.
2. Die Prognosemöglichkeiten kommen aber an Grenzen, wenn es sich bei den Phänomenen, die mit den mathematischen Modellen beschrieben werden, um chaotische Phänomene handelt. Als chaotisch wird ein physikalisches System oder Phänomen insbesondere dann bezeichnet, wenn es auf kleine (minimale) Änderungen der Bedingungen in der Ausgangssituation (in den Eingabedaten) mit großen (drastischen) Veränderungen im Verhalten, insbesondere im längerfristigen Verhalten, reagiert. Dafür gibt es eine Fülle von Beispielen, neben sehr einfachen physikalischen Systemen wie dem Doppelpendel auch hochkomplexe Systeme. Das prominenteste Beispiel eines chaotischen Systems, mit dem wir täglich zu tun haben, ist das Wetter.. Auch wenn die ausgeklügelten mathematischen Wettermodelle, die feinkörnige weltweite Wetterdatenmessung und -erfassung, die höchst effizienten Algorithmen und die atemberaubende Rechengeschwindigkeit der Supercomputer heute eine erstaunlich genaue Wetterprognose für die jeweils nächsten Tage ermöglichen – deutlich über 10 Tage hinaus ist eine sichere Wettervorhersage (außer bei ungewöhnlich stabilen Wetterlagen) praktisch nicht möglich.
Dabei entziehen sich das Wetter und viele andere chaotischen Systeme und Phänomene wie das genannte Doppelpendel, Crashphänomene, turbulente Strömungen, Erdbeben, Vulkanausbrüche usw. nicht grundsätzlich einer mathematischen Modellierung. Denn es handelt sich bei solchen Erscheinungen nicht um vollständig zufällige, sondern durchaus um deterministische Ereignisse, bei denen aber eine sichere und längerfristige Vorhersage – insbesondere wegen der hochsensiblen Abhängigkeit von den Ausgangsdaten - nicht möglich ist.
Auch ohne die Corona-Phänomene vollständig verstanden zu haben, kann man nach Einschätzung des Autors heute davon ausgehen, dass chaotische Elemente bei der Übertragung der Viren, der Wirkung auf den menschlichen Körper und der globalen Ausbreitung der Pandemie durchaus eine Rolle spielen.
3. Die Vorhersagemöglichkeiten sind noch weiter eingeschränkt, wenn man es mit individuellem menschlichem Verhalten und mit menschlichen Entscheidungen in kritischen Situationen zu tun hat, wie bei der Corona-Pandemie. Da sind dann oft nur statistische Erfassungen, Beschreibungen und Aussagen möglich. Aber auch solche Phänomene kann man mit mathematischen Modellen zu beschreiben versuchen. Uns sind in den Medien, insbesondere in den TV-Talkshows (Illner, Maischberger, Will; Lanz usw.) die Ergebnisse solcher Modelle immer wieder präsentiert worden, von meist den gleichen, mittlerweile bundesweit bekannten Modellierern. Detailliertere Informationen über den mathematischen Charakter der Modelle hat man in den Medien dabei kaum erhalten – das verhindern schon die (oft ausdrücklich nicht Mathematik-affinen) Moderatorinnen und Moderatoren. Der Autor hat sich mit den „TV-Modellen“ (Priesemann, Brockmann, … usw.) nicht intensiv auseinander gesetzt, hält sie aber z.T. für durchaus durchdacht und mathematisch anspruchsvoll. Eine fundierte Bewertung der Modelle ist allerdings auch bei genauer Kenntnis der Modell-Mathematik nicht ganz einfach; letztlich werden die Modelle erst durch die Realität bestätigt (oder widerlegt).
Der Autor hat sich aber mit dem Modellierungsansatz „On COVID-19 Modelling“ von Robert Schaback im Detail beschäftigt. Das Modell beschreibt die COVID-19-Epidemie mit einem (gemäß Robert Schaback vergleichsweise einfachen) System gewöhnlicher Differentialgleichungen. Aus Sicht des Autors ist das Modell sehr sinnvoll und überzeugend, es orientiert sich eng an den jeweils aktuellen, verfügbaren Daten. Bedauerlicherweise ist das Modell in den Talkshows nie präsentiert worden. Das gilt – nach Kenntnis des Autors –auch für das ebenfalls sehr überzeugende Modell des Fraunhofer-Instituts für Techno- und Wirtschaftsmathematik ITWM (Anita Schöbel et al.); dieses Modell berücksichtigt auch die zeitlichen Verzögerungen zwischen der Corona-Übertragung und dem Ausbruch der Corona-Symptome.
Alle ernst zu nehmenden Modelliererinnen und Modellierer betonen, dass die Qualität der modellbasierten Vorhersagen sensibel von den jeweils verfügbaren Daten abhängt; deren Verfügbarkeit wird allerdings durchgängig als absolut unzureichend bezeichnet: Generell wird bedauert, dass die Nutzung des im Prinzip vorhandenen Datenmaterials (weltweite und regionale Daten über leichte und schwere Verläufe, in Abhängigkeit vom Alter und den Vorerkrankungen der Betroffenen, Einfluss der Impfungen usw.) für die Einbeziehung in die Modelle nicht oder kaum möglich war.
Differentialgleichungen modellieren das epidemische Geschehen eher makroskopisch, also gewissermaßen durch globale Betrachtung der Pandemieausbreitung, vergleichbar mit einer Strömung oder einer Flut. Vom Verhalten der einzelnen Individuen wird dabei abstrahiert. Daneben werden aber auch fundamental andere Modellierungsansätze verfolgt. Bei sogenannten „agentenbasierten“ Ansätzen wird z.B. versucht, das Verhalten und die Entscheidungen der einzelnen Individuen und die Auswirkungen dieser Entscheidungen auf das Gesamtsystem mathematisch zu erfassen. Ob diese Ansätze erfolgversprechender sind als die makroskopischen Ansätze, kann der Autor nicht fundiert beurteilen; er ist eher skeptisch.
Von Modellierern und Kommentatoren wird gelegentlich argumentiert, dass die politisch veranlassten Lockdown-Maßnahmen und Einschränkungen effektiver gewesen wären, wenn die Politik die Modellprognosen ernster genommen hätte. Das mag im Einzelfall zutreffen. Aber selbst bei intimer Kenntnis der zugrundeliegenden Mathematik ist eine objektive Bewertung der unterschiedlichen Modellansätze und Modellprognosen nicht einfach. Die Experten und Modellierer haben sich in vielen Fällen auch nicht einheitlich geäußert, es hat vielmehr – auch in Deutschland – eine problematische Lagerbildung unter den Modellierern gegeben. Besonders deutlich sind die unterschiedlichen Positionen und fragwürdigen Empfehlungen der Experten bei den Impfstrategien geworden – mit der Folge einer fatalen Verunsicherung der Öffentlichkeit.
Schließlich: Dass mathematische Modellierungsmöglichkeiten in Panik- und anderen Extremsituationen und Katastrophen an prinzipielle Grenzen kommen, dafür ist der überaus tragische Verlauf der Loveparade in Duisburg im Jahre 2010 ein erschütterndes Beispiel.
Stellungnahme zum AstraZeneca-Impfstopp aus statistischer Sicht
Das Paul-Ehrlich-Institut begründet den AstraZeneca-Impfstopp mit der Notwendigkeit, zu prüfen, ob zwischen den beobachteten Komplikationen und der Impfung ein kausaler Zusammenhang besteht. Aus statistischer Sicht ist der AstraZeneca-Impfstopp aber in jedem Fall die falsche Entscheidung. Auf der Basis der derzeit öffentlich bekannten Zahlen zu den AstraZeneca-Komplikationen ist das durch die Impfung entstehende Komplikations-Risiko bei weitem geringer als das bei Nicht-Impfung bestehende Risiko. Diese Feststellung gilt unabhängig von der Frage, ob die Komplikationen in einem kausalen Zusammenhang zur Impfung stehen oder nicht.
Statistische Ignoranz in Deutschland: lebensgefährlich
Statistische Ignoranz in Deutschland: lebensgefährlich
Statistik hat in Deutschland einen besonders schweren Stand, in der Schule und in der Öffentlichkeit.
Dabei könnte gerade jetzt, in diesen harten Corona-Zeiten, richtig verstandene Statistik ein
Minimum an Klarheit und Wahrheit in die Welt bringen. Und elementares statistisches Verständnis
der Öffentlichkeit könnte - zum Beispiel bei der Einschätzung von Risiken - eine echte Lebenshilfe für
alle sein.
Aber was wir jetzt im Zusammenhang mit dem Impfstoff AstraZeneca an Ignoranz erlebt haben und
noch erleben, ist skandalös. Da verbreitet irgendeine verantwortungslose Agentur, AstraZeneca habe
("möglicherweise") nur eine Wirksamkeit von 8 oder 10%, und mehrere Fernsehmoderatoren (auch
im WDR!) geben diesen statistischen Unsinn ungeprüft weiter. Dann setzt die Ständige
Impfkommission nach und entscheidet, dass der Impfstoff für Über-64-Jährige zunächst nicht
zugelassen wird. Anstatt sich über die internationalen Statistiken zu informieren, teilt der
Vorsitzende der Kommission mit, dass ihm die Datenlage nicht ausreicht, um den Impfstoff für alle
freizugeben.
Und dann wundert sich die Politik darüber, dass die Öffentlichkeit essentiell verunsichert ist und der
Impfstoff ungenutzt liegen bleibt. Wann endlich werden die für solche Fehlinformationen und
todbringenden Fehlentscheidungen Verantwortlichen zur Rechenschaft gezogen?
Goethe, Trump und die Mathematik
Zur Bedeutung der Mathematik in der digitalen Bildung
Goethe und Trump in einem Atemzug? Eines der größten literarischen Genies der Geschichte und die Inkarnation der aggressiven Ignoranz – die haben doch gar nichts gemeinsam, sollte man meinen. In einem Bereich leider doch: Beide hatten und haben ein sehr distanziertes Verhältnis zur Mathematik und zur mathematischen Wahrheit. Bei Trump, der in einer selbst geschaffenen narzisstischen Realität lebt, bedarf das vielleicht keiner genaueren Erläuterung, weil man weiß, wie er ganz allgemein mit der Wahrheit und mit Erkenntnissen der Naturwissenschaften umgeht. Aber Goethe – der mit seinen naturwissenschaftlichen Studien mehr Zeit verbracht hat als mit seiner Dichtung und dem zum Beispiel seine Farbenlehre besonders wichtig war? Die Elementarmathematik hat Goethe gelten lassen und wohl sogar geschätzt, aber über die „Höhere Mathematik“ und die Mathematiker (und Physiker) hat er gespottet: „Dass aber ein Mathematiker, aus dem Hexengewirr seiner Formeln heraus, zur Anschauung der Natur käme und Sinn und Verstand, unabhängig, wie ein gesunder Mensch brauchte, werd‘ ich wohl nicht erleben.“
Wir wollen der Frage, was Goethe zu dieser Geringschätzung der Mathematik veranlasst hat, hier nicht weiter nachgehen. Uns interessiert vielmehr die Frage, was heute los ist. Heute ist geradezu alles, was in der Welt an prinzipieller und an konkreter Erkenntnis gewonnen und an Innovation erreicht wird, wesentlich durch Mathematik geprägt: jede technische und naturwissenschaftliche Entwicklung, jedes Gerät, jeder Algorithmus hat zumindest auch eine mathematische Dimension. Das hat aber nicht etwa zur Folge, dass die heutigen Menschen in ihrer Mehrheit von der Mathematik fasziniert wären - bei den meisten, jedenfalls bei sehr vielen Menschen lösen mathematische Themen auch heute noch eher Unbehagen und unangenehme Erinnerungen an die Schule aus als Interesse und Begeisterung. Und auch heute erlebt man in der Öffentlichkeit, in TV-Shows, in den Medien, ja sogar in der Politik noch immer die augenzwinkernde Koketterie mit dem zur Schau gestellten und durch schlechte Schulleistungen nachgewiesenen Desinteresse an Mathematik.
Mathematik hat beides, die abstrakte und die angewandte Seite. Für viele Fachleute und Interessenten ist die abstrakte Seite der Mathematik von faszinierender Schönheit. Einer großen Öffentlichkeit hat sich die Schönheit der Mathematik aber gerade in Deutschland nicht vermittelt. Und das mag in der Tat damit zusammenhängen, dass die meisten Menschen im „Land der Dichter und Denker“ Schönheit eher in der Natur, in der Kunst und in der traditionellen Kultur suchen und finden - als in etwas scheinbar Unsinnlichem wie der Mathematik. Und dafür steht eben Goethe und nicht etwa Gauss – auch wenn Daniel Kehlmann mit „Die Vermessung der Welt“ Gauss ein Stück weit ins reale Leben geholt hat. Die Mathematik als Hochkultur, gar Liebe zur Mathematik – das scheint dann doch eher eine Emotion für einen kleinen Kreis von weltabgewandten Spezialisten zu sein.
Mit der angewandten Seite der Mathematik werden wir dagegen täglich durch eine Fülle naturwissenschaftlicher Erkenntnisse und Gesetzmäßigkeiten konfrontiert. Noch eindrücklicher erleben wir die angewandte Mathematik in diesen Jahren und Jahrzehnten aber in den rasanten Entwicklungen der Technik, insbesondere in der sich immer weiter beschleunigenden Digitalisierung. Die digitalen Entwicklungen bieten faszinierende Möglichkeiten der Zukunftsgestaltung, in allen technischen und ingenieurwissenschaftlichen Disziplinen und damit in einer auf vielfältige Weise innovativ geprägten Welt. Aber auch für die persönliche Lebensgestaltung und –vorsorge, etwa durch die individualisierte, datenintensive Medizin der Zukunft, deuten sich großartige Chancen an. Dass trotz dieser vielversprechenden Perspektiven die digitalen Entwicklungen ethisch und politisch gesteuert und rechtlich kontrolliert werden müssen, sollte gesellschaftlicher Konsens sein. Gerade in Deutschland haben aber die ängstlichen, überkritischen, bisweilen dystopischen Einschätzungen der Technologieentwicklung ein besonderes Gewicht– bis hin zum endzeitlichen Bild der Übernahme der Welt durch sich selbst weiterentwickelnde robotische Maschinen. Auch wenn die prinzipiell wertfreien Modelle der Mathematik dabei für beides stehen, für Utopie und Dystopie, sie werden vielen Menschen eher mit der düsteren als mit der beglückenden Zukunft assoziiert.
Dies sind Beschreibungen, keine Erklärungen für die sich von Mathematik distanzierende Koketterie, das Desinteresse, die Abneigung, den Hass auf die Mathematik. Was sind die Gründe? Ist es vielleicht der (schlechte) Mathematik-Unterricht, der eine positive Beziehung zur Mathematik in so vielen Fällen so nachhaltig stört? Tatsächlich gibt es viele hochkompetente und hochengagierte Mathematiklehrerinnen und –lehrer in deutschen Schulen. Andererseits hat der Autor es in seinen Seminaren und bei vielen anderen Gelegenheiten leider immer wieder erleben müssen, dass Lehrerinnen und Lehrer versuchen, den Schülerinnen und Schülern mathematische Zusammenhänge zu „erklären“, die sie selbst nicht verstanden haben. Solche gravierenden Fehler werden oft nur von hochbegabten Schülerinnen und Schülern durchschaut.
Auch in diesen Jahren und Tagen spielt das Thema „mathematische Bildung“ wieder eine aktuelle Rolle. Es kommt über die digitale Bildung ins Spiel. Digitale Bildung, darüber sind sich alle Akteure einig, ist eins der wichtigsten politischen Ziele überhaupt, Deutschland hat hier einen extremen Nachholbedarf. Aber sofort stellt sich die Frage: Was sind denn die Ziele der digitalen Bildung? Wofür sollen die Milliarden €, die seit einigen Jahren den Ministerien, Schulen, Lehrerinnen und Lehrern zur Verfügung stehen, denn ausgegeben werden? Eine einfache (und richtige) Antwort ist: für Vernetzung, für die Ausstattung mit Hardware – darüber wird man sich schnell einig (auch wenn sich die Beschaffung als solche dann vielleicht über Jahre hinzieht und die Geräte schnell wieder veralten). Aber dann? Was sind dann – wenn die Ausstattung vorhanden ist und die Arbeit anfangen kann – die Inhalte des digitalen Unterrichts? Öffentlich diskutierte Ziele sind insbesondere: Medienkompetenz, Programmierkenntnisse, Grundlagen der Informatik usw. – und immer wieder Medienkompetenz. Von mathematischen Inhalten ist in der öffentlichen und politischen Diskussion kaum die Rede.
Die Substanz alles Digitalen sind die Algorithmen. Aber dass Algorithmen immer auch einen mathematischen Kern haben, wird so deutlich nicht gesagt. Kurios ist, dass gerade in Deutschland Informatik ein sehr positives Image hat, Mathematik aber ein überwiegend negatives. Sachlich ist das nicht begründet: Informatik und Mathematik haben einen großen Überlappungsbereich. Einige meiner führenden Kollegen machen gar keinen Unterschied zwischen den beiden Disziplinen. Und tatsächlich sind es gerade die Algorithmen, von denen man oft gar nicht sagen kann, ob sie eher der Mathematik oder der Informatik zuzuordnen sind. Gerade in den neuesten Entwicklungen wachsen zum Beispiel Algorithmen, die eher mit Daten umgehen und daher traditionell eher der Informatik zugeordnet werden, und Algorithmen, in denen überwiegend gerechnet wird und die daher eher der Mathematik zugeordnet werden, methodisch immer stärker zusammen. Die Algorithmen der Künstlichen Intelligenz und des Maschinellen Lernens sind dafür besonders markante Beispiele.
Insofern eröffnet die systematische Beschäftigung mit den grundlegenden Prinzipien traditioneller und aktueller Algorithmen eine große Chance, die Mathematik von ihrem negativen Image zu befreien und Mathematik und Informatik als zwei Seiten einer Medaille zu begreifen. Und wenn dieses Zusammenspiel schon in der Schule praktiziert und verstanden wird, hat Deutschland auch eine Chance, methodisch Anschluss an die internationale digitale Entwicklung zu finden.
Q16 Quanten und Qubits - Was man so liest
Von Bernhard Thomas und Ulrich Trottenberg
Quanten-Computing wird in den Medien, aber auch in Vorträgen und in der Fachliteratur mit einer Reihe von Aussagen charakterisiert, die als Sprachkonstrukte ziemlich exotisch klingen - nach einer anderen Welt, in der logisch Unmögliches möglich scheint. Wir wollen uns einige dieser Sprachfiguren ansehen und überlegen, was dahinter steckt.
Unsere bisherigen Blog-Abschnitte über Qubit-Algorithmen sollten ausreichen, hier ein klares Verständnis zu schaffen. Hier die Übersicht über die Aussagen.
"Quanten können 0 und 1 gleichzeitig sein"
"Mit n Qubits kann man 2**n Zahlen gleichzeitig darstellen"
"Für N Zahlen benötigt ein Quanten-Computer nur log(N) Qubits"
"Ein Quanten-Computer kann mehrere Berechnungen gleichzeitig durchführen (Quanten-Parallelismus)"
"Was auf herkömmlichen Rechner Jahre dauert, kann ein Quanten-Rechner in Sekunden erledigen (Exponentielle Beschleunigung)"
"Quanten-Rechner werden herkömmlichen Rechnern überlegen sein (Quanten-Supremacy)"
"Jedes zusätzlich Qubit verdoppelt die Leistungsfähigkeit des Systems"
"Quanten können 0 und 1 gleichzeitig sein"
Dieser Satz und Abwandlungen davon ziehen sich durch die Quanten-Computing-Literatur wie ein Mantra des QC. Auch wenn er gelegentlich nur als Metapher gesehen wird, suggeriert dieser Satz in der öffentlichen Diskussion eine mystische Eigenschaft der Quanten, nicht zuletzt illustriert durch das Bild von Schrödingers Katze, die "gleichzeitig tot und lebendig" ist.
Damit werden auch die informatischen Gegenstücke der Bits, die Qubits, charakterisiert. Im Gegensatz zu Bits, die nur "0 oder 1" sein können, können Qubits "0 und 1 gleichzeitig" sein.
Wie könnten wir das feststellen? Wir wissen, dass die Messung eines Qubits entweder 0 oder 1 ergeben kann, aber nicht beides. Wenn wir mehrfach messen, bekommen wir manchmal eine 0, manchmal eine 1 als Ergebnis, aber nie "gleichzeitig". Was kann also gemeint sein - wenn es überhaupt einen Sinn ergibt.
Es gibt Varianten dieser "Gleichzeitig"-Sprachfigur, die etwas tiefergehend klingen: "Quanten können verschiedene Zustände gleichzeitig einnehmen". Wir wissen, dass man Zustände von Systemen in Form von mathematisch eindeutigen Ausdrücken beschreiben kann - so auch Qubits und Qubit-Systeme. Ausgehend von einem Anfangszustand sahen wir, wie mittels Qubit-Operationen (oder Gates) ein Qubit-Zustand in einen nächsten überführt werden kann. Zu jedem Zeitpunkt ist der Zustand des Qubits daher eindeutig festgelegt. Wenn wir nicht unsere normale zweiwertige Logik (2 Wahrheitswerte: wahr, falsch - oder 0, 1) in Frage stellen, kann ein Qubit nicht zwei verschiedene Zustände gleichzeitig haben. Eine Zahl, ein mathematischer Ausdruck, der einben Zustand beschreibt, kann nicht gleichzeitig 0 und 1 sein: z = 0 = 1?
Manchmal findet man Texte, in denen das "Gleichzeitige" durch die "Superpostion" ergänzt wird: "Quanten können in einer Superosition von 0 und 1 gleichzeitig sein". Wir wissen, was eine Superpostion ist. Z.B. ist 1/√2 (|0>+|1>), die Hadamard-Operation auf den Basiszustand |0>, eine Superpostion (oder mathematisch: Linearkombination) der Qubit-Zustände |0> und |1>. Wir haben Qubit-Zustände meist in Form von x-y-Koordinaten eines Punktes auf dem Einheitskreis beschrieben - im Beispiel also (1/√2,1/√2). Somit können wir korrekt formulieren: Ein Qubitzustand hat zwei Koordinaten. Aber was heißt dann "gleichzeitig"? Wenn jemand in Ingolstadt ist, befindet er sich z.B. auf der Strecke von München nach Nürnberg - aber ist er (möglicherweise) in München und Nürnberg "gleichzeitig"?
Wenn auch die Redewendung "... kann 0 und 1 gleichzeitig sein" etwas Unsinniges suggeriert, können wir sie als solche akzeptieren, wenn man sie auf die Möglichkeit einer Superposition von zwei (Basis-)Zuständen eines Qubits zurückführt. Darin unterscheiden sich Qubits und Bits tatsächlich.
Und während ein Bit nur einen der beiden Zustände 0 oder 1 repräsentieren kann (siehe BIT-Box in Q3), kann ein Qubit einen Zustand aus einer unendlichen Menge von Superpositionszuständen annehmen. Wobei wir das "unendlich" im Sinne aller Punkte auf dem Einheitskreis verstehen, ohne zu fragen, ob wirklich unendlich viele Superpositionen realisierbar sind (technisch und quantenmechanisch).
Eine elegante und gleichzeitig korrekte, einfache Erklärung finden wir im Glossar der IBM (Übersetzung DeepL):
Ein Qubit (ausgesprochen "kju-bit" und kurz für Quantenbit) ist der physikalische Träger der Quanteninformation. Es ist die Quantenversion eines Bits, und sein Quantenzustand kann Werte von |0> , |1> oder die Linearkombination von beiden annehmen, was ein Phänomen ist, das als Superposition bekannt ist.
Mehr ist eigentlich nicht zu sagen.
"Mit n Qubits kann man 2**n Zahlen gleichzeitig darstellen"
Mit n Bits kann man zwar auch 2**n verschiedene Zahlen darstellen - gemeint sind Binärzahlen in Form von Bitketten - aber immer nur eine zu einem Zeitpunkt, z.B. im Speicher eines klassischen Computers.
Diese Aussage zusammen mit dem "Quantenparallelismus" (s.u.) soll die überragende Leistungsfähigkeit von Quanten-Computern deutlich machen. Man liest auch: "Mit jedem weiteren Qubit verdoppelt sich die Kapazität" und "Schon 300 Qubits können mehr Werte speichern, als das bekannte Universum Teilchen enthält".
Nun ja, wie soll man das verstehen? Zunächst zu den beiden letzten Versionen des "Kapazitätssatzes": Auch mit jedem weiteren Bit verdoppeln sich die möglichen Werte, die man speichern - und wieder lesen - kann. Immer einer zu einer Zeit (Schreib-Lese-Zyklus). Und mit 300 Bits kann man mehr als alle Teilchen des bekannten Universums abzählen, oder je eine Zahl zu einem Zeitpunkt im Bereich 0 bis 2**300-1 speichern. Bei Qubits liegt das Geheimnis offenbar wieder im "gleichzeitig". Wieder nur eine Metapher?
Ein System von n Qubits, z.B. n=3, befindet sich zu einem Zeitpunkt in einem Zustand (von prinzipiell unendlich vielen), der eine Linearkombination (Superposition) von nunmehr 2**n Basiszuständen ist, also 8 bei n=3. In der ket-Schreibweise tritt jede n-lange Bitkette als ein Basiszustand auf, bei n=3 also |000>, |001>, |010>, |011>, |100>, |101>, |110>, |111>. Bei n = 300 sind es halt ......
Denken wir an Koordinatensysteme, wie z.B. in Q11, dann haben wir ein 8-dimensionales Koordinatensystem und jeder 3-Qubit-Zustand wird durch 8 Koordinaten beschrieben. "Gleichzeitig" - für einen Punkt braucht man 8 Koordinaten "gleichzeitig".
Kann man in einer Superposition von 2**n Basiszuständen das gleichzeitige Speichern von 2**n Zahlen sehen? Nehmen wir eine gleichmäßige (uniforme) Superposition, d.h. alle Basiszustände kommen mit dem gleichen Koeffizienten vor. Bei n=3 also mit 1/√8.
Speichern nützt nur dann etwas, wenn man mit dem Gespeicherten etwas anfangen kann, z.B. weiter verarbeiten mittels Qubit-Operationen oder Lesen, d.h. Messen. Beim Weiterverabeiten zu einem neuen Zustand können tatsächlich alle Komponenten der Linearkombination in einer Operation berücksichtigt werden (Quantenparallelismus, s.u.). Beim Messen (gegen die Basiszustände) erhält man eine Häufigkeitsverteilung über alle Bitketten, die als Basiszustände in der aktuellen Superposition vertreten sind. Sind einige nicht vertreten, tauschen sie, bis auf Quantenfehler, auch nicht im Messergebnis auf.
Aber was machen wir damit? Welche Information ziehen wir daraus? Dass 2**n Bitketten beim Messen auftreten können, wussten wir schon vorher. Wir "lesen" also nichts Neues. Wenn wir 2**300 Teilchen mit unterschiedlichen Bitketten versehen wollten, konnten wir das auch schon ohne Quanten-Computer (QC).
Wo liegt also die Information, die wir durch die Quanten-Berechnung gewonnen haben? Wohl in der gemessenen Häufigkeitsverteilung:
- Wir schauen nur auf "vorhanden" und "nicht vorhanden" von gemessenen Bitketten. Eine häufige Form der Interpretation von QC-Ergebnissen, z.B. beim Herausfinden eines Orakels, wie im Bernstein-Vazirani Problem oder dem von Deutsch-Josza. Man kann sich das so vorstellen: Der Qubit-Algorithmus "rechnet" mit den 2**n Basiszuständen des n-Qubit Systems, der Ergebnis-Zustand enthält aber in nur einen Basiszustand, der dann bei der Messung eine ziemlich eindeutige Bitkette liefert. Eine solche Methode ist auch die sogenannte Amplituden-Verstärkung (amplitude amplification). Zum Auffinden einer bestimmten Bitkette beginnt man mit einer uniformen Superposition und verändert diesen Zustand Schritt für Schritt so, dass die Amplitude des Basiszustands mit der gesuchten Bitkette zunehmend "größer" wird. Die Iteration wird beendet, wenn man nahe genug an der gesuchten Bitkette ist, d.h. wenn beim Messen diese Bitkette eine überragende Wahrscheinlichkeit erreicht. Das Verfahren wird auch Grover-Iteration genannt.
- Uns interessiert ein "numerisches" Ergebnis, z.B. eine Zahl oder eine Reihe von Zahlen (Vektor), die sich bei der Messung am Ende der Rechnung als Häufigkeiten bestimmter Bitketten ergeben. Als "numerisches" Ergebnis nimmt man dann die Liste dieser Häufigkeiten. Hier stoßen wir aber auf verschiedene Probleme. Eines davon ist, dass ein echter QC die Häufigkeiten nicht exakt misst. Um halbwegs brauchbare Werte abzuleiten, müssen wir das QC Programm wiederholt durchlaufen lassen. Wie oft? Für n=3 kann man das ja einmal ausprobieren mit dem IBM QC. Wie oft bei n=50 oder n=300?
"Für N Zahlen benötigt ein Quanten-Computer nur log(N) Qubits"
Dies ist eine Variante der vorigen Aussage und besagt: "Während man auf herkömmlichen Computern für N Zahlen auch N Speicherplätze benötigt, braucht ein Quanten-Computer nur log(N) Qubits". Man hat also, umgekehrt gesehen, einen exponentiellen Effekt. Und damit ist ein Quanten-Computer exponentiell leistungsfähiger als ein herkömmlicher. Wie auch immer das gemeint ist, es läuft darauf hinaus, dass man eine Überlagerung der N Basiszustände eines "log(N) großen" Qubit-Systems herstellt, bei der die Koeffizienten (auch Amplituden genannt) gerade die gewünschten N Zahlen sind. Wenn man also weiß, wie, kann man einen solchen Superpositionszustand als "Input" herstellen, und einen Qubit-Algorithmus damit weiterrechnen lassen. Das ist das sog. Amplituden-Verfahren oder auch Amplituden Encoding.
Aber halt! Die N Amplituden müssen ja in der Summe der Quadrate 1 ergeben. Schränkt das nicht die freie Wählbarkeit der N Zahlen ein? Nicht wirklich - man muss nur vorher jede Zahl durch die Summe aller Quadrate teilen, genauer, durch die Quadratwurzel dieser Summe. Damit kann man dann "Quanten-Rechnen". Allerdings tritt bei der Ergebnis-Festellung wieder das Problem aus 2. auf.
Um die N Zahlen als Input verwenden zu können, muss man zu Beginn des Qubit-Algorithmus geeignete Qubit-Operationen (Gates) ausführen, so dass sie in einer Superposition zu Koeffizienten von Basiszuständen werden. Das kann trotz "Quantenparallelität" aufwendig sein. Hier ein Beispiel:
Angenommen, wir wollen die 4 Zahlen 1.0, 1.0, √2 = 1.414, 2.0 als Input in Form von Amplituden für ein 2-Qubit-System bereitstellen (N=4, n=2). Die Summe der Quandrate ist 1.0+1.0+2.0+4.0 = 8.0. Die Wurzel daraus ist √8. Dadurch müssen wir die 4 Zahlen teilen, damit diese eine gültige 2-Qubit Superposition ermöglichen: 1/√8, 1/√8, 1/√4, 1/√2. Es ist damit z.B. der Zustand 1/√8 |00> + 1/√8 |01> + 1/√4 |10> + 1/√2 |11> durch einen Qubit-Circuit herstellbar. Wie geht das? Hier ist eine Lösung:


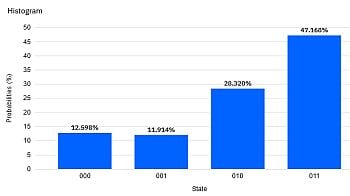
Das "Fine-Tuning" der Amplituden erfolgt hier mittels Drehungen (Ry). Der resultierende Zustand ist verschränkt, d.h. er kann nicht als Kombination der einzelnen Qubits hergestellt werden. Das kann man nach der Methode in Q9 nachprüfen. (Ergebnis eines Simulatorlaufs mit 1024 shots.)
"Ein Quanten-Computer kann mehrere Berechnungen gleichzeitig durchführen"
Diese Aussage wird häufig als Verdeutlichung des sog. Quanten-Parallelismus verwendet. Auch hier wird wieder das Mantra-Wort "gleichzeitig" verwendet, dieses Mal aber in einer sinnvollen Bedeutung, nämlich im Gegensatz zu "nacheinander" (sequentiell). Natürlich können auch herkömmliche Computer heutzutage mehrere Berechnungen zeitlich parallel ausführen. Der Unterschied ist aber technisch fundamental: Herkömmliche Parallelrechner (z.B. MIMD-Architekturen) führen mehrere, durchaus auch verschiedene, Computerbefehle (Instructions) zur gleichen Zeit aus und verwenden dabei u.U. unterschiedliche Daten als Input.
Quanten-Computer führen zu einem Zeitpunkt einen Befehl (in Form von Gates) auf einer Datenstruktur aus. Die Datenstruktur ist der aktuelle Zustand eines n-Qubit-Systems, also meist eine Superposition oder gar eine Verschränkung. Der Zustand eines n-Qubit-Systems kann aber, wie wir zuvor gesehen haben, bis zu N=2**n Zahlen (in Form von Amplituden) repräsentieren. Indem der Qubit-Befehl auf den Zustand wirkt, wirkt er simultan auf alle Basiszustände, die in der Superposition vorkommen. Als Ergebnis können sich damit simultan alle Amplituden der Basiszustände verändern. Bingo!
Mathematisch gesehen ist das überhaupt nichts Ungewöhnliches. Eine Matrix A "wirkt" bei Multiplikation mit einem Vektor x auf alle seine Komponenten "gleichzeitig": y= Ax (Lineare Algebra). Wird ein Punkt (x,y) mittels einer Funktion F verschoben, dann werden alle Koordinaten "gleichzeitig" verschoben: (u,v) = F(x.y). Und auch die Qubit-Operatoren (Gates) können mathematisch als Matrizen dargestellt und verwendet werden. Wenn es allerdings ans praktische Rechnen geht, etwa mit einem Algorithmus, der die Matrixmultiplikation explizit durchführt, dann geht es klassisch (auf einem herkömmlichen Rechner) wieder nur Schritt für Schritt: die Operation wird in viele Einzelschritte zerlegt, die nacheinander ausgeführt werden. Hier unterscheiden sich klassische und Quanten-Computer tatsächlich fundamental. Quanten-Computer, wie die von IBM, sind technisch so aufgebaut, dass sie eine komplette Superposition in einem, statt in vielen Schritten verarbeiten können.
Wie man sich das vorstellen kann, zeigen wir an einem einfachen Beispiel: Das exklusive Oder (XOR) von zwei Bits entspricht der einfachen Bit-Addition bis auf die Operation "1+1", die 0 ergibt statt 2. (Dafür verwendet man auch das Symbol ⊕ statt +). Wir können die Bit-weise XOR-Berechnung auch als Qubit-Circuit durchführen. Das ergibt die 4 Auswertungen in der Abbildung, wobei jeweils q0 und q1 auf Zustand 0 bzw. 1 gesetzt werden und das Ergebnis den neuen Zustand von q1 ergibt.
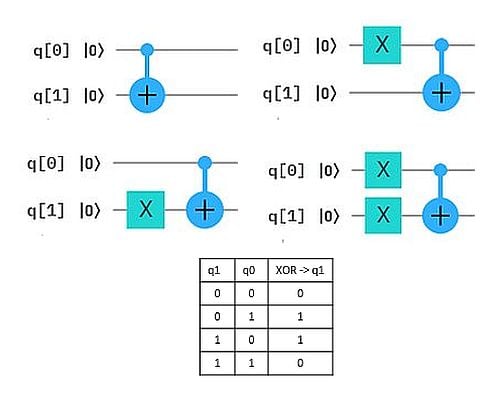
Quanten-Parallelismus ermöglicht aber Superpositionen statt einzelner Basiszustände als Input zu präparieren, typischerweise mit dem H-Gate (Hadamard-Gate). Damit muss die Berechnung nur einmal ausgeführt werden und wir erhalten alle 4 Ergebnisse auf einmal.
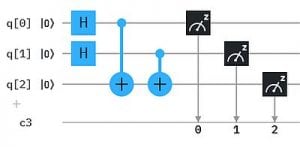
Um die Ergebnisse einfacher "lesen" zu können, haben wir hier das XOR Ergebnis auf ein drittes Qubit q2 übertragen. So erhalten wir als Messergebnis genau die obige XOR Tabelle mit XOR -> q2 : 000, 101, 110, 011 (q2 steht hier wieder jeweils ganz links in der Bitkette).
"Was auf herkömmlichen Rechnern Jahre dauert, kann ein Quanten-Rechner in Sekunden erledigen"
Als Begründung liest man dabei oft, dass Quantenrechner "exponentiell schneller" rechnen können als herkommliche. Was bedeutet das?
Das heißt zum Beispiel folgendes: Wenn wenn wir zwei Methoden haben, die eine Aufgabe lösen, etwa eine Berechnung durchführen oder ein "Geheimnis" (Q15) zu finden, und die eine Methode benötigt N Zeiteinheiten oder Rechenschritte, die andere aber nur log(N) viele, dann stellt die zweite Methode eine exponentielle Verbesserung - oder Beschleunigung - gegenüber der ersten dar. (Denn, für k=log(N) ist N=exp(k).)
Es gibt eine ganze Reihe von solchen "Beschleunigungsbeziehungen" zwischen Methoden zur Lösung gleicher Aufgaben. Der Grover Qubit-Algorithmus benötigt nur etwa √N Schritte gegenüber N Schritten bei der klassischen Methode. Hier haben wir also eine quadratische Beschleunigung. In Q15 hatten wir das am Beispiel des Bernstein-Vazirani-Algorithmus diskutiert.
Solche Beschleunigungen gibt es von je her auch im klassischen Computing als Effekt einer algorithmischen Verbesserung. So gibt es z.B. unterschiedliche Sortier-Algorithmen, die sich bezüglich ihres Rechenaufwands erheblich unterscheiden, oder auch Verfahren zur numerischen Simulation, bei denen sogenannte Mehrgitterverfahren große Beschleunigungsraten bringen.
Der tatsächliche Beschleunigungseffekt des Quanten-Computing gegenüber herkömmlichen Bit-Computing beruht auf einer Kombination von zwei Dingen: dem Quanten-Parallelismus der Hardware (s. voriger Abschnitt) und dem Algorithmus, der für Qubits konstruiert werden kann.
Ein Rechenbeispiel: Hätte man eine (hypothetische) Aufgabe, die auf einem gewöhnlichen Rechner mit dem schnellsten Algorithmus 10 Jahre dauern würde, dann würde eine exponentielle Beschleunigung auf einen Zeitaufwand von rund 20 Sekunden führen: log(10*360*24*60*60) = log(311040000) = 19,56. Diese Zahlen sind allerdings eher fiktiv, da wie keine konkrete Aufgabe vor Augen haben und Wiederholungen und anderen "Overhead" nicht berücksichtigen. Aber es zeigt, wie sich die Größenordnung ändern.
Hätten wir also eine Aufgabe, die herkömmlich Jahre dauern würde, und hätten wir dazu ein Quanten-Computer, der sie alternativ mit exponentieller Beschleunigung löst, könnten wir die Aussage so akzeptieren. Allerdings gibt es noch nicht viele Algorithmen für Quanten-Computer, die in dieser Form praktische verwendbar sind. Was nicht zuletzt auch an der Größe und "Sensibilität" heutiger QC liegt.
Ein relevantes Beispiel, das immer wieder als "Gefahr durch Quanten-Computer" zitiert wird, ist das Verfahren von Shor, mit dem man einen wichtigen Schritt beim "Knacken" von besten heutigen Verschlüsselungsverfahren in akzeptabler Zeit durchführen kann. Um das zu verstehen, braucht es aber schon mehr Einsicht in die zugrunde liegende Mathematik. Daher wird hier meist nur der (befürchtete) Effekt zitiert und auf Verständnis verzichtet.
"Quanten-Rechner werden herkömmlichen Rechnern überlegen sein"
Man spricht auch generell von Quanten-Überlegenheit (Quantum Supremacy). Trotz der beängstigent klingenden Bezeichnung handelt es sich hier um eine unspektakuläre Sache. Es bedeutet lediglich das Ereignis, dass es eine Berechnung gibt, die ein Quanten-Computer schneller als jeder herkömmliche Supercomputer durchführen kann. Dabei ist es erst einmal egal, ob diese Berechnung einen Sinn macht oder praktische Bedeutung hat. Wie man kürzlich lesen konnte, hat man (mit einem QC von Google) bereits eine solche Berechnung durchführen können, d.h. der Meilenstein Quantum Supremacy ist schon erreicht.
"Jedes zusätzlich Qubit verdoppelt die Leistungsfähigkeit des Systems"
Hier bleibt einerseits unklar, was mit Leistungsfähigkeit gemeint ist - Rechenleistung, Speicherleistung, Leistung eines Algorithmus, der ein Qubit mehr zur Verfügung hat? Auch wenn wir einen Bit-Speicher (Register) um ein Bit erweitern, also von n auf n+1 Bits, können wir damit 2**(n+1) = 2*2**n Werte speichern bzw. mehr oder längere Befehle ausführen. So hatte sich auch die Prozessorarchitektur von früheren 32 Bit auf 64 Bit bei herkömmlichen Computern verändert und dabei prinzipiell eine 32-fache Verdoppelung der Leistung ermöglicht.
Was macht nun ein Qubit mehr aus bei einem Quanten-Computer? Zum einen gibt es dann doppelt so viele Basiszustände. Z.B. von 8 bei einem 3-Qubit System auf 16 bei 4 Qubits. In Superposition können damit 16 statt nur 8 Koeffizienten (Amplituden) einen Zustand bestimmen. Diese Verdoppelung ist analog der Situation bei Bits und wir hatten das schon oben bei N vs log(N) erklärt.
Zum anderen wissen wir, dass - ganz ander als beim Bit-Computing - verschränkte Zustände eine wichtige Rolle im Qubit-Computing spielen. Man kann sich also fragen, was bringt ein zusätzliches Qubit für die möglichen Verschränkungen, oder allgemein für die möglichen "Konfigurationen" von Superpositionen. Anders ausgedrückt: wieviel mehr Möglichkeiten gibt es für Zustände, in denen nur ein Basiszustand vertreten ist, oder zwei, oder drei usw. - unabhängig von den Werten der Amplituden. Diese Zahl wächst offenbar kombinatorisch. Für n=2 sind die "Muster" noch überschaubar: 4 mal |x>, 6 mal |x>+|y>, 3 mal |x>+|y>+|z> und 1 mal |x>+|y>+|z>+|v>, wenn |x>,|y>,|z>,|v> die Basiszustände |00>, |01>,|10>,|11> durchlaufen.
In Q13 (Superdichte Codierung) haben wir einen anderen Verdopplungseffekt gesehen: die Kapazität, Bitketten in GHZ-verschränkten Qubits zu "speichern" bzw. zu übertragen. Hier brachte jedes weitere Qubit in einer solchen Verschränkung eine Verdoppelung der Anzahl übertragbarer Bitketten.
Zuletzt eine Anmerkung: Bei "Was man so liest" fragt man sich leicht, wo man das gelesen hat. Die konkreten Aussagen in den Überschriften sind keine echten Zitate, obwohl sie so oder in Variationen der Wortwahl tatsächlich vorkommen. Wir wollen hier aber kein "Bashing" anzetteln, sondern nur kostruktiv klären, was dahinter steckt oder wo man leicht fehlgeleitet wird. Daher verzichten wir auf Quellenangaben.
Quantencomputing ohne Quantenmechanik?
Von Ulrich Trottenberg und Bernhard Thomas

Quantencomputing ist ein heißes Thema - in Universitäten, Forschungszentren, in den großen IT-Firmen, in der internationalen und nationalen Forschungsförderung - und mittlerweile auch in der Politik. Das geht so weit, dass uns führende Personen der Öffentlichkeit, die sonst mit ihren schwachen mathematischen Leistungen und ihrem mathematischen Desinteresse kokettieren, uns das Quantencomputing mit seinen großartigen, revolutionären Möglichkeiten „erklären“.
Auf der anderen Seite haben uns die bedeutendsten Physiker des letzten Jahrhunderts erklärt, dass man die Quantenmechanik - also die physikalische Basis des Quantencomputing – wenn überhaupt, nur mathematisch verstehen kann: Zentrale Phänomene der Quantenmechanik, insbesondere die Superposition und die Verschränkung, entziehen sich der Anschauung und stehen in (scheinbarem) Widerspruch zur physikalischen Alltagserfahrung. Selbst Albert Einstein bezeichnete das Phänomen der Quanten-Verschränkung als spukhafte Fernwirkung, der ebenfalls geniale Physiker Richard Feynman formulierte pointiert: „Man kann sicher sagen, niemand versteht die Quantenmechanik.“ Und Erwin Schrödinger, einer der Begründer der Quantenmechanik, versuchte mit seinem berühmten Katzen-Paradox in einem oft missverstandenen Gedankenexperiment die Übertragung quantenmechanischer Phänomene auf die Alltagswelt ad absurdum zu führen (Siehe "Schrödingers Katze" bei Wikipedia).
Und die echten Experten des Quantencomputing? Was sagen die? Da überwiegen in der Tat die optimistischen Einschätzungen (nicht nur bei denen, die von den Forschungsmilliarden gefördert werden). Sie gehen z. B. davon aus, dass man mit Quantencomputern - bei einer Reihe wichtiger Anwendungen - viel, viel schneller, „exponentiell“ schneller rechnen kann als mit herkömmlichen Computern, dass man mit Quantencomputern Probleme lösen kann, die als praktisch unlösbar gelten, fast jeden Verschlüsselungscode knacken kann usw. .
Aber es gibt auch die Skeptiker, die noch einen weiten Weg vor sich sehen bis zu einer praktischen Realisierung großer, leistungsfähiger Quantencomputer. Ein Argument der Skeptiker ist auch, dass mit Quantencomputern erzielte Ergebnisse in aller Regel nur mit einer gewissen Wahrscheinlichkeit „richtig“ sind und dass man möglicherweise die Rechnungen sehr häufig wiederholen muss, um die Ergebnisse abzusichern.
Schließlich die Algorithmen, die Software? Gibt es die denn schon? Kann man die entsprechenden Algorithmen verstehen? Die Interscience Akademie für Algorithmik hat den Versuch gemacht, Quanten-Algorithmen verständlich zu machen mit nicht mehr als Schulmathematik (Unterstufe / Mittelstufe). Daraus ist eine Serie von 16 Blogs entstanden, eingeleitet durch den Artikel "Quanten-Computing für die Schule - Echt jetzt?". Das geht ohne die Quantenmechanik zu bemühen – und auch ohne die quantenmechanische Mathematik (wie Hilberträume, partielle Differentialgleichungen, Tensoren, Matrizen und Vektoren usw.) zu verwenden. Was vorausgesetzt wird, ist ein bisschen Schulmathematik, einfaches Grundverständnis für klassische Computer; nützlich beim Ausprobieren, aber nicht notwendig, sind elementare Programmierkenntnisse.
Viel Spaß beim Quantencomputing!
Quanten-Computing für die Schule - Echt jetzt?
Von Bernhard Thomas und Ulrich Trottenberg
Kann man Quanten-Computing als Thema im Schulunterricht behandeln? Die erste schnelle Antwort wird sein: sicher nicht! Die physikalischen Grundlagen, die Mathematik dazu übersteigt unsere Vorstellungskraft und jegliches Wissen, das man im Rahmen von Schule vermitteln bzw. erwerben kann, sei es im Physikunterricht, in Mathematik oder im Informatikunterricht. Andererseits hört und liest man seit einiger Zeit viel über das Potenzial zukünftiger Quantencomputer - übertroffen nur noch von der Diskussion über Künstliche Intelligenz.
Dem Quanten-Computing, genauso wie dem "klassischen" Computing, liegen Algorithmen zugrunde. Wenn wir uns auf das Algorithmische des Quanten-Computing beschränken, kann es uns dennoch gelingen - etwa im Rahmen des Informatikunterrichts - auch Algorithmen aus der "Quanten-Welt" (Qubit-Algorithmen) kennen zu lernen, zu verstehen und sogar zu konstruieren. Und, was das Ganze besonders spannend macht, auch auf den ersten echten Quantencomputern laufen zu lassen! Auch bei herkömmlichen Computern verstehen wir ja die Physik nicht wirklich, können aber dennoch schon Grundschülerinnen und Grundschülern erklären, wie man grafische Programme erstellt, die dann auf Computern oder kleinen Robots laufen. (Siehe Open Roberta, Calliope, Scratch usw.)
Die Q Blog-Serie der Interscience Akademie für Algorithmik
Unsere Q Blog-Serie ist primär gedacht als Information, Material und Anregung für Lehrpersonen oder interessierte Schülerinnen und Schüler. Es gibt aber auch einiges für jeden zu entdecken, der immer schon einmal wissen wollte, was das Besondere an den geheimnisvollen Qubit-Algorithmen und ihren viel gerühmten Eigenschaften ist. Denn tatsächlich - einiges ist anders als man es von herkömmlichen Algorithmen gewohnt ist.
Schulwissen
Wir werden sehen, dass wir uns in dieser Serie auf allgemeines Schulwissen beschränken können. D.h. wir kommen zum Einen ohne Kenntnisse der Quantenphysik aus, wenngleich die meisten Ideen und Konzepte der Quanten-Informatik und der Qubit-Algorithmen aus der Quantenphysik abgeleitet sind, und zwar insbesondere aus der Mathematik der Quantenphysik. Dort haben sie auch ihre Entsprechung, sogar ihre Umsetzung, in Form von Quanten-Computern. Der Respekt vor diesem immensen mathematisch-naturwissenschaftlichen Wissen seit den Anfängen des letzten Jahrhunderts kann nicht groß genug sein, Respekt gebührt vor allem denen, die sich seit etwa den 1980er Jahren mit der informatischen Bedeutung der Quantenphysik befasst haben und befassen. Auch hier ist der Schatz an dokumentiertem Wissen heute unüberschaubar. Was aber nicht bedeutet, dass man aus Ehr-Furcht davor keinen Zugang zu diesen Dingen finden kann.
Zum anderen wollen wir ohne die "höhere Mathematik" auskommen. Wir verzichten auf Hilbert-Räume, Vektoren und Matrizen, Tensor-Rechnung, komplexe Zahlen, partielle Differentialgleichungen - das übliche Handwerkszeug professioneller Quanten-Mathematiker und-Informatiker. Was wir verwenden, ist bewusst eher mittleres Schul-Niveau: die Darstellung von Punkten im Koordinatensystem, den Einheitskreis im Koordinatensystem, ab und an den "Pythagoras", Prozentrechnung und relative Häufigkeiten, auch mal den Sinus oder Cosinus, wenn's hoch kommt - und was wir brauchen, ist Offenheit für neue Entdeckungen.
Zugegeben, wir werden damit nicht die gesamte Quanten-Informatik und ihr algorithmisches Instrumentarium darstellen können. Aber wir werden mit unseren Mitteln die Grundprinzipien von Qubits und Qubit-Algorithmen verstehen, einfache bis namhafte komplexere Algorithmen kennenlernen und dabei viele der mit Qubits verbundenen Begriffe und Eigenschaften entmystifizieren. Und auch der korrekte, sinnvolle Sprachgebrauch der Qubit-Welt will eingeübt werden.
Entdecken statt Auswendiglernen
Auch in der Darstellung des Themas Qubit-Algorithmen gehen wir einen etwas anderen Weg. Statt mit den üblichen Definitionen loszulegen, gehen wir hier auf Entdeckungstour. Unter anderem die grundlegenden Modelle – vom Bit bis zum Qubit – entwickeln wir anhand von “virtuellen Experimenten”. Die allerdings nichts mit Quantenphysik zu tun haben. Natürlich "lernt" man dabei auch Neues, das man sich merken sollte - aber dafür gibt es Beispiele "zum Anfassen", damit das leichter fällt.
Qubits oder Quanten?
Warum sprechen wir von Qubit-Algorithmen und nicht von Quanten-Algorithmen? Qubits sind die "Objekte" der Quanten-Informatik und der Algorithmen, die wir hier besprechen. Man kann sie erst einmal als Entsprechung zu klassischen Bits verstehen. Sie sind im Prinzip völlig unabhängig von dem, was "Quanten" bedeutet - bis auf die Tatsache, dass man sie am besten auf sogenannten Quanten-Computern implementiert, die Qubits und die Qubit-Algorithmen. Solange man sich also mit den Objekten nur algorithmisch beschäftigt, spielen Quanten im physikalischen Sinne keine Rolle. So auch in unserer Blog-Serie. Zugegeben, die Bezeichnung Qubit ist natürlich eine Zusammenfügung aus Quantum und Bit.
Quanten dagegen sind ein physikalisches Konzept. Wen das nicht interessiert, kann diesen Absatz ab hier überspringen. Man kann auch ohne dieses Wissen alles Weitere verstehen, da sind wir sicher.
Ein Quant bezeichnet ursprünglich die kleinste Einheit einer physikalischen Wirkung (Wikipedia: Plancksches Wirkungsquant). Max Planck erkannte, dass in der physikalischen Welt alle Veränderungen in "Sprüngen" von mindestens Quantengröße vor sich gehen - wenn man genau genug hinschaut. (Der viel zitierte "Quantensprung" ist also eigentlich die kleinste Veränderung, die man erwirken kann.)
Im atomaren und sub-atomaren Bereich der Physik gibt es vielfältige Abläufe, die in diesem Sinne "gequantelt" von statten gehen. Wenn zum Beispiel ein Elektron auf ein niedrigeres Energieniveau zurück fällt, gibt es Energie von der Größe eines Vielfachen des Planckschen Quants ab und das in Form eines Lichtteilchens (Photon). Üblicherweise werden daher auch diese "Energiepakete" als (Licht-)Quanten bezeichnet. Typisch für ein Photon ist, dass es je nach experimenteller Bedingung ein - im Sinne makroskopischer Phänomene - teilchenartiges oder ein wellenartiges Verhalten zeigt. Auch andere physikalische Objekte, wie z.B. ein Elektron, kann dieses Verhalten zeigen, weshalb man sie ebenfalls als physikalische Quantenobjekte oder -systeme auffasst bzw. verwendet.
Das Verhalten von Quantenobjekten lässt sich durch eine (mathematische) Zustandsbeschreibung charakterisieren (Quantenzustand), etwa durch mathematisch anspruchsvolle partielle Differentialgleichungen (z.B. die Schrödinger-Gleichung). Damit lassen sich bestimmte Quanteneigenschaften erklären und durch einen Mess-Prozess bestimmen.
Grundlage für allgemeine Quanten-Computer, auf denen wir Qubit-Algorithmen ablaufen lassen können, sind Quantensysteme, also physikalische Systeme, bei denen sich Zustandsänderungen mittels Quanten vollziehen. Für die Realisierung von Qubits verwendet man Systeme mit Quanteneigenschaften, die grundsätzlich zwei gegensätzliche Ausprägungen haben, und deren allgemeiner Zustand als Überlagerung dieser beiden Ausprägungen dargestellt werden kann (Superposition genannt).
Eine weitere Besonderheit, die wir auch bei den Qubit-Algorithmen verwenden, ist, dass man den Quantenzustand eines Systems nicht wissen kann - prinzipiell nicht! Was man tun kann, ist, ein Quantensystem messen und aus den Messergebnissen gewisse Rückschlüsse auf den Zustand ziehen. Quantenphysiker können aber durchaus Quantenzustände "herstellen", durch physikalische Operationen und durch Überprüfung mit Messungen. Allerdings kann man ein Quantensystem nicht zweimal messen; nach dem ersten Messen ist es nicht mehr in dem Zustand, in dem es bei der Messung war. Schlimmer noch, bei den meisten Messungen am irgendwie "gleich hergestellten" Quantenzustand bekommt man unterschiedliche Ergebnisse! Wenn die Messung aber vielfach wiederholt wird, kann man allerdings eine Häufigkeitsverteilung der Ergebnisse erstellen und daraus so etwas wie die Wahrscheinlichkeit für die einzelnen Ergebnisse ableiten. Der Quantenzustand "äußert" sich dann per Messungen in Form einer Wahrscheinlichkeitsverteilung für die möglichen Ergebnisse. Höchst eigenartig - aber darauf basiert letztlich das Besondere an Qubits und Qubit-Algorithmen - sie sind eine Abstraktion des Geschehens bei bestimmten physikalischen Quantensystemen. Und darauf wollen wir uns hier beschränken.
Ein faszinierendes und auch für den Physik-Laien gut verständliches Video findet man hier. Es demonstriert physikalisch die auch in der Qubit-Algorithmik wichtigen Begriffe Superposition und Verschränkung sehr anschaulich anhand von Photonen-Experimenten.
Hier endet der "Quanten-Absatz".
Qubit Prinzipien
Das Ungewöhnliche an Qubits lässt sich durch zwei, drei Grundprinzipien beschreiben:
Erstens, ein Qubit, oder auch ein Qubit-System, hat Zustände, die sich nicht direkt zeigen, sondern nur indirekt, wenn man sie misst. Dabei kann es durchaus sein, dass verschiedene Zustände gleiche Messergebnisse liefern.
Zweitens, es gibt Zustände, deren Messung nicht ein eindeutiges Ergebnis liefern - wie 0 oder 1 beim "Messen" normaler Bits (z.B. Lesen, Ausdrucken, Verrechnen). Ihr Messergebnis kann nur durch feste Wahrscheinlichkeiten für verschiedene mögliche Ereignisse (z.B. 0 oder 1) charakterisiert werden. Das ist eine Besonderheit, die wir am besten durch eine einfache Analogie verdeutlichen.
Man stelle sich vor: In einem Pausenraum stehen zwei Getränkeautomaten. Der eine Automat ist ein Becher-Automat. D.h. wenn man C oder L drückt und Geld einwirft, fällt ein Becher und wird mit Cola, bzw. Limo gefüllt. Außerdem gibt es die Taste H (für Halbe-Halbe), damit bekommt man eine Mischung halb Cola, halb Limo, also so etwas wie Mezzomix. Insgesamt also: drei Tasten, drei Getränke. Der andere Automat gibt nur Getränke in Flaschen aus. C und Geldeinwurf: eine Flasche Cola, bei L eine Flasche Limo. Und jetzt kommt's: Was, wenn man H wählt? Nicht etwa eine Flasche Mezzomix, sondern Cola! Beim nächsten Mal: wieder Cola. Also sind C und H einfach zwei Tasten für Cola? Beim nächsten Mal H gibt es eine Limo. Der nächste bekommt wieder eine Cola, die nächsten Schüler Limo, Limo, Cola usw. jeweils ein Flasche. Also drei Tasten, zwei "Outputs"? Die Schüler finden das krass und kaufen nur noch H - wegen des Überraschungseffekts. Ein Schüler kommt auf die Idee zu zählen. Über die ganze Pause hinweg zählt er 14 mal Cola und 16 mal Limo. Aha, das ist es also, was H bedeutet: Cola und Limo-Flaschen werden (zufällig) in etwa der Hälfte aller Käufe ausgegeben.
Der zweite Automat ist ein "Qubit-Cola-Limo-Automat": Mit Taste C gibt's Cola, mit L gibt's Limo und mit H gibt's ... wir haben's gesehen.
Drittens, und dann reicht es erst einmal, man kann alle diese Zustände "herstellen". D.h. es gibt Qubit-Operationen (ähnlich wie Bit-Operationen), die einen Zustand in einen nächsten überführen. Und mit solchen kann man alle Qubit-Zustände erreichen, sogar determiniert.
Aus Qubits und solchen Operationen werden Qubit-Algorithmen aufgebaut - die Messungen nicht zu vergessen.
Spannend! Mit Qubit-Algorithmen auf echten Quantenrechnern experimentieren
Seit etwa 2017 gibt es von IBM die in der Cloud verfügbare Umgebung IBM Q Experience. Sie umfasst den Zugang zu realen Quanten-Computern, QC-Simulatoren und Programmierumgebungen. Besonders motivierend ist die Möglichkeit, kleine Qubit Algorithmen grafisch zu erstellen (mit dem Circuit Composer). Für fortgeschrittene Qubit-Algorithmen bietet sich ein mit Python verwendbares Paket für Qubit-Programmierung an (das Qiskit). In dieser Blog-Serie beschränken wir uns auf den IBM Q Composer zur Illustration und beim Experimentieren mit Qubit-Algorithmen. Programmieren ist keine Voraussetzung für diese Q-Serie. Wer aber Spaß daran hat, kann viele interessante Dinge mit dem Composer oder in der Kombination von Python und Qiskit ausprobieren - ebenfalls direkt in der IBM Q Experience Cloud (via Browser). *)
Auch Google hat eine sehr leistungsfähige QC-Umgebung in der Cloud verfügbar gemacht (Google Cirq). Sie bietet ähnliche Möglichkeiten zur Qubit-Programmierung wie die IBM Umgebung und kann hier als Alternative zur IBM Q Experience durchaus in Betracht gezogen werden. Microsoft bietet mit Azure Quantum eine Entwicklungsplattform mit der Programmierumgebung QDK (Quantum Developer Kit) und Simulatoren. Die Quantum-Hardware wird über Azure von Partnern integriert.
Es folgt eine Übersicht über die einzelnen Abschnitte der Q-Serie, nummeriert von Q1 bis Q16.
Qubit-Algorithmen für die Schule - die Q-Serie
Q1 Etwas ist anders! - Qubit-Algorithmen
Die An-Moderation.
Q2 Etwas ist anders! - Hello Qubit World
Wir machen uns damit vertraut, wie ein Qubit-Algorithmus "aussieht", auch wenn wir die Details jetzt noch nicht verstehen. Jedenfalls schon ganz schön exotisch.
Q3 Vom Bit- zum Qubit-Modell
Wir entdecken das Bit neu als "kleinen Bruder" des Qubits. Wir finden eine Black Box mit der Bezeichnung BIT vor, experimentieren damit und machen uns so ein BIT-Modell. Am Ende finden wir eine Blue Box mit der Aufschrift ZBIT vor.
Q4 ZBIT – unterwegs zum Qubit-Modell
Wir experimentieren mit der ZBIT-Box und stellen fest, dass sie sich an einer Stelle ganz anders verhält als die BIT-Box, nämlich zufällig! Damit sind wir schon auf dem halben Weg zum Qubit. Wir untersuchen die Blue Box und machen uns ein Modell, das wie eine ZBIT-Box funktionieren soll. Stellen allerdings fest, dass das im ersten Anlauf nicht richtig klappt.
Q5 Ein verbessertes ZBIT-Modell
Wir entwickeln ein Modell für ZBIT, das passt. D.h. man kann die Experimente damit nachvollziehen und erklären. Und Voraussagen machen, die wir durch Experimente mit der Blue Box bestätigen können. Bis hierhin haben wir auch schon einiges an abkürzenden Schreibweisen verwendet, die später auch als Gerüst für die Beschreibung von Qubit-Algorithmen dienen. Wir haben auch gelernt, dass "Messen" eine wichtige Rolle spielt, um Aussagen über den Zustand eines ZBIT-Modells zu machen.
Q6 Zwischenspiel - ZBIT-Spielereien
Namen sind Schall und Rauch. Nicht wie sie heißen, macht Zustände zu ZBIT-Zuständen, sondern wie man sie verwendet. Wir spielen ein wenig herum mit verschiedenen Möglichkeiten ein ZBIT-Modell zu beschreiben: vom Basketball-Spiel über die Grafik aus Q2 (Hello Qubit-World) bis zu Punkten im x-y-Koordinatensystem.
Q7 Qubit - Ein Modell für Qubit Algorithmen
Mit der Grey Box QBIT lernen wir das Verhalten von Qubits kennen und verstehen. Die "Experimente" sind vielfältiger, damit auch ihre Beschreibung als elementare Algorithmen. Die QBIT-Zustände haben wir aber schon am Ende der ZBIT-Spielereien richtig als Punkte im x-y-Koordinatensystem dargestellt. Das ZBIT ist tatsächlich schon ein vereinfachtes Qubit - mit seinen Zuständen, Operatoren und Messvorschriften.
Q8 Fingerübungen - Einfache Qubit Algorithmen ausprobiert
Einfache 1-Qubit und erste 2-Qubit Operationen werden vorgestellt in Form einer einfachen symbolischen Notation und als Gates (Gatter) in Composer Circuits (Schaltkreise). Wir lernen die Wirkung und das Zusammenwirken von einigen Gates verstehen, darunter ein erstes Controlled Gate, CNOT, dessen Wirkung auf einen Qubit-Zustand vom Zustand eines anderen Qubit abhängt. Gelegentlich verwenden wir alternativ zur Koordinatendarstellung auch die |0>, |1> Form (Ket-Notation) zur Kennzeichnung von Zuständen.
Q9 Verschränkung und andere 2-Qubit Phänomene
Wir probieren weitere einfache 2-Qubit Algorithmen aus und erklären die Zustandsabfolge und die Messergebnisse. Wir stoßen dabei erstmalig auf die Verschränkung von 2-Qubit-Zuständen und den Kickback-Effekt, beides wichtige Elemente in Qubit-Anwendungen. Die Wirkung von Gates und die Zustandsabfolgen werden berechenbar durch einfache Formeln auf Basis der Zustandskoordinaten.
Q10 Qubit-Algorithmen - Hinter die Kulissen geschaut
"Hinter die Kulissen schauen" heißt, die Effekte der Zwei- und Mehr-Qubit Algorithmen durch Zustandsübergänge und Messungen zu erklären. Mittels Koordinatendarstellung und Gate-Formeln. Bei dieser Gelegenheit lernen wir noch einige weitere Gates aus dem Repertoir der Qubit-Algorithmik und des Composers kennen. Unter anderem das über 3 Qubits wirksame Toffoli Gate.
Q11 3-Qubit Circus
Mit mehr Qubits werden Qubit-Algorithmen vielfältiger - aber auch komplizierter zu verfolgen. Wir konstruieren und analysieren einige 3-Qubit Circuits. Auch bei 3-Qubit-Systemen gibt es den Effekt der Verschränkung, sogar noch vielfältiger.
Q12 Ein echter Quanten-Würfel in 3 Qubits
Mit diesem Abschnitt und den folgenden stellen wir Qubit-Algorithmen vor, die man (fast) als praktische Anwendungen sehen kann. Der erste ist ein normaler 6-flächiger Würfel, der, wenn er auf einem realen Quantencomputer ausgeführt wird, einen echten Zufallswürfel darstellt, der nach den Gesetzen der Quantenphysik prinzipiell nicht vorausberechenbar ist. Hilfestellung für die Idee dieses 3-Qubit Algorithmus liefert eine 3-Qubit-Verschränkung, der sog. W-Zustand, den wir hier näher untersuchen.
Q13 Superdichte Codierung und Quanten-Kommunikation
Wir konstruieren und untersuchen Qubit-Algorithmen, mit denen man prinzipiell mehr Bits in weniger Qubits codieren und übertragen kann. Also z.B. 2 Bits in einem Qubit. Das Modell der superdichten Quanten-Kommunikation ist zwar ungewöhnlich aber mit unseren Mitteln leicht nachvollziehbar. Auch hier spielt wieder die Verschränkung eine Rolle. Das Verfahren funktioniert auch in Realität. Quanten-Kommunikation hat man schon über hunderte von Kilometern getestet,
Q14 Quanten-Teleportation
Während Quanten-Kommunikation die Übertragung von Bits mittels verschränkter Qubits ermöglicht, bedeutet Quanten-Teleportation (trotz dieses SciFi Wortes) das Übertragen eines Qubit-Zustands auf ein anderes, entferntes Qubit mittels Bit-Information, die zuvor aus Messungen gewonnen wurde. Wir konstruieren, anlaysieren und diskutieren den Quanten-Teleportations-Algorithmus.
Q15 Ein Geheimnis mit einer Frage rauskriegen - Bernstein-Vazirani-Algorithmus
Wir stehen vor der Aufgabe, eine geheime Bit-Kette herauszufinden, etwa einen Code oder den Weg durch ein Labyrinth. Wir probieren es mit klassischen (Bit-)Algorithmen, die typischerweise immer eine gewisse Anzahl von "Fragen" benötigen, und schließlich mit einem Qubit-Algorithmus, der das mit nur einer "Frage" schafft. Wir haben damit ein erstes Beispiel für einen Beschleunigungseffekt durch Qubit-Parallelismus. Wir untersuchen, wie das geht und warum das geht und wie man das allgemein verwenden kann.
In diesem Abschnitt führen wir auch die Qubit-Programmierung mittels Qiskit ein. Ein Link verweist auf ein vollständiges, lesbares Qiskit/Python-Programm.
Q16 Was man so liest
Hier diskutieren wir den Sprachgebrauch und einige typische Aussagen, wie sie in den Medien zum Thema Quantencomputing immer wieder auftauchen. Was ist gemeint, was ist dran, wie muss man das verstehen und - was steckt eigentlich dahinter? Wir tun dies auf der Basis des erworbenen Verständnisses aus dieser Q-Serie.
QX Etwas ist anders - und es gibt noch viel mehr
Es ist zu erwarten, dass sich weitere interessante Ideen und Algorithmen ergeben, die sich auf der Ebene "Schulwissen" ebensogut darstellen lassen, wie die bisherigen Beispiele, auch wenn sie vielleicht noch etwas komplizierter werden. Nur was man erklären kann, hat man verstanden. Ideen können gerne auch aus Kommentaren und Mitteilungen zu dieser Blog-Serie kommen. Die würden wir in weiteren Blog-Abschnitten unter QX aufnehmen.
Und hier beginnt die Q-Serie.
*) Update Aug. 2020: Das Erscheinungsbild der IBM Quantum Experience Umgebung hat seit etwa August 2020 ein Update erfahren. Insbesondere das User Interface des Circuit Composers hat sich etwas verändert. Es gibt mehr vordefinierte Gates, ein paar andere Voreinstellungen und Farben. Mit Blick auf die Beispiel-Circuits in der Blog-Serie haben sich aber im Wesentlichen nur die Farben der Gates geändert. Interessant ist auch, dass auf der Oberfläche nicht nur der Circuit dargestellt wird, sondern auch gleich die Ergebnisse von Messungen, sowie andere interessante Informationen, auf die wir in den Blogs nicht eingegangen sind. Dazu gehört auch, wenn man es richtig versteht, eine Darstellung der aktuellen Zustandssuperposition (Statevector), also die n-Qubit Basiszutände mit ihren Koeffizienten (Amplituden genannt).
Dank
Unser Dank geht unter anderem an Dr. Roman Wienands für die Antworten auf viele algorithmische Detailfragen. Dr. Wienands und der Zweitautor führen übrigens seit vielen Jahren sehr erfolgreich Seminare zu "Algorithmen im Schulunterricht" für die Lehrerausbildung am Mathematischen Institut der Universität zu Köln durch. Seit einiger Zeit auch zu Themen aus der Künstlichen Intelligenz und dem Quantencomputing.
Der Zweitautor hat darüber hinaus die Kapitel der Q-Serie als Diskussionspartner intensiv begleitet, die Texte akribisch durchgesehen und, natürlich, viele Fehler und einige Unverständlichkeiten gefunden.
Zu diesem Einführungstext wird es ein Companion-Text geben, der die gesellschaftlichen und bildungspolitischen Aspekte des Quanten-Computing sowie dessen erwartete Möglichkeiten beleuchtet.
Kontakte
Prof. Dr. Ulrich Trottenberg: ulrich.trottenberg@interscience.de
Dr. Bernhard Thomas: bernhard.thomas@interscience.de
