Q16 Quanten und Qubits - Was man so liest
Von Bernhard Thomas und Ulrich Trottenberg
Quanten-Computing wird in den Medien, aber auch in Vorträgen und in der Fachliteratur mit einer Reihe von Aussagen charakterisiert, die als Sprachkonstrukte ziemlich exotisch klingen - nach einer anderen Welt, in der logisch Unmögliches möglich scheint. Wir wollen uns einige dieser Sprachfiguren ansehen und überlegen, was dahinter steckt.
Unsere bisherigen Blog-Abschnitte über Qubit-Algorithmen sollten ausreichen, hier ein klares Verständnis zu schaffen. Hier die Übersicht über die Aussagen.
"Quanten können 0 und 1 gleichzeitig sein"
"Mit n Qubits kann man 2**n Zahlen gleichzeitig darstellen"
"Für N Zahlen benötigt ein Quanten-Computer nur log(N) Qubits"
"Ein Quanten-Computer kann mehrere Berechnungen gleichzeitig durchführen (Quanten-Parallelismus)"
"Was auf herkömmlichen Rechner Jahre dauert, kann ein Quanten-Rechner in Sekunden erledigen (Exponentielle Beschleunigung)"
"Quanten-Rechner werden herkömmlichen Rechnern überlegen sein (Quanten-Supremacy)"
"Jedes zusätzlich Qubit verdoppelt die Leistungsfähigkeit des Systems"
"Quanten können 0 und 1 gleichzeitig sein"
Dieser Satz und Abwandlungen davon ziehen sich durch die Quanten-Computing-Literatur wie ein Mantra des QC. Auch wenn er gelegentlich nur als Metapher gesehen wird, suggeriert dieser Satz in der öffentlichen Diskussion eine mystische Eigenschaft der Quanten, nicht zuletzt illustriert durch das Bild von Schrödingers Katze, die "gleichzeitig tot und lebendig" ist.
Damit werden auch die informatischen Gegenstücke der Bits, die Qubits, charakterisiert. Im Gegensatz zu Bits, die nur "0 oder 1" sein können, können Qubits "0 und 1 gleichzeitig" sein.
Wie könnten wir das feststellen? Wir wissen, dass die Messung eines Qubits entweder 0 oder 1 ergeben kann, aber nicht beides. Wenn wir mehrfach messen, bekommen wir manchmal eine 0, manchmal eine 1 als Ergebnis, aber nie "gleichzeitig". Was kann also gemeint sein - wenn es überhaupt einen Sinn ergibt.
Es gibt Varianten dieser "Gleichzeitig"-Sprachfigur, die etwas tiefergehend klingen: "Quanten können verschiedene Zustände gleichzeitig einnehmen". Wir wissen, dass man Zustände von Systemen in Form von mathematisch eindeutigen Ausdrücken beschreiben kann - so auch Qubits und Qubit-Systeme. Ausgehend von einem Anfangszustand sahen wir, wie mittels Qubit-Operationen (oder Gates) ein Qubit-Zustand in einen nächsten überführt werden kann. Zu jedem Zeitpunkt ist der Zustand des Qubits daher eindeutig festgelegt. Wenn wir nicht unsere normale zweiwertige Logik (2 Wahrheitswerte: wahr, falsch - oder 0, 1) in Frage stellen, kann ein Qubit nicht zwei verschiedene Zustände gleichzeitig haben. Eine Zahl, ein mathematischer Ausdruck, der einben Zustand beschreibt, kann nicht gleichzeitig 0 und 1 sein: z = 0 = 1?
Manchmal findet man Texte, in denen das "Gleichzeitige" durch die "Superpostion" ergänzt wird: "Quanten können in einer Superosition von 0 und 1 gleichzeitig sein". Wir wissen, was eine Superpostion ist. Z.B. ist 1/√2 (|0>+|1>), die Hadamard-Operation auf den Basiszustand |0>, eine Superpostion (oder mathematisch: Linearkombination) der Qubit-Zustände |0> und |1>. Wir haben Qubit-Zustände meist in Form von x-y-Koordinaten eines Punktes auf dem Einheitskreis beschrieben - im Beispiel also (1/√2,1/√2). Somit können wir korrekt formulieren: Ein Qubitzustand hat zwei Koordinaten. Aber was heißt dann "gleichzeitig"? Wenn jemand in Ingolstadt ist, befindet er sich z.B. auf der Strecke von München nach Nürnberg - aber ist er (möglicherweise) in München und Nürnberg "gleichzeitig"?
Wenn auch die Redewendung "... kann 0 und 1 gleichzeitig sein" etwas Unsinniges suggeriert, können wir sie als solche akzeptieren, wenn man sie auf die Möglichkeit einer Superposition von zwei (Basis-)Zuständen eines Qubits zurückführt. Darin unterscheiden sich Qubits und Bits tatsächlich.
Und während ein Bit nur einen der beiden Zustände 0 oder 1 repräsentieren kann (siehe BIT-Box in Q3), kann ein Qubit einen Zustand aus einer unendlichen Menge von Superpositionszuständen annehmen. Wobei wir das "unendlich" im Sinne aller Punkte auf dem Einheitskreis verstehen, ohne zu fragen, ob wirklich unendlich viele Superpositionen realisierbar sind (technisch und quantenmechanisch).
Eine elegante und gleichzeitig korrekte, einfache Erklärung finden wir im Glossar der IBM (Übersetzung DeepL):
Ein Qubit (ausgesprochen "kju-bit" und kurz für Quantenbit) ist der physikalische Träger der Quanteninformation. Es ist die Quantenversion eines Bits, und sein Quantenzustand kann Werte von |0> , |1> oder die Linearkombination von beiden annehmen, was ein Phänomen ist, das als Superposition bekannt ist.
Mehr ist eigentlich nicht zu sagen.
"Mit n Qubits kann man 2**n Zahlen gleichzeitig darstellen"
Mit n Bits kann man zwar auch 2**n verschiedene Zahlen darstellen - gemeint sind Binärzahlen in Form von Bitketten - aber immer nur eine zu einem Zeitpunkt, z.B. im Speicher eines klassischen Computers.
Diese Aussage zusammen mit dem "Quantenparallelismus" (s.u.) soll die überragende Leistungsfähigkeit von Quanten-Computern deutlich machen. Man liest auch: "Mit jedem weiteren Qubit verdoppelt sich die Kapazität" und "Schon 300 Qubits können mehr Werte speichern, als das bekannte Universum Teilchen enthält".
Nun ja, wie soll man das verstehen? Zunächst zu den beiden letzten Versionen des "Kapazitätssatzes": Auch mit jedem weiteren Bit verdoppeln sich die möglichen Werte, die man speichern - und wieder lesen - kann. Immer einer zu einer Zeit (Schreib-Lese-Zyklus). Und mit 300 Bits kann man mehr als alle Teilchen des bekannten Universums abzählen, oder je eine Zahl zu einem Zeitpunkt im Bereich 0 bis 2**300-1 speichern. Bei Qubits liegt das Geheimnis offenbar wieder im "gleichzeitig". Wieder nur eine Metapher?
Ein System von n Qubits, z.B. n=3, befindet sich zu einem Zeitpunkt in einem Zustand (von prinzipiell unendlich vielen), der eine Linearkombination (Superposition) von nunmehr 2**n Basiszuständen ist, also 8 bei n=3. In der ket-Schreibweise tritt jede n-lange Bitkette als ein Basiszustand auf, bei n=3 also |000>, |001>, |010>, |011>, |100>, |101>, |110>, |111>. Bei n = 300 sind es halt ......
Denken wir an Koordinatensysteme, wie z.B. in Q11, dann haben wir ein 8-dimensionales Koordinatensystem und jeder 3-Qubit-Zustand wird durch 8 Koordinaten beschrieben. "Gleichzeitig" - für einen Punkt braucht man 8 Koordinaten "gleichzeitig".
Kann man in einer Superposition von 2**n Basiszuständen das gleichzeitige Speichern von 2**n Zahlen sehen? Nehmen wir eine gleichmäßige (uniforme) Superposition, d.h. alle Basiszustände kommen mit dem gleichen Koeffizienten vor. Bei n=3 also mit 1/√8.
Speichern nützt nur dann etwas, wenn man mit dem Gespeicherten etwas anfangen kann, z.B. weiter verarbeiten mittels Qubit-Operationen oder Lesen, d.h. Messen. Beim Weiterverabeiten zu einem neuen Zustand können tatsächlich alle Komponenten der Linearkombination in einer Operation berücksichtigt werden (Quantenparallelismus, s.u.). Beim Messen (gegen die Basiszustände) erhält man eine Häufigkeitsverteilung über alle Bitketten, die als Basiszustände in der aktuellen Superposition vertreten sind. Sind einige nicht vertreten, tauschen sie, bis auf Quantenfehler, auch nicht im Messergebnis auf.
Aber was machen wir damit? Welche Information ziehen wir daraus? Dass 2**n Bitketten beim Messen auftreten können, wussten wir schon vorher. Wir "lesen" also nichts Neues. Wenn wir 2**300 Teilchen mit unterschiedlichen Bitketten versehen wollten, konnten wir das auch schon ohne Quanten-Computer (QC).
Wo liegt also die Information, die wir durch die Quanten-Berechnung gewonnen haben? Wohl in der gemessenen Häufigkeitsverteilung:
- Wir schauen nur auf "vorhanden" und "nicht vorhanden" von gemessenen Bitketten. Eine häufige Form der Interpretation von QC-Ergebnissen, z.B. beim Herausfinden eines Orakels, wie im Bernstein-Vazirani Problem oder dem von Deutsch-Josza. Man kann sich das so vorstellen: Der Qubit-Algorithmus "rechnet" mit den 2**n Basiszuständen des n-Qubit Systems, der Ergebnis-Zustand enthält aber in nur einen Basiszustand, der dann bei der Messung eine ziemlich eindeutige Bitkette liefert. Eine solche Methode ist auch die sogenannte Amplituden-Verstärkung (amplitude amplification). Zum Auffinden einer bestimmten Bitkette beginnt man mit einer uniformen Superposition und verändert diesen Zustand Schritt für Schritt so, dass die Amplitude des Basiszustands mit der gesuchten Bitkette zunehmend "größer" wird. Die Iteration wird beendet, wenn man nahe genug an der gesuchten Bitkette ist, d.h. wenn beim Messen diese Bitkette eine überragende Wahrscheinlichkeit erreicht. Das Verfahren wird auch Grover-Iteration genannt.
- Uns interessiert ein "numerisches" Ergebnis, z.B. eine Zahl oder eine Reihe von Zahlen (Vektor), die sich bei der Messung am Ende der Rechnung als Häufigkeiten bestimmter Bitketten ergeben. Als "numerisches" Ergebnis nimmt man dann die Liste dieser Häufigkeiten. Hier stoßen wir aber auf verschiedene Probleme. Eines davon ist, dass ein echter QC die Häufigkeiten nicht exakt misst. Um halbwegs brauchbare Werte abzuleiten, müssen wir das QC Programm wiederholt durchlaufen lassen. Wie oft? Für n=3 kann man das ja einmal ausprobieren mit dem IBM QC. Wie oft bei n=50 oder n=300?
"Für N Zahlen benötigt ein Quanten-Computer nur log(N) Qubits"
Dies ist eine Variante der vorigen Aussage und besagt: "Während man auf herkömmlichen Computern für N Zahlen auch N Speicherplätze benötigt, braucht ein Quanten-Computer nur log(N) Qubits". Man hat also, umgekehrt gesehen, einen exponentiellen Effekt. Und damit ist ein Quanten-Computer exponentiell leistungsfähiger als ein herkömmlicher. Wie auch immer das gemeint ist, es läuft darauf hinaus, dass man eine Überlagerung der N Basiszustände eines "log(N) großen" Qubit-Systems herstellt, bei der die Koeffizienten (auch Amplituden genannt) gerade die gewünschten N Zahlen sind. Wenn man also weiß, wie, kann man einen solchen Superpositionszustand als "Input" herstellen, und einen Qubit-Algorithmus damit weiterrechnen lassen. Das ist das sog. Amplituden-Verfahren oder auch Amplituden Encoding.
Aber halt! Die N Amplituden müssen ja in der Summe der Quadrate 1 ergeben. Schränkt das nicht die freie Wählbarkeit der N Zahlen ein? Nicht wirklich - man muss nur vorher jede Zahl durch die Summe aller Quadrate teilen, genauer, durch die Quadratwurzel dieser Summe. Damit kann man dann "Quanten-Rechnen". Allerdings tritt bei der Ergebnis-Festellung wieder das Problem aus 2. auf.
Um die N Zahlen als Input verwenden zu können, muss man zu Beginn des Qubit-Algorithmus geeignete Qubit-Operationen (Gates) ausführen, so dass sie in einer Superposition zu Koeffizienten von Basiszuständen werden. Das kann trotz "Quantenparallelität" aufwendig sein. Hier ein Beispiel:
Angenommen, wir wollen die 4 Zahlen 1.0, 1.0, √2 = 1.414, 2.0 als Input in Form von Amplituden für ein 2-Qubit-System bereitstellen (N=4, n=2). Die Summe der Quandrate ist 1.0+1.0+2.0+4.0 = 8.0. Die Wurzel daraus ist √8. Dadurch müssen wir die 4 Zahlen teilen, damit diese eine gültige 2-Qubit Superposition ermöglichen: 1/√8, 1/√8, 1/√4, 1/√2. Es ist damit z.B. der Zustand 1/√8 |00> + 1/√8 |01> + 1/√4 |10> + 1/√2 |11> durch einen Qubit-Circuit herstellbar. Wie geht das? Hier ist eine Lösung:
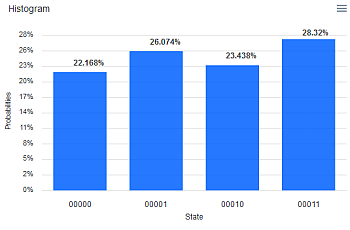
Das "Fine-Tuning" der Amplituden erfolgt hier mittels Drehungen (Ry). Der resultierende Zustand ist verschränkt, d.h. er kann nicht als Kombination der einzelnen Qubits hergestellt werden. Das kann man nach der Methode in Q9 nachprüfen. (Ergebnis eines Simulatorlaufs mit 1024 shots.)
"Ein Quanten-Computer kann mehrere Berechnungen gleichzeitig durchführen"
Diese Aussage wird häufig als Verdeutlichung des sog. Quanten-Parallelismus verwendet. Auch hier wird wieder das Mantra-Wort "gleichzeitig" verwendet, dieses Mal aber in einer sinnvollen Bedeutung, nämlich im Gegensatz zu "nacheinander" (sequentiell). Natürlich können auch herkömmliche Computer heutzutage mehrere Berechnungen zeitlich parallel ausführen. Der Unterschied ist aber technisch fundamental: Herkömmliche Parallelrechner (z.B. MIMD-Architekturen) führen mehrere, durchaus auch verschiedene, Computerbefehle (Instructions) zur gleichen Zeit aus und verwenden dabei u.U. unterschiedliche Daten als Input.
Quanten-Computer führen zu einem Zeitpunkt einen Befehl (in Form von Gates) auf einer Datenstruktur aus. Die Datenstruktur ist der aktuelle Zustand eines n-Qubit-Systems, also meist eine Superposition oder gar eine Verschränkung. Der Zustand eines n-Qubit-Systems kann aber, wie wir zuvor gesehen haben, bis zu N=2**n Zahlen (in Form von Amplituden) repräsentieren. Indem der Qubit-Befehl auf den Zustand wirkt, wirkt er simultan auf alle Basiszustände, die in der Superposition vorkommen. Als Ergebnis können sich damit simultan alle Amplituden der Basiszustände verändern. Bingo!
Mathematisch gesehen ist das überhaupt nichts Ungewöhnliches. Eine Matrix A "wirkt" bei Multiplikation mit einem Vektor x auf alle seine Komponenten "gleichzeitig": y= Ax (Lineare Algebra). Wird ein Punkt (x,y) mittels einer Funktion F verschoben, dann werden alle Koordinaten "gleichzeitig" verschoben: (u,v) = F(x.y). Und auch die Qubit-Operatoren (Gates) können mathematisch als Matrizen dargestellt und verwendet werden. Wenn es allerdings ans praktische Rechnen geht, etwa mit einem Algorithmus, der die Matrixmultiplikation explizit durchführt, dann geht es klassisch (auf einem herkömmlichen Rechner) wieder nur Schritt für Schritt: die Operation wird in viele Einzelschritte zerlegt, die nacheinander ausgeführt werden. Hier unterscheiden sich klassische und Quanten-Computer tatsächlich fundamental. Quanten-Computer, wie die von IBM, sind technisch so aufgebaut, dass sie eine komplette Superposition in einem, statt in vielen Schritten verarbeiten können.
Wie man sich das vorstellen kann, zeigen wir an einem einfachen Beispiel: Das exklusive Oder (XOR) von zwei Bits entspricht der einfachen Bit-Addition bis auf die Operation "1+1", die 0 ergibt statt 2. (Dafür verwendet man auch das Symbol ⊕ statt +). Wir können die Bit-weise XOR-Berechnung auch als Qubit-Circuit durchführen. Das ergibt die 4 Auswertungen in der Abbildung, wobei jeweils q0 und q1 auf Zustand 0 bzw. 1 gesetzt werden und das Ergebnis den neuen Zustand von q1 ergibt.
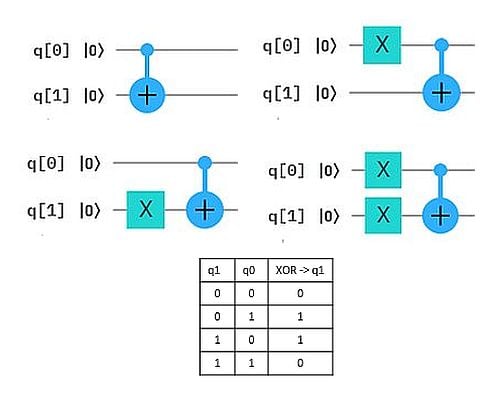
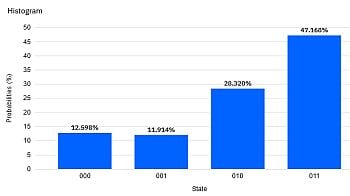
Quanten-Parallelismus ermöglicht aber Superpositionen statt einzelner Basiszustände als Input zu präparieren, typischerweise mit dem H-Gate (Hadamard-Gate). Damit muss die Berechnung nur einmal ausgeführt werden und wir erhalten alle 4 Ergebnisse auf einmal.
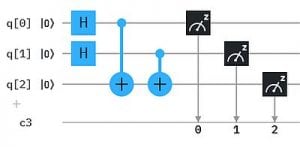
Um die Ergebnisse einfacher "lesen" zu können, haben wir hier das XOR Ergebnis auf ein drittes Qubit q2 übertragen. So erhalten wir als Messergebnis genau die obige XOR Tabelle mit XOR -> q2 : 000, 101, 110, 011 (q2 steht hier wieder jeweils ganz links in der Bitkette).
"Was auf herkömmlichen Rechnern Jahre dauert, kann ein Quanten-Rechner in Sekunden erledigen"
Als Begründung liest man dabei oft, dass Quantenrechner "exponentiell schneller" rechnen können als herkommliche. Was bedeutet das?
Das heißt zum Beispiel folgendes: Wenn wenn wir zwei Methoden haben, die eine Aufgabe lösen, etwa eine Berechnung durchführen oder ein "Geheimnis" (Q15) zu finden, und die eine Methode benötigt N Zeiteinheiten oder Rechenschritte, die andere aber nur log(N) viele, dann stellt die zweite Methode eine exponentielle Verbesserung - oder Beschleunigung - gegenüber der ersten dar. (Denn, für k=log(N) ist N=exp(k).)
Es gibt eine ganze Reihe von solchen "Beschleunigungsbeziehungen" zwischen Methoden zur Lösung gleicher Aufgaben. Der Grover Qubit-Algorithmus benötigt nur etwa √N Schritte gegenüber N Schritten bei der klassischen Methode. Hier haben wir also eine quadratische Beschleunigung. In Q15 hatten wir das am Beispiel des Bernstein-Vazirani-Algorithmus diskutiert.
Solche Beschleunigungen gibt es von je her auch im klassischen Computing als Effekt einer algorithmischen Verbesserung. So gibt es z.B. unterschiedliche Sortier-Algorithmen, die sich bezüglich ihres Rechenaufwands erheblich unterscheiden, oder auch Verfahren zur numerischen Simulation, bei denen sogenannte Mehrgitterverfahren große Beschleunigungsraten bringen.
Der tatsächliche Beschleunigungseffekt des Quanten-Computing gegenüber herkömmlichen Bit-Computing beruht auf einer Kombination von zwei Dingen: dem Quanten-Parallelismus der Hardware (s. voriger Abschnitt) und dem Algorithmus, der für Qubits konstruiert werden kann.
Ein Rechenbeispiel: Hätte man eine (hypothetische) Aufgabe, die auf einem gewöhnlichen Rechner mit dem schnellsten Algorithmus 10 Jahre dauern würde, dann würde eine exponentielle Beschleunigung auf einen Zeitaufwand von rund 20 Sekunden führen: log(10*360*24*60*60) = log(311040000) = 19,56. Diese Zahlen sind allerdings eher fiktiv, da wie keine konkrete Aufgabe vor Augen haben und Wiederholungen und anderen "Overhead" nicht berücksichtigen. Aber es zeigt, wie sich die Größenordnung ändern.
Hätten wir also eine Aufgabe, die herkömmlich Jahre dauern würde, und hätten wir dazu ein Quanten-Computer, der sie alternativ mit exponentieller Beschleunigung löst, könnten wir die Aussage so akzeptieren. Allerdings gibt es noch nicht viele Algorithmen für Quanten-Computer, die in dieser Form praktische verwendbar sind. Was nicht zuletzt auch an der Größe und "Sensibilität" heutiger QC liegt.
Ein relevantes Beispiel, das immer wieder als "Gefahr durch Quanten-Computer" zitiert wird, ist das Verfahren von Shor, mit dem man einen wichtigen Schritt beim "Knacken" von besten heutigen Verschlüsselungsverfahren in akzeptabler Zeit durchführen kann. Um das zu verstehen, braucht es aber schon mehr Einsicht in die zugrunde liegende Mathematik. Daher wird hier meist nur der (befürchtete) Effekt zitiert und auf Verständnis verzichtet.
"Quanten-Rechner werden herkömmlichen Rechnern überlegen sein"
Man spricht auch generell von Quanten-Überlegenheit (Quantum Supremacy). Trotz der beängstigent klingenden Bezeichnung handelt es sich hier um eine unspektakuläre Sache. Es bedeutet lediglich das Ereignis, dass es eine Berechnung gibt, die ein Quanten-Computer schneller als jeder herkömmliche Supercomputer durchführen kann. Dabei ist es erst einmal egal, ob diese Berechnung einen Sinn macht oder praktische Bedeutung hat. Wie man kürzlich lesen konnte, hat man (mit einem QC von Google) bereits eine solche Berechnung durchführen können, d.h. der Meilenstein Quantum Supremacy ist schon erreicht.
"Jedes zusätzlich Qubit verdoppelt die Leistungsfähigkeit des Systems"
Hier bleibt einerseits unklar, was mit Leistungsfähigkeit gemeint ist - Rechenleistung, Speicherleistung, Leistung eines Algorithmus, der ein Qubit mehr zur Verfügung hat? Auch wenn wir einen Bit-Speicher (Register) um ein Bit erweitern, also von n auf n+1 Bits, können wir damit 2**(n+1) = 2*2**n Werte speichern bzw. mehr oder längere Befehle ausführen. So hatte sich auch die Prozessorarchitektur von früheren 32 Bit auf 64 Bit bei herkömmlichen Computern verändert und dabei prinzipiell eine 32-fache Verdoppelung der Leistung ermöglicht.
Was macht nun ein Qubit mehr aus bei einem Quanten-Computer? Zum einen gibt es dann doppelt so viele Basiszustände. Z.B. von 8 bei einem 3-Qubit System auf 16 bei 4 Qubits. In Superposition können damit 16 statt nur 8 Koeffizienten (Amplituden) einen Zustand bestimmen. Diese Verdoppelung ist analog der Situation bei Bits und wir hatten das schon oben bei N vs log(N) erklärt.
Zum anderen wissen wir, dass - ganz ander als beim Bit-Computing - verschränkte Zustände eine wichtige Rolle im Qubit-Computing spielen. Man kann sich also fragen, was bringt ein zusätzliches Qubit für die möglichen Verschränkungen, oder allgemein für die möglichen "Konfigurationen" von Superpositionen. Anders ausgedrückt: wieviel mehr Möglichkeiten gibt es für Zustände, in denen nur ein Basiszustand vertreten ist, oder zwei, oder drei usw. - unabhängig von den Werten der Amplituden. Diese Zahl wächst offenbar kombinatorisch. Für n=2 sind die "Muster" noch überschaubar: 4 mal |x>, 6 mal |x>+|y>, 3 mal |x>+|y>+|z> und 1 mal |x>+|y>+|z>+|v>, wenn |x>,|y>,|z>,|v> die Basiszustände |00>, |01>,|10>,|11> durchlaufen.
In Q13 (Superdichte Codierung) haben wir einen anderen Verdopplungseffekt gesehen: die Kapazität, Bitketten in GHZ-verschränkten Qubits zu "speichern" bzw. zu übertragen. Hier brachte jedes weitere Qubit in einer solchen Verschränkung eine Verdoppelung der Anzahl übertragbarer Bitketten.
Zuletzt eine Anmerkung: Bei "Was man so liest" fragt man sich leicht, wo man das gelesen hat. Die konkreten Aussagen in den Überschriften sind keine echten Zitate, obwohl sie so oder in Variationen der Wortwahl tatsächlich vorkommen. Wir wollen hier aber kein "Bashing" anzetteln, sondern nur kostruktiv klären, was dahinter steckt oder wo man leicht fehlgeleitet wird. Daher verzichten wir auf Quellenangaben.
Q15 Ein Geheimnis mit einer Frage rauskriegen - Bernstein-Vazirani-Algorithmus
In diesem Abschnitt wollen wir heraus finden, was es mit Quanten-Parallelismus und der viel zitierten Super-Beschleunigung von Quanten-Algorithmen auf sich hat. Wir bleiben dabei wieder auf dem Boden der Qubits und werden hier insbesondere wieder von einem Effekt Gebrauch machen, den wir in Q9 schon kennen gelernt hatten, dem (phase) Kickback.
Zur Lösung einer Aufgabe kann es durchaus verschiedenene Algorithmen geben und diese können sich darin unterscheiden, wieviel Aufwand es macht, um die Aufgabe zu lösen. Den Aufwand misst man meist in der benötigten Anzahl von Rechenschritten, Funktionsauswertungen, Entscheidungen usw. und charakterisiert den algorithmischen Aufwand dann in Bezug auf die "Größe" der Aufgabe. Bei einer Sortieraufgabe kann diese z.B. die Anzahl n der zu sortierenden Dinge sein.
Denken wir uns z.B. ein einfaches "binäres" Labyrinth. D.h. es gibt einen Eingang, danach gibt es Verzweigungen, bei denen man links oder rechts gehen kann und nach n Verzweigungen kommt man an eine Tür. Alle Türen bis auf eine, dem Ausgang, sind verschlossen. Eine naive Methode, das Labyrinth zu "knacken" wäre, immer vom Eingang loszulaufen und alle möglichen Wege auszuprobieren, bis man an den Ausgang kommt. Und irgendwann erwischt man ja den richtige Weg. Dieser nicht-so-clevere Algorithmus kann also die Aufgabe lösen. Aber wie hoch ist der Aufwand? Wenn man Glück hat, ist schon der erste Weg der richtige, wenn man Pech hat, der letzte. Also: schlimmstenfalls muss man 2^n Wege ausprobieren.
Orakel und Geheimnisse
Ein Orakel ist etwas, das ein Geheimnis kennt und das man dazu befragen kann. Zum Beispiel das Ergebnis eines WM-Fussballspiels. In der Qubit-Welt wird ein Orakel etwas abstrakter verstanden, als Black-Box oder eine Funktion mit unbekannten Größen (dem Geheimnis), die man durch Berechnung der Funktionswerte (Antworten) für verschiedene Eingabewerte (Fragen) herausfinden will. So kann man die Aufgabe "Gleichungen mit zwei Unbekannten" auch als Orakel auffassen, was bei vielen auch im übertragenen Sinne ein ewiges Orakel ist.
Nehmen wir an, es gibt ein Orakel, das den richtigen Weg kennt aber geheim hält. Das Geheimnis ist eine Kette von 0 und 1, wobei 0 für "links abbiegen" steht und 1 für "rechts abbiegen". Die Bit-Kette beschreibt damit den Weg vom Eingang bis zur richtigen Tür, dem Ausgang. Wer die 0-1-Kette kennt, kennt den Weg durch das Labyrinth.
Wie kann man diese Bit-Kette herausfinden?
Das erste Orakel
Man könnte alle möglichen n Bit langen 0-1-Ketten aufschreiben und einzeln dem Orakel vorlegen, bis es eine 1 (für richtig) als Antwort gibt. Das entspricht dem Aufwand unserer Wegsuche am Anfang: schlimmstenfalls müssten wir 2^n mal fragen. Der Algorithmus ist naheliegend und klassisch einfach zu beschreiben:
Für alle 0-1-Ketten der Länge n, von 000...0 bis 111...1, vergleiche bit-weise mit der geheimen Bit-Kette. Zähle die Übereinstimmungen. Sobald eine 0-1-Kette n Übereinstimmungen liefert, ist das Geheimnis gefunden. Ende.
Wir gönnen uns hier den Spaß und die Übung, dieses Vorgehen als einen Qubit-Algorithmus mittels Composer darzustellen. Etwa so:
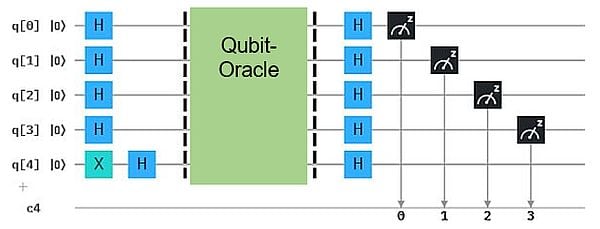
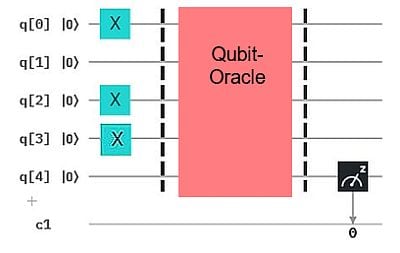Hier ist n=4 und die vorgelegte 0-1-Kette ist 1011, generiert mittels X-Gates. Das Orakel ist als Qubit-Orakel konstruiert und für uns nicht sichtbar. (Noch nicht. Weiter unten lüften wir die Abdeckung und sehen, wie das Orakel als Qubit-Algorithmus aussieht.) Qubit q4 übernimmt die "Antwort" des Orakels, das wir durch Messung sichtbar machen. Wenn wir die richtige Bit-Kette als Input vorgelegt haben, bekommen wir hier (zu 100% der Wiederholungen) eine 1 als gemessene Antwort. Für jede andere Bit-Kette dagegen ein "gemischtes" Messergebnis, d.h. eine Häufigkeitsverteilung über 0 und 1.
Wenn wir in diesem Beispiel alle Inputs ausprobieren, finden wir, dass das Geheimnis 0110 ist. Je nachdem, wie wir vorgehen, kann das maximal 2^n = 16 Versuche bedeuten.
Das zweite Orakel
Eine bessere Möglichkeit ist es, alle Bit-Ketten mit nur einer 1 aufzuschreiben und zu fragen, ob es an gleicher Position auch eine 1 in der geheimen Bit-Kette gibt, also eine Art Filterverfahren.
Für alle 0-1-Ketten, die an nur einer Position eine 1 haben und sonst 0, multipliziere jedes Bit mit dem entsprechenden Bit der geheimen Bit-Kette und bilde die Summe dieser n Produkte. Ist das Ergebnis 0, gibt es an der betreffenden Stelle keine 1 in der geheimen Bit-Kette, sondern eine 0. Und umgekehrt. Sind alle n Positionen durchlaufen, hat man die geheime Bit-Kette rekonstruiert.
Auch hier gönnen wir uns den Spaß, statt des klassischen Algorithmus ein Qubit-Orakel zu konstruieren.
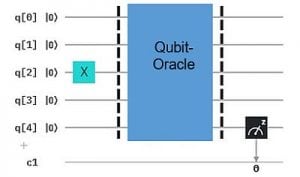Viel Neues ist nicht zu sehen, da wir das Orakel wieder geheim halten. Weiter unten sehen wir, wie einfach der Qubit Algorithmus dazu ist. Hier "prüfen" wir das 3. Bit des Geheimnisses mit dem Input 0010. Die Messung von q4 liefert eine 1, wenn an der 3. Position eine 1 steht (hier der Fall). Haben wir das X-Gate für alle 4 Qubits verwendet, haben wir alle 4 Positionen in der geheimen Bit-Kette bestimmt.
Es sind also insgesamt nur n=4 "Fragen" an das Orakel zu stellen, um das Geheimnis aufzudecken - gegenüber 16 beim ersten Algorithmus. Weil 2^n eine Potenz zur Basis 2 ist, bei der n der Exponent ist, spricht man dem zweiten Algorithmus eine exponentielle Verbesserung (Beschleunigung) im Vergleich zum ersten zu: n zu 2^n. Wer sich mit Logarithmen auskennt, kann auch schreiben: log(n) zu n*log(2).
Beides sind klassische Algorithmen. Das Zweite ist gleichzeitig auch das beste klassische Verfahren, um diese Aufgabe zu lösen. Auch wenn wir sie als Qubit-Algorithmen darstellen, steckt da noch nichts Qubit-Typisches dahinter. Anders wird es mit dem nächsten Verfahren, dem sog. Bernstein-Vazirani-Algorithmus. Der macht u.a. von Superposition und (phase) Kickback Gebrauch.
Bernstein-Vazirani-Algorithmus
Der Gedanke ist eigentlich ganz einfach: statt das Orakel mit einzelnen Bit-Ketten zu befragen und die Antworten zu notieren, könnten wir doch einen typsichen n-Qubit-Zustand erzeugen, in dem die Zustände |0> und |1> jeweils gleichermaßen vertreten sind, und diesen dem Orakel vorlegen. Das Orakel soll dann entscheiden, "was richtig ist" - im Vergleich mit dem Geheimnis.
Zugegeben, ganz so einfach ist es nicht - auch wenn man immer wieder liest, dass ein Qubit "0 und 1 gleichzeitig" sein kann. Aber wir können als Input für das Orakel die n Qubits mittels Hadamard-Gates in die bekannte Superposition aus (1,0) und (0,1) versetzen. Damit beginnt der Algorithmus, der Bernstein und Vazirani als Entdecker (1992) zugeschrieben wird. Im Composer mit n=4 sieht das so aus:
Hier ist q4 wieder ein "Hilfs-Qubit", das, anders als die Input-Qubits, per X-Gate mit (0,1) initialisiert wird (als Ket: |1>). Wie die geheime Bit-Kette hier im Qubit-Orakel angelegt ist, finden wir gleich heraus. Der Algorithmus bringt also zunächst mittels H-Gate alle Qubits in die Hadamard-Superposition. Am Ende werden die Qubits per H-Gates wieder in Basis-Zustände (1,0) oder (0,1) versetzt und gemessen. Das Hilfs-Qubit ist dabei unwichtig, d.h. auf das H-Gate und die Messung kann man verzichten.
Zum Unterschied zu den klassichen Algorithmen wird dem Orakel hier nicht eine Bit-Kette der Länge n als Input vorgelegt, sondern ein n-Qubit-Zustand! Betonung auf "Zustand" und "ein". Die Antwort des Orakels auf diesen Zustand bewirkt eine Änderung des n-Qubit-Zustands. Werden darauf dann H-Gates angewandt, besteht der Endzustand aus Basis-Zuständen, die durch Messung eine Bit-Kette ergeben. Und diese enstpricht genau dem Geheimnis des Orakels. Kaum zu glauben.
Wenn also die Messung der 4 Qubit-Zustände 0101 ergibt, dann ist das die gesuchte Bit-Kette, die Lösung, der Geheim-Code, der Weg durch's Labyrinth, oder was auch immer das Geheimnis bedeutet.
Vergleichen wir die Anzahl der Fragen, die wir dem Orakel im stellen müssen, so haben wir beim ersten Algorithmus im schlechtesten Fall 16, beim zweiten immer 4 Fragen zu stellen, und beim Bernstein-Vazirani nur eine. Das Verhältnis zum besten klassischen Algorithmus ist also 1 zu n. Wir haben hier also für große n eine erhebliche algorithmische Verbesserung. In Q16 "Was man so liest" werden wir die Bedeutung dieses Effektes noch weiter diskutieren. Hier wollen wir zunächst noch verstehen, wie und wodurch dieser Effekt zustande kommt.
Das Orakel und das Phase Kickback
Den zentralen Trick dieses Algorithmus wollen und können wir bereits am einfachsten Problembeispiel verstehen: einer geheimen Bit-Kette der Länge 1. (Dieser Trick ist sehr verständlich dargestellt von M. Treinish in seinem Vortrag "Open Source Quantum Computing" . Als Youtube video: https://youtu.be/th4TDYX6xoc - 2019, englisch.)
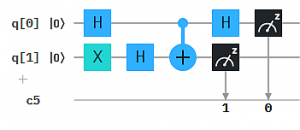In Q9 hatten wir den (Phase) Kickback Effekt schon demonstriert. Das Composer-Diagramm sah so aus (s. Abb. links). Es erinnert, zumindest am Anfang, an das vorige Composer Diagramm, allerdings mit nur einem Input-Qubit und ohne das zweite H-Gate beim Hilfs-Qubit.
Wir haben inzwischen gelernt, die Zustandsänderungen im Algorithmus zu verfolgen, so dass wir den Effekt des Kickback nachvollziehen können. Wir bezeichnen die Koordinaten der Qubit-Zustände von q0 und q1 mit (x,y) bzw. (u,v). Die Ausgangszustände sind (x,y) = (1,0) und (u,v) = (0,1) (nach dem X-Gate).
| (u,v)⊗(x,y) | ux | uy | vx | vy | Koordinaten q1,q0 |
| Kets | |00> | |01> | |10> | |11> | |
| (0,1)⊗(1,0) | 0 | 0 | 1 | 0 | |
| H(0,1)⊗H(1,0)=1/2(1,-1)⊗(1,1) | 1 | 1 | -1 | -1 | (Vorfaktor 1/2) |
| CNOT q0-q1 (vertauscht uy,vy) | 1 | -1 | -1 | 1 | =1/2(1,-1)⊗(1,-1) |
| 1/2(1,-1)⊗H(1,-1)=1/√2(1,-1)⊗(0,1) | 0 | 1 | 0 | -1 | =H(0,1)⊗(0,1) |
Der Zustand von q0 ist damit (x,y) = (0,1), der von q1 ist H(0,1), also unverändert. Qubit q1 hat auf diese Weise seinen Ausgangszustand (0,1) auf q0 übertragen (q1 kicked back). DIe Messung für q0 ergibt eine 1. Und das liegt letztlich an dem CNOT. Würden wir dieses weg lassen, gäbe es die Vertauschung von uy und vy nicht. Die H-Gates auf der q0-Linie würden sich aufheben, der Zustand von q0 bliebe unververändert, der von q1 bliebe H(0,1). Die Messung von q0 würde 0 ergeben.
In der Ket-Darstellung sehen die Zeilen 4 und 5 wie folgt aus
(|0>+|1>)(|0>-|1>) = |00>-|01>+|10>-|11> ---CNOT--- |00>-|01>+|11>-|10> = (|0>-|1>)(|0>-|1>)
Das erinnert an die Binomischen Formeln: Links die 3., rechts die 2. Das CNOT verändert die Dritte in die Zweite.
Jetzt bemerken wir Folgendes:
Eine Kickback-Struktur zwischen Input-Qubit und Hilfs-Qubit wird vom Bernstein-Vazirani-Algorithmus offenbar als 1 erkannt, eine fehlende als 0. Wenn der Algorithmus also eine n lange geheime Bit-Kette mit Hilfe eines n-Qubit-Zustands erkennen soll, muss man nur entsprechende Kickback-Strukturen (d.h. die CNOT-Gates) hintereinander schalten. Und zwar so, das die Position einer 1 im Geheimnis dem Control-Qubit entspricht.
Hier ist das Beispiel mit "aufgedecktem" Orakel. Das Geheimnis ist 0101 (oben ist rechts) und wird korrekt gemessen bei einem Durchlauf mit dem Simulator.
Einsatz eines echten Quanten-Computers: IBMQX2
Bisher haben wir die Qubit-Algorithmen immer auf dem Q-Simulator ablaufen lassen. Zeit für einen echten Quanten-Computer!
Wir lassen den gleichen Composer Circuit für den Bernstein-Vazirani-Algorithmus nun auf dem IBM-Quanten-Computer IBMQX2 laufen.
Die Anzahl Wiederholungen (number of shots) konnte beim Simulator auf 1 gesetzt werden, da wir erwarten konnten, dass das Ergebnis zu 100% genau eine Bit-Kette liefert. Wird stattdessen ein Quantum-Device verwendet, muss man damit rechnen, dass aufgrund von Dekohärenz-Effekten das Ergebnis eines einzelnen Durchlaufs "gestört" ist. Mit z.B. n_shots=1024 wird das Programm 1024 Mal wiederholt und man kann aus der Häufigkeit der Ergebnisse die richtige Antwort erschliessen. Es ist, als müssten wir das Orakel mehrfach befragen, weil es die Antwort immer "leicht verwirrt" gibt. (Ein typischer Diskussionspunkt, wenn es um die (theoretische) "Quanten-Beschleunigung" geht.)
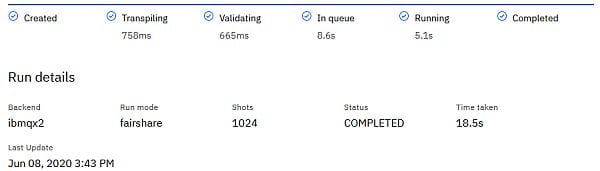
Hier zunächst das Ablaufprotokoll:
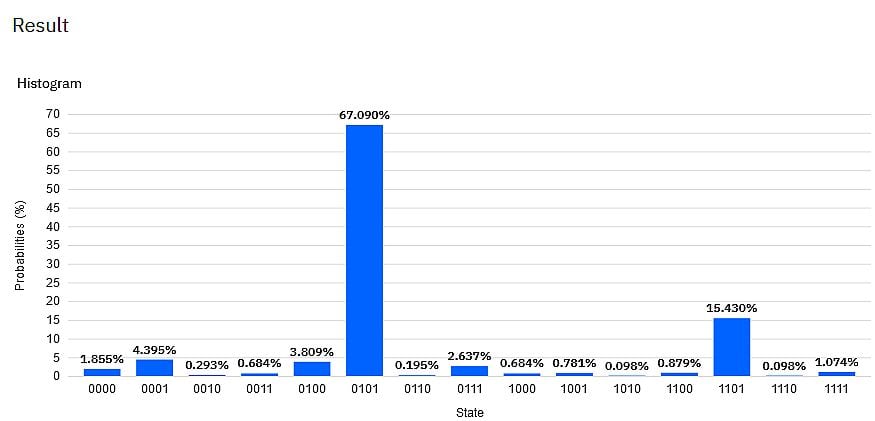
Und hier das Ergebnis der 1042 Durchläufe auf dem ibmqx2:
Wir sehen hier, dass das bei weitem häufigste Messergebnis die Bit-Kette 0101 ist, die wir als gefundenes Geheimnis akzeptieren. Sie stimmt auch mit dem Ergebnis des Simulators überein. Mit geringen Anteilen werden aber auch alle anderen möglichen 4-Bit-Ergebnisse gemessen, ein Effekt, der (zur Zeit) bei echten Quanten-Computern auftritt und kompensiert werden muss. Um diese "Unsicherheit" zu eliminieren, bleibt uns hier (in dieser Blog-Serie) nur die Wiederholung.
Die ersten beiden Algorithmen "aufgedeckt"
Und da wir gerade dabei sind, decken wir auch die Orakel der beiden klassischen Algorithmen auf:
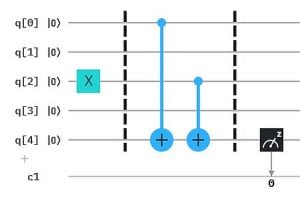Der zweite Algorithmus (blau), der mit n Fragen ebenfalls das Geheimnis 0101 findet. Als Input wird in der Abbildung per q2 das 3. Bit (von rechts) geprüft.
Und hier der erste Algorithmus (pink):
Das Orakel des ersten Algorithmus soll ja beantworten, ob die Zustände des n-Qubit-Inputs der geheimen Bit-Kette entsprechen oder nicht. Was wir hier sehen, ist eine naive Methode, diese Antwort über das Hilfs-Qubit q4 zu generieren: Das Orakel "zählt" die Anzahl der Übereinstimmungen durch "Drehungen" (cRz - Controlled Rz) des Hilfs-Qubit-Zustands um einen (kleinen) Winkel, hier pi/6. Am Ende wird der Zustand um das n-Fache des Winkels "zurückgedreht" (Rz-Gate). Waren alle n Inputs "richtig", führt das Zurückdrehen das Hilfs-Qubit auf den Basiszustand zurück. Ansonsten auf einen Superpostionszustand. Im Beispiel sind die Zustände der Input-Qubits gerade so, dass alle mit der im Orakel angelegten Bit-Kette 0110 übereinstimmen. Das Messergebnis (wiederholte Durchläufe) ist 1 zu 100%.
(Anm.: Das Rz- und cRz-Gate haben wir bisher nicht behandelt, weil wir im Wesentlichen ohne dem auskommen. Wir kennen das Z-Gate. Rz und Controlled Rz erzeugen winkelabhängig "Teilschritte" von Z in Form von Drehungen. Um sie in unserem Circuit wirksam zu machen, müssen wir vorher den Basis-Zustand von q4 mit dem H-Gate transformieren - und am Ende rück-transformieren. Etwas kompliziert, aber es funktioniert. Alternativ kann man auch ein "controlled Ry" durch eine Kombination von mehreren Gates implementieren, was hier aber unnötig unübersichtlich würde.)
Wie geheim ist geheim?
Im Composer Diagramm zum Bernstein-Vazirani Algorithmus scheint es zunächst etwas unsinnig, das Orakel zu befragen, wenn die "geheime Bit-Kette" im Circuit-Teil für das Orakel doch ganz offensichtlich ist: 1, wo ein CNOT angelegt ist, 0 sonst.
Zum einen ist es immer so, dass, wenn man eine Übereinstimmung von zwei Dingen prüfen will, beides irgendwie "zur Verfügung" haben muß. So auch, wenn man eine unbekannte Bit-Kette durch Inputs herausfinden will. Auch die unbekannte Bit-Kette muß "irgendwie" verfügbar oder überprüfbar vorliegen. Die Form kann beliebig kompliziert sein oder so einfach wie eine klassische binäre Daten-Variable - oder eben ein Teil eine Qubit-Circuits.
Zum anderen kann man sich vorstellen, dass der Orakel-Teil des Circuits "unerkannt" implementiert wird, etwa durch einen Algorithmus außerhalb des eigentlichen Bernstein-Vazirani-Circuits. In der Qubit-Programmierumgebung Qiskit kann man z.B. in einer Funktion eine zufällige Bit-Kette erzeugen, die dann in einen Programmblock für das Orakel umgesetzt wird. Damit ist das Orakel innerhalb des Gesamt-Algorithmus eine Black Box.
Generieren eines zufälligen Orakels - mit Qiskit
Wir zeigen und erklären zum Abschluss diese Aufgabe für eine unbekannte, zufällige Bit-Kette der Länge n= 32 anhand eines vollständigen Python Programms unter Verwendung der Qiskit-Umgebung. Der Algorithmus wird also insgesamt in einer Programmiersprache beschrieben, statt umgangssprachlich oder grafisch per Composer Diagramm. Die Qiskit Ausdrücke entsprechen den Komponenten eines Composer Circuits; man kann sich sogar das Qiskit Programm als Composer Grafik anzeigen lassen. Python/Qiskit Programme kann man am besten als sog. "Notebooks" direkt in der IBM Q Experience Cloud entwerfen und ausführen - auf dem QC-Simulator oder einem realen QC. (Notebooks sind eine Kombination aus Text- und Programm-Teilen. Man kann also im Klartext die "Story" zum Programm in einzelnenen Schritten aufschreiben und dazu die Programm-Teile einfügen. Alles zusammen ist dann ablauffähig. Die Dateiendung der Notbooks ist .ipynb - für iPython NoteBook.) Zum Testen von Teilen oder einzelnen Ideen kann man immer auch auf den Composer zurückgreifen, denn die "Übersetzung" eines Composer Circuits nach Qiskit ist simpel.
Wir empfehlen hiermit auch den Übergang vom Composer (grafisch) zu Qiskit/Python (Programmierung). Mit Qiskit/Python ist man viel flexibler in der Formulierung von Qubit-Algorithmen. Außerdem kann man damit gut die Kombination von konventioneller Algorithmik und Qubit-Algorithmik gestalten, d.h. den Quanten-Computer nur für seine speziellen Stärken einsetzen.
Unter diesem Link: " Bernstein-Vazirani-Algorithmus" kann man das komplette Notebook als html-Datei herunterladen bzw. ansehen. Möchte man mit dem Notebook im IBM-Q Umfeld experimentieren, kann man die Datei in der IBM-Q Umgebung in ein leeres Qiskit-Notebook hineinkopieren (Text-Zellen getrennt von Code-Zellen).
Hier beschreiben wir nur die wesentlichen Teile in Text-Form.
- Defintion eines Qubit-Systems namens 'circ' mit n=33 Qubits und Mess-Bits
- 32 für das Geheimnis und 1 Hilfs-Qubit
- Die Gates werden je Qubit eingesetzt
- X-Gate für das Hilfs-Qubit q[32]: circ.x(q[32])
- H-Gate für alle Qubits von q[0] bis q[32]: circ.h(q[i])
- Das Geheimnis wird generiert und das Orakel eingefügt
- Zufällige 0-1-Kette (das Geheimnis) wir erzeugt
- Für alle Positionen s mit 1 in der Kette wird das entsprechende Qubit mit einem CNOT versehen: circ.cx(q[s],q[32])
- Die Gates je Qubit werden ergänzt
- H-Gate für alle Qubits von q[0] bis q[32]: circ.h(q[i])
- Mess-Operation
- Messen der Zustände der Qubits: circ.measure(q,c)
- c enthält die Bit-Ergebnisse (von rechts nach links)
- Das c-Bit ganz links gehört zum Hilfs-Qubit und wird ignoriert
- Das Qubit-Programm wird ausgeführt
- Die "Backend-Maschine" wird aufgerufen (Simulator oder ein realer Quanten-Computer)
- Die Anzahl Wiederholungen ('shots') wird festgelegt: n_shots=1
- Das Programm wird gestartet: job=execute(circ, ....)
- Das (Mess-)Ergebnis wird erstellt: result=job.result()
- Das Ergebnis 'result' wird aufbereitet
- Die Ergebnis-Bit-Kette wird als Lösung des Geheimnisses ausgegeben.
Ein Beispiel für die Ergebnis-Ausgabe des Programms:
Anm.: Ergebnisse für Qubits q0 bis q32 werden in der Bit-Kette von rechts nach links geschrieben
Qubits, die nicht gemessen werden, haben den Messwert 0 per Default
counts: {'100101100111110100101111010110000': 1}
Gefundenes Geheimnis: 00101100111110100101111010110000
Das Orakel war: [0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0]
Mit diesem Ausflug in die Qiskit-QC-Programmierung öffnen wir das Feld für weitere, neue Versuche, Qubit-Algorithmen zu entwerfen, zu realisieren bzw. nachzubauen. Es sei aber noch einmal daran erinnert, dass die Qubit-Welt über das, was wir hier dargestellt haben, hinaus noch weitere mathematische Begriffe und Methoden kennt und verwendet. D.h. nicht alle Algorithmen, die sich in der Literatur oder in Einführungs-Videos finden, sind mit unserer "Schul-Qubit-Toolbox" realisierbar oder verstehbar.
Im nächsten Abschnitt der Blog-Serie wollen wir versuchen zu verstehen, was so alles in den Medien und populärwissenschaftlichen Beiträgen zum Quanten-Computing geschrieben wird. Zu "Was man so liest" geht es hier.
Zum Schluss wieder die Tabellen-Ergänzung mit neuen Begriffen:
| Begriff englisch | Begriff deutsch | Bedeutung |
| Oracle | Orakel | Black box, Qubit-Funktion mit (unbekannten) Parametern |
| Secret | Geheimnis | (Unbekannte) Parameter des Orakels, meist Bit-Ketten |
| Exponential improvement | Exponentielle Verbesserung | Auch als "Beschleunigung" bezeichnet. Aufwand eines Algorithmus im Vergleich zu einem anderen im Verhältnis log(n) zu n, wobei n die "Größe" des Problems kennzeichnet. Auch n zu 2^n. |
| Number of shots | Anzahl Wiederholungen | Wiederholungen eines Durchlaufs, um eine statistische Verteilung über die möglichen Messergebnisse (Bit-Ketten) zu erhalten |
| Decoherence | Dekohärenz | Ungesteuerter Zerfall von (Mehr-)Qubit-Zuständen auf einem realen physikalischen Gerät (Quanten-Computer) |
| ibmqx2 | ibmqx2 | Realer Quanten-Computer, offen zugänglich in der IBM Q Cloud |
| Rz, cRz | Rz, cRz | Weiteres Gate bzw. Controlled Gate mit Rotationswirkung |
| Qiskit | Qiskit | Q-Bibliothek zur Einbettung in (z.B.) Python. Professionelle Alternative zur grafischen Programmierung mit dem Composer |
| Notebook | Notebook | Skripte kombiniert aus aus Text- und Programm-Teilen (Zellen) |
| Cells | Zellen | Notebook-Abschnitte, die Text oder Programm-Code enthalten und einzeln oder zusammen ausgeführt werden können |
| Ancillary Qubit | Hilfs-Qubit | Extra Qubit, das für den Algorithmus gebraucht wird aber nicht in das (Mess-)Ergebnis eingeht |
Q14 Quanten-Teleportation
Die geheimnisvolle Kunst des Teleportierens kennt man - je nach Alter - aus Raumschiff Enterprise ("Beam' mich hoch, Scotty!") oder als Zauber aus Harry Potter (Disapparieren und Apparieren). Hier wie da verschwindet etwas oder jemand und taucht an anderer Stelle wieder auf. Der "3D-Druck" tut im Effekt etwas Ähnliches, nur verschwindet das Original nicht, wenn eine Kopie des Objekts an anderer Stelle "erscheint". Lediglich die (geometrischen) Daten des Original-Objekts werden an die Empfangsstelle übertragen. Quanten-Teleportation ist beides - oder beides nicht: das Original-Qubit verschwindet und taucht an anderer Stelle als neues Qubit-Objekt auf. Dazwischen wird Information übertragen.
Etwas ernsthafter: Als Quanten-Teleportation bezeichnet man die Übertragung eines Qubit-Zustands mittels klassicher Bit-Information, um ein anderes Qubit in den Zustand des Originals zu versetzen. Dabei geht der Original-Zustand verloren. Und da Qubits keine "Individualität" haben, hat man vorher und nachher das gleiche Qubit, nur an einem anderen Ort. Teleportation eben. Das funktioniert tatsächlich auch technisch und wurde schon über viele Kilometer hinweg realisiert wie ein Blick ins Wikipedia zeigt.
Die Quanten-Teleportation ist das Gegenstück zur Quanten-Kommunikation (s. Q13): Die Quanten-Kommunikation übermittelt zwei Bit Information mittels eines Qubit-Zustands, die Quanten-Teleportation übermittelt einen Qubit-Zustand mittels zweier Bits. Und in beidem spielt die Verschränkung eine entscheidende Rolle.
Das Teleportationsverfahren schrittweise von der Ausgangssituation her zu entwicklen, wird leicht mühselig, auch für den Leser. Daher schlagen wir dieses Mal den umgekehrten Weg ein: Wir stellen den Algorithmus vor, experimentieren damit ein wenig und liefern die Erklärung weiter unten nach, als systematische Darstellung der Zustandsabfolge.
Teleportation - der Algorithmus
Der Ablauf ist schnell erzählt: Alice möchte Bob den Zustand ihres Qubit (q0) übermitteln. Bob erzeugt dazu ein Qubit-Paar (q1, q2) mit der üblichen Verschränkung (siehe Circuit 7) und schickt das eine davon (q1) an Alice. Das andere verbleibt bei Bob. Alice wendet auf ihre beiden Qubits (q0, q1) zwei Gates an, ein CNOT von q0 zu q1 und danach ein H-Gate auf q0.Anschließend misst sie die Zustände der beiden Qubits. Die beiden Bits aus der Messung schickt sie auf dem klassichen Übertragungsweg an Bob. Der steuert damit ein X- und ein Z-Gate, die auf den Zustand seines Qubits (q2) wirken. Als Ergebnis erhält er q2 in dem Zustand, in dem q0 zuvor war. Wie man das nachprüft, sehen wir anschließend.
Im Composer sieht die Teleportation wie folgt aus:
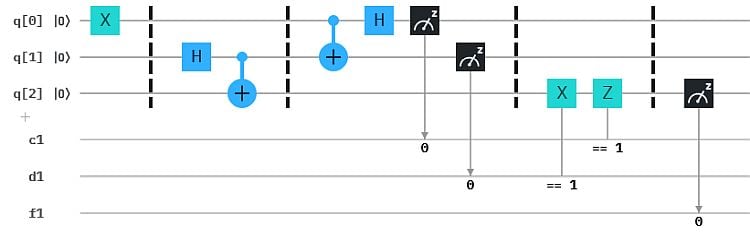Dieses Composer-Bild hat drei 1-Bit Linien, für jede Qubit-Messung eine. Bisher hatten wir die Messbits von Multi-Qubit-Systemen immer auf einer "Schiene". Der Vorteil hier ist, dass wir die Messbits unabhängig voneinander zur Steuerung einsetzen können, statt über die 3-Bit Binärzahl-Werte zu steuern. Man sieht das an den bedingten X- und Z-Gates.
Die Barrieren (gestrichelte Linien) dienen hier nur zur grafischen Gliederung: Links definiert Alice den Zustand von q0, der teleportiert werden soll. Hier (0,1). Im zweiten Abschnitt erzeugt Bob ein verschränktes Qubit-Paar, wovon er q1 an Alice schickt. Im mittleren Abschnitt wendet Alice auf ihre Qubits ein CNOT und ein Hadamard-Gate an und misst das Ergebnis. Das Ergebnis von q0 wird auf das Bit c1 übertragen, das von q1 auf d1. Alice sendet diese klassichen Bits an Bob. der wendet Bit-controlled Operationen (X, Z) auf sein Qubit an. Wenn der Zustand von q1 als 1 gemessen wird, wird das X-Gate auf q2 angewendet. Wird für q0 eine 1 gemessen, wird das Z-Gate angewendet. Sind beide Messbits 1, dann wirken beide Gates. Abschließend wird q2 gemessen. Wenn alles gut gegangen ist, müsste q2 nun im Zustand (0,1) sein.
Wir starten den Algorithmus und bekommen als Ergebnis z.B. 110 bei einem Durchlauf. Ok, für q2 wird eine 1 gemessen. Die Logik: Wenn q2 nach Teleportation im Zustand (0,1) ist, darf eine Messung keine 0 ergeben. Mit 1024 shots bekommen wir dieses Histogramm:
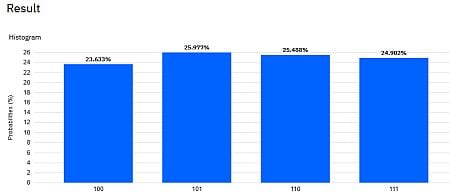Alle Messergebnisse liefern eine 1 für q2. Interessant ist auch zu bemerken, dass q0 sowohl 1 als auch 0 liefert. D.h. q0 hat seinen ursprünglichen Zustand verloren, der nur das Messergebnis 1 hatte.
Wenn Alice q0 im Zustand (1,0) teleportieren will, entfällt das X-Gate am Anfang. Das Ergebnis-Histogramm zeigt, wie zu erwarten, dann nur 3-Bit-Ketten, die links eine 0 haben. Klar!
Damit haben wir die Basiszustände teleportiert.
Teleportation allgemeiner Qubit-Zustände
Wenn wir einen beliebigen Qubit-Zustand als Superposition der Basiszustände (1,0) und (0.1) teleportieren wollen, können wir eigentlich davon ausgehen, dass, wenn diese korrekt teleportiert werden, auch ihre Kombination korrekt in q2 übertragen wird. Wir probieren das gleich mal aus.
Dabei machen wir uns die Darstellung des Messergebnisses von q2 etwas einfacher, indem wir nach der Teleportation q0 und q1 in den Standard-Anfangszustand versetzen und erneut messen. Etwas so:
Wir setzen statt X das Rotationsgate Ry mit dem Drehwinkel 30° an den Anfang von q0. Eine direkte Messung des Qubits in diesem Zustand ergibt, idealisiert, zu 75% Bit 0 und zu 25% Bit 1. Wir wollen sehen, ob nach Durchlauf des Circuits auch q2 diese Eregbnis liefert.
Mit der "Neutralisierung" von q0 und q1 am Ende des Circuits bekommen wir ein Histogram mit zwei Säulen, die sich nur im Messwert für q2 unterscheiden.
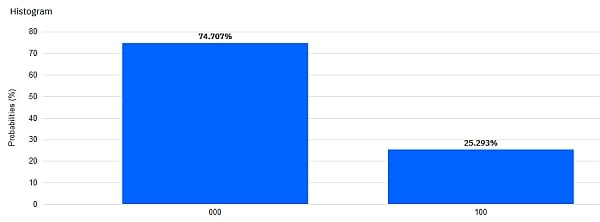Und wir finden tatsächlich insgesamt etwa 75% der Ergebnisse mit 0 und 25% mit 1 für das linke Bit. Also genau wie erwartet!
Qubit Zustände und Messergebnisse
Wir machen das gleiche mit dem Zustand 1/√2(|0>-|1>), der entsteht, wenn wir X --- H hintereinander auf |0> anwenden. Wie erwartet, ergibt die direkte Zustandsmessung von q0 das gleiche wie die Messung von q2 nach Durchlauf der Teleportation. Scheint also unsere Vermutung zu bestätigen. Scheint! Wir wollen aber nicht Messergebnisse teleportieren, sondern Qubit-Zustände. Können wir hier aus dem Ergebnis der q2-Messung schließen, dass tatsächlich der Zustand von q0 korrekt auf q2 übertragen wurde? Nein! Ein einfacher Versuch: mit dem Zustand H|0> =1/√2(|0>+|1>) (plus!) bekommen wir die gleichen Messergebnisse. Man kann also nicht sagen, ob die q2-Messung von dem ersten oder dem zweiten Teleportationsbeispiel stammt.
An dieser Stelle müssen wir uns noch einmal klarmachen, dass man zwar immer vom Zustand eines Qubit-Systems auf das Messergebnis schließen kann, aber aus einem Messergebnis nicht eindeutig auf den Zustand zurück schließen kann. Man sagt, die übereinstimmenden Messergebnisse sind eine notwendige Bedingung für die korrekte Teleportation, aber keine hinreichende. Wie können wir hier eine Unterscheidung herbei führen und festellen, ob die Teleportation gelungen ist?
Zwei Möglichkeiten stehen uns zur Verfügung. Erstens, die Abfolge der Zustandsänderungen dieses 3-Qubit-Systems Schritt für Schritt mittels der Formeln nachzuvollziehen und am Ende den tatsächlichen Zustand von q2 mit q0 zu vergleichen. Das "üben" wir am Ende des Blogs.
Als zweite Möglichkeit nutzen wir die grundsätzliche Umkehrbarkeit von Qubit-Operationen. Wenn wir nach der Teleportation erst noch ein Gate auf q2 anwenden, das das H-Gate umkehrt, und die Teleportation korrekt funktioniert hat, müssten wir im ersten Fall (X --- H) immer 1 als das linke Messbit bekommen, im anderen Fall 0. Im Beispiel-Fall ist H selbst ein komplementäres Gate, das wir direkt hinter der letzten Barriere eingefügt haben. (Alternativ könnte man auch Ry(3π/2) verwenden. Mal ausprobieren!) Aus diesen Messergebnissen können wir dann schließen, dass wir in q2 den Zustad |1> bzw. |0> vorliegen haben, und damit der mit H veränderte Zustand korrekt übertragen wurde. Das Umkehr-Verfahren komplementiert also das Messverfahren bei der Bestimmung von Zuständen.
Tatsächlich bekommen wir hier zu 100% die 1 für q2.
Anm.: Natürlich können auch die Basiszustände mit einem Minuszeichen versehen sein, z.B. per 180° Drehung und dabei 0 bzw. 1 als Messergebnis liefern. Dieser Faktor -1 macht aber nichts aus, denn die beiden Zustände im Beispiel unterscheiden sich ja schon über die Messergebnisse.
Teleportieren, Klonen, Kopieren, Übertragen
Warum das doch recht aufwändige Teleportieren, um ein "anderes" Qubit in den Zustand von q0 zu bringen? Kann man den Zustand nicht einfach kopieren wie bei "gewöhnlichen" Algorithmen? Beispiel: a = 5, b=a , dann haben wir zwei Variablen mit dem Wert 5 (wie auch immer dies in einer Programmiersprache umgesetzt wird).
Kopieren bedeutet eine Kopie herstellen, d.h. das Original bleibt erhalten, die Kopie ist etwas anderes als das Original. Klonen bedeutet, das Original noch einmal herstellen. Wenn wir den Zustand eines Qubits auf ein zweites Qubit kopieren wollten, würde wir es automatische klonen, denn es gibt nichts, was zwei Qubits voneinander unterscheiden könnte als der Zustand.
Nun gibt es in der Theorie der Qubits ein Theorem, das besagt, dass man Qubits nicht klonen kann, das sog. No-Cloning-Theorem (s. Wikipedia). Das ist nicht zu schwer zu beweisen, überschreitet aber den mathematischen Rahmen, in dem wir uns hier bewegen wollen. Wir müssen also akzeptieren, dass man nicht aus dem (beliebigen, unbekannten) Zustand eines Qubits ein zweites herstellen kann, ohne z.B. das Original zu zerstören. Natürlich kann man, wenn man den Zustand eines Qubits kennt und weiß, wie er "hergestellt" wurde, ein zweites Qubit mit Hilfe von Gates so präparieren, dass es den gleichen Zustand hat. Dazu muss man aber den Zustand des Originals explizit kennen!
Man kann aber den Zustand eines Qubits übertragen. Teleportation ist eine Methode. Eine ganz einfache Methode ist das Swap-Gate: es vertauscht die Zustände von zwei Qubits in einem Circuit. Man kann das so sehen, dass der Zustand von einem Qubit auf das andere übertragen wird und umgekehrt. In herkömmlichen Algorithmen sieht ein Variablen-Swap zwischen a und b so aus: s = a, a = b, b = s (nicht etwa: a=b, b=a !). Im Effekt haben wir aber nur die Qubit-Variablen getauscht.
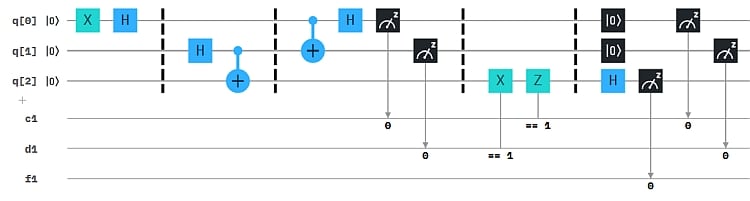
Eine echte Übertragungsmethode ist eine Art lokale Version der Teleportation. Lokal deshalb, weil hierbei keine Übertragung im Sinne eines Transports zwischen entfernten Orten (Alice und Bob) stattfindet. Der Composer-Circuit dazu sieht so aus:
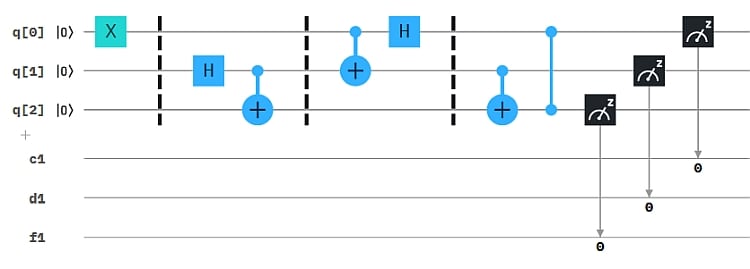Das Ergebnis Histogramm entspricht dem ersten oben, d.h. q2 liefert nur 1, die beiden anderen - insbesondere q0 - jeweils 0 und 1.
Statt Bit-controlled Gates wie bei der Teleportation haben wir hier ein CNOT (auch cX genannt) und ein cZ. Damit "kürzen" wir den Umweg über die Messwerte ab. Statt zu messen, ob q0 bzw. q1 eine 1 oder 0 liefern, und danach die Gates X und Z für q2 zu steuern, nehmen wir gleich die Zustände von q0 und q1, um die Gates zu steuern. Man beachte, dass dabei stillschweigend unterstellt wird, das z.B. Zustand |1> und Messung 1 äquivalent sind.
Der Unterschied zwischen Teleportation und lokaler Übertragung liegt in der "Anwendung" der Algorithmen. Bei der Teleporation werden Qubits an unterschiedlichen Orten behandelt und die Zustandsübertragung mittels klassicher Bits - und damit klassischer Übertragungsmedien - durchgeführt. Alice kann damit den Zustand eines Qubits, das sich bei ihr befindet, auf ein Qubit von Bob übertragen. Dagegen ist die lokale Übertragung - eben lokal.
Das Zustandsprotokoll
Wenn wir den Teleportationsalgorithmus schon nicht entworfen haben, wollen wir ihn wenigstens verstehen. Dazu versuchen wir die Entwicklung der Zustände des 3-Qubit Systems Schritt für Schritt anhand eines Zustandsprotokolls nachzuvollziehen. Dazu konstruieren wir uns eine Tabelle, die im Wesentlichen die 8 Koordinaten eines 3-Qubit als Spalten hat. Jede Zeile steht für einen Schritt im Algorithmus. Der jeweilige Schritt wird in der Zeile links symbolisch dargestellt. Rechts ist noch Platz für eventuelle Erläuterungen oder Hinweise. Die Zustandskoordinaten der Qubits q2, q1 und q0 werden mit (r,s), (u,v) bzw. (x,y) benannt. Wir wollen das erste Beispiel oben nachvollziehen, beginnen also mit dem X-Gate auf q0.
| (r,s)⊗(u,v)⊗(x,y) | rux | ruy | rvx | rvy | sux | suy | svx | svy | Koordinaten (q2,q1,q0) |
| Ket- / Messbits | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 | Kets / Messwerte (f1, d1, c1) |
| Dezimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Binär-Werte |
| q0: X(1,0)=(0,1) | 1 | q1, q2 sind (1,0) | |||||||
| q1: H(1,0) | 1/√2 | 1/√2 | Hadamard q1 ->1/√2(1,1) | ||||||
| CNOT q1->q2 | 1/√2 | 1/√2 | |||||||
| CNOT q0->q1 | 1/√2 | 1/√2 | |||||||
| q0: H | 1/2 | -1/2 | 1/2 | -1/2 | Hadamard q0 ->1/√2(1,-1) | ||||
| Messung (und Transfer) | 010 | 011 | 100 | 101 | Häufigkeit ca 25% | ||||
| q2: If d1==1 X | 1/2 | -1/2 | 1/2 | -1/2 | Bedingtes X-Gate | ||||
| q2: If c1==1 Z | 1/2 | 1/2 | 1/2 | 1/2 | Bedingtes Z-Gate | ||||
| Messung | 100 | 101 | 110 | 111 | q2 liefert immer 1 |
(Die leeren Felder stehen für 0, bzw. 0 Häufigkeit bei Messungszeilen.)
Wir haben damit am Ende nicht nur die konsistenten Messergebnisse, sondern auch den separierbaren 3-Qubit Zustand (0,1)⊗(1/√2,1/√2)⊗(1/√2,1/√2) mit q2 im Zustand (0,1). Auf ähnliche Weise kann man auch die Teleportation anderer q0-Zustände entwicklen.
Im nächsten Abschnitt werden wir uns mit einem Orakel beschäftigen und einem Algorithmus, der exemplarisch für den Beschleunigungseffekt des "Quanten-Parallelismus" steht. Doch zunächst die Ergänzung der Begriffstabelle und eine Pause.
Hier geht's dann weiter - stay tuned!
| Begriff englisch | Begriff deutsch | Bedeutung |
| Barrier | Barriere | Senkrechte, gestrichelte Linie in Composer-Circuit zur Abtrennung von Optimierungsbereichen. Hier nur als Strukturierung verwendet |
| Necessary condition | Notwendige Bedinung | In "wenn A, dann B": B ist notwendig für A. Zwangsläufige Folge |
| Sufficient condition | Hinreichende Bedingung | In "wenn A, dann B": A ist hinreichend für B |
| Reversibility method | Umkehr-Verfahren | Methode, das Vorliegen eines Qubit-Zustands zu prüfen unter Verwendung der prinzipiellen Umkehrbarkeit von Qubit-Operationen |
| No-Cloning Theorem | No-Cloning Theorem | Generelles Prinzip, dass Qubits nicht geklont werden können |
| State protocol | Zustandsprotokoll | Schematische Darstellung der Zustandsabfolge eines Qubit-Algorithmus |
| Quantum parallelism | Quanten-Parallelität | Bei Superpositionen wirkt ein Gate auf alle Komponenten der Basis-Zustände "parallel" |
Q13 Superdichte Codierung und Quanten-Kommunikation
Auf verschränkten Qubits lassen sich eine Reihe interessanter Effekte aufbauen - mit noch interessanteren Namen: Superdense Coding, Quanten-Kommunikation und Quanten-Teleportation sind sicher die spektakulärsten.
Superdense Coding bedeutet, dass man 2 Bit Information in einem Qubit "speichern" kann. Quanten-Kommunikation ermöglicht sichere Übertragung von 2 Bits durch ein Qubit und Quanten-Teleportation umgekehrt die Übertragung eines Qubit-Zustands durch 2 Bits. Wie das Qubit-algorithmisch geht und was das bedeutet, untersuchen wir in diesem Abschnitt. Falls der zu lang wird, lagern wir die Quanten-Teleportation auf den nächsten Blog aus.
Superdense Coding - Naiver Versuch und Bit-controlled Qubits
Wir werden die Idee des Superdense Coding zunächst auf einem Weg angehen, der naheliegend scheint, sich aber als Irrweg herausstellen wird. Wir können dabei jedoch eine interessante Möglichkeit der Qubit-Algorithmik kennen lernen: Das Zusammenspiel von klassischen Bits und Qubits: Bit-controlled Gates, manchmal auch Dependent Gates genannt.
Wir haben bereits kennen gelernt, wie man über den Zustand eines Qubit den eines anderen "steuern" kann: Controlled Gates. Es gibt bei Qubit-Algorithmen auch die Möglichkeit, Qubit Zustände durch klassiche Bits zu beeinflussen. Dabei wird, analog zum Controlled Gate, ein Qubit-Gate durch eine Bedingung gesteuert, in die die Bits eines Messergebnisses einbezogen werden. Wir nennen das hier Bit-controlled Gates.
Mit dem Composer wird ein Bit-controlled Gate dadurch erzeugt, dass das Gate auf einer Qubit-Linie mit dem If-Operator kombiniert wird. Das If-Symbol wird dazu einfach auf das Gate gezogen (Drag&Drop). Anschließend kann man das Gate editieren, d.h. die If-Bedingung nach Bedarf festlegen. Die If-Bedinung kann nur als Vergleich der gemessenen Bit-Kette (auf der c-Linie) mit einem Zahlenwert formuliert werden. Dabei werden die Bits der Messung als Binärzahl gewertet. (Mit der Qiskit-Bibliothek für Python sind das natürlich einfache If-Konstrukte, die sich auf die Mess-Bits beziehen.)
Hier ein Beispiel.
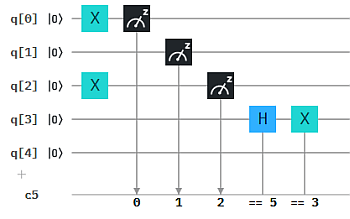Die Qubits q0, q1, q2 werden in die Zustände |1>, |0> bzw |1> versetzt und gemessen (1 shot) . Das ergibt die 3-Bit-Kette 00101, die Binärzahl für 5. Für Qubit q3 wird das Hadamard-Gate H angewendet, wenn das Messergebnis 5 ist. Wenn es 3 ist, wird dagegen X angewendet - also nicht im vorliegenden Fall. Bei allen anderen Messergebnissen passiert nichts mit q3.
Das Beispiel zeigt auch gleich einen einfachen Weg wie man Bits "von außen" in einen Circuit hineinbringen kann.
Die naheliegende Idee, zwei Bits in einem Qubit zu speichern, wäre, für die vier möglichen Kombinationen 00, 01, 10, 11 vier Superpositionen eines Qubit zu definieren, die durch Bit-gesteuerte Gatter erzeugt werden. Wir können zum Beispiel die Zwei-Bit-Ausdrücke durch die vier Zustände (1,0), (√2/3,√1/3), (√1/3,√2/3), (0,1) abbilden. (Das Wurzelzeichen bezieht sich auf den ganzen Bruch.) Diese liegen auf dem Einheitskreis im ersten Quadranten in Schritten von 30° Winkeln.
Das zu codierende Bit-Paar bringen wir wie beschrieben in den Circuit. Die dann anzusetzenden Bit-controlled Gates zeigt die Tabelle.
| Bit-Paar | 00 | 01 | 10 | 11 |
| Binär-Bedingung | 0 | 1 | 2 | 3 |
| Gate | ID | Ry(π/3) | Ry(2π/3) | X |
| Qubit-Zustand | (1,0) | (√2,√1)/√3 | (√1,√2)/√3 | (0,1) |
Für jedes vorgegebene Bit-Paar ergibt sich ein Mess-Ergebnis als Binärzahl, welche die Bedingung definiert, unter der das jeweilige Gate auf das "Speicher-Qubit" anzuwenden ist. Mit dem Composer lässt sich der Algorithmus wie folgt darstellen (Bit-Paar 11 ist als Input vorgegeben).
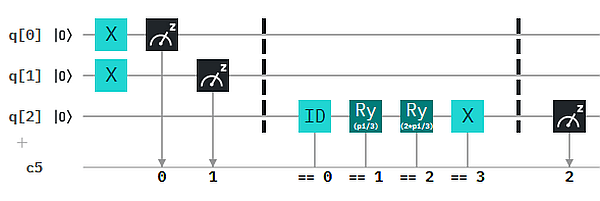Der erste Teil der "Partitur" setzt das zu codierende Bit-Paar als Zustand von q0 und q1. Der mittlere Teil versetzt je nach Wert der gemessenen klassischen Bits auf der c5-Linie das Qubit q3 in den entsprechenden Zustand.
Wir haben damit 2 Bits in einem Qubit codiert.
Wenn wir es recht überlegen, können wir auf diese Weise eigentlich auch 4, 8 oder beliebig viele Bits in einem Qubit codieren, denn es lassen sich mit Bit-controlled Ry-Gates (cRy) beliebig viele Qubit-Zustände herstellen. Das kling gut - zu gut, um wahr zu sein.
Das ist richtig für den Zustand des Qubits. Und solange wir mit dem Zustand weiter arbeiten im Qubit-Algorithmus, bleibt die Codierung auch erhalten. Wenn wir aber die Codierung rückgewinnen wollen - durch das Auslesen eines Speichers per Messung - bekommen wir lediglich eine 0 oder eine 1! Die Unterscheidung der 4 Zustände in Form von unterschiedlichen Häufigkeiten bekommen wir dagegen nur durch Wiederholungen, etwa 1024 shots. Die unterschiedlichen Zustände des Qubits präsentieren sich nur als Wahrscheinlichkeiten, und die kann man nur verifizieren durch viele Wiederholungen.
Das war der Irrweg. Besser geht's auf Basis von Verschränkung.
Superdichte Codierung - Verschränkung und Umkehrbarkeit
Der Irrweg war nicht ganz nutzlos. Wir müssen nur das manipulierte Qubit als Teil eines verschränkten Paares sehen. Statt den Algorithmus einfach aus Wikipedia abzuschreiben (wenn man es dort überhaupt versteht), versuchen wir mittels der uns schon bekannten algorithmischen Bausteine den Algorithmus selbst zu konstruieren. Wer keine Lust dazu hat, kann diesen Teil überspringen und gleich mit der Zusammenfassung des Superdense Coding Verfahrens weiter machen.
Eine wichtige Eigenschaft von Qubit-Gates ist noch gesondert hervorzuheben, obwohl sie uns in vielen Beispielen seit der ZBIT-Box schon begegnet ist: Die Reversibilität oder Umkehrbarkeit von Gates und Gate-Kombinationen. In der Qubit-Welt sind außer der Messung, bzw außer Interaktionen mit klassischen Bits, die Operationen umkehrbar. Für jedes Gate und jede Gate-Folge gibt es die Möglichkeit, den Ausgangszustand wieder herzustellen.
Wir wissen z.B. schon, dass zur Umkehrung von X und H die Gates selbst verwendet werden können. Anders ausgedrückt: X---X und H---H ergeben das Gleiche wie das ID-Gate, das den Qubit-Zustand erst gar nicht verändert. Für Drehungen mit Ry gibt es für jeden Drehwinkel einen komplementären Winkel, so dass z.B. Ry(2π/3) durch Ry(-2π/3) wieder aufgehoben wird. Wer Lust hat, kann sich alle bisher erwähnten 1-Qubit Gates noch einmal daraufhin anschauen - auch an Hand der Berechnungsformeln (s. Q10) - oder mit Hilfe von Composer-Tests. Auch Gate-Abfolgen mit controlled Gates wie CNOT (cX) und Tofoli (ccX) lassen sich umkehren. Darunter fällt auch unsere Standard-Verschänkung, Circuit 7 aus Q10, die aus H und CNOT gebildet wird. Die Umkehrung besteht aus beiden Gates in umgekehrter Reihenfolge und löst die Verschränkung wieder auf.
Nun zur Codierung: Wir brauchen ein verschränktes Qubit Paar, statt nur ein Qubit wie oben. Wir erzeugen das mittels H und CNOT aus den Standard-Ausgangszuständen von q0 und q1. Wenn wir nun die 2-Bit Information 00 "codieren" wollten, müssen wir erreichen, dass sich am Ende bei der Messung auch immer (zu 100%) 00 ergbit. Dieses Ergebnis 00 erfolgt aus der Messung von zwei Qubits im Ausgangszustand. D.h. wir codieren 00, indem wir nach der Verschränkung diese wieder umkehren, also dem H---CNOT ein CNOT---H folgen lassen. Wenn wir wollen, können wir zwischen diesen beiden Circuit-Teilen ein ID-Gate auf die q0-Linie setzen. Damit kann man sagen, das ID-Gate codiert die zwei Bits 00.
Damit hat man die algorithmische Idee für die Codierung von 2 Bits: wir prüfen, welche 2 Bits "am Ende herauskommen", wenn wir statt ID andere Gates auf die q0-Linie setzen. Das kann man ausprobieren, oder auch errechnen, wie wir es in Q10 getan haben. Tatsächlich finden wir heraus, dass Z, X und die Kombination X---Z die drei anderen 2-Bit-Ergebnisse liefern.
Der Algorithmus in Worten zusammengefasst:
- Es wird ein Qubit Paar in den verschränkten Zustand 1/√2(|00>+|11>) versetzt.
- Ein Qubit wird für die vorgegbenen 2 Bits mit einem passenden Gate "codiert", das andere Qubit bleibt unberührt.
- Um die codierte 2-Bit Information wieder abzurufen, erfolgt eine Gate-Kombination, die unabhängig ist von der in dem einen Qubit "gespeicherten" Information. Danach werden beide Qubits gemessen (1 shot).
Im Composer sieht der Algorithmus so aus: (Wir lassen den Teil der Bit-Paar-Bereitstellung weg. Der wäre wie oben davor zu schalten.)
Im ersten Teil wird der schon aus Q9 bekannte verschränkte Zustand zwischen q0 und q1 hergestellt. Im mittleren Teil erfolgt die Codierung auf q0. Dabei steht für jedes der vier 2-Bit Paare eine bestimmte Gate-Kombination (s. folgende Tabelle). Damit ist das Bit-Paar in q0 codiert, ähnlich wie beim ersten Versuch.
Da q0 Teil eines verschränkten Systems ist, kann mit den Gates und Messungen im rechten Teil die Information bei Bedarf wieder ausgelesen werden. Wie schon erklärt, ist die Gate-Kombination die Umkehrung der Gates im Verschränkungsteil.
Mit 1-shot Durchläufen auf dem QC-Simulator können wir diesen Qubit-Algorithmus überprüfen. Im Beispiel ist das Bitpaar 01 codiert. Zur Codierung der 4 möglichen 2-Bit Paare verwendet man im Composer folgende Gates auf q0:
| Bit-Paar | 00 | 01 | 10 | 11 |
| Gates auf q0 | ID | Z | X | X --- Z |
Dabei bedeutet X --- Z, dass hier X und Z nacheinander angewendet werden. Natürlich kann man den Effekt auch "rechnerisch" mittels der Zustansabfolge nachweisen.
Wer Lust hat, kann versuchen, diesen Circuit so zu erweitern, dass man, wie im ersten Versuch, den "Bit-Input" über zwei zusätzliche Qubits und Bit-controlled Gates implementiert. Entweder als Skizze oder im Composer, wenn der Zugang zu IBM Q Experience besteht.
Wenn man diesen Qubit-Algorithmus zum Speichern (und wieder Auslesen) von 2 Bit kritisch betrachtet, wird klar, das eigentlich nicht viel gewonnen ist. Man benötigt zwei Qubits, in verschränktem Zustand, um eine 2-Bit Information "abzulegen" und gelegentlich wieder auszulesen. Um weitere 2 Bit zu speichern, benötigt man wieder zwei verschränkte Qubits. Der subtile Unterschied liegt lediglich darin, dass nur das eine Qubit die 2 Bit Information per Gates "aufgeprägt" bekommt, das andere in der Verschränkung unberührt bleibt. Trotzdem gibt es bei der Messung "seinen Anteil" der 2-Bit Information determiniert aus, hat sich also ggf. verändert. (Mit der Mehr-Qubit GHZ-Verschränkung sieht der Effekt aber schon wieder anders aus. Darauf kommen wir am Ende des Abschnitts Qubit-Kommunikation zurück.)
Plausibler wird der Superdense-Effekt allerdings bei einem anderen Einsatz des Algorithmus, nämlich zur Kommunikation.
Superdichte Codierung - Qubit-Kommunikation
Superdense Coding kann man einsetzen, um z.B. 2 Bit Information mittels eines Qubits zu übertragen, d.h. den Übertragungsaufwand gegenüber bit-weiser Kommunikation zu halbieren.
Auch wenn wir in dieser Blog-Serie die physikalischen Hintergründe vermeiden, muss man sich für das Folgende klar machen, dass es dem Großen Experimentator tatsächlich gelungen ist, verschränkte Qubits einzeln und über getrennte Wege an verschiedene Empfangsstellen zu schicken. Ähnlich, oder sogar mit den gleichen Mitteln, wie wir die klassische Datenübertragung (Internet) kennen. Das geht inzwischen über Hunderte von Kilometern. Wenn also von Qubit Senden die Rede ist, ist das nicht nur eine Fiktion, sondern praktisch realisierbar.
Die Interpretation des Superdense Coding Algorithmus, oben, als Kommunikationsmethode zwischen zwei Teilnehmern, üblicherweise Alice und Bob, ist wie folgt: Alice möchte Bob eine Nachricht (2 Bit) schicken,
- Bob erzeugt eine Verschränkung von zwei Qubits im Ausgangszustand.
- Eines der Qubits schickt er an Alice, das andere behält er.
- ------ Erste Trennlinie ------
- Alice möchte 2 Bits an Bob übermitteln. Dazu codiert sie mittels der passenden Gates (s.o.) die 2 Bits in ihr Qubit.
- Anschließend sendet sie ihr codiertes Qubit an Bob.
- ------ Zweite Trennlinie ------
- Bob wendet die Gates CNOT und H auf die Verschränkung an
- und misst Alice's und sein Qubit.
- Bob erhält damit die Nachricht von Alice.
Obwohl hier auch zwei Qubits im Spiel sind, wird nur das eine für die Kommunikation gebraucht. Alice "codiert" ihre Nachricht an Bob durch Anwendung von Gates auf dieses eine Qubit und schickt es zurück. Das andere Qubit tut nichts. Es ist lediglich Basis für die Verschränkung. Man kann das ganze wiederholen für eine beliebige binär codierte Nachricht, jeweils 2 Bit auf einmal, z.B. zur Übermittlung eines geheimen Schlüssels.
Ohne das hier näher zu erörtern, weist die Qubit-Kommunikation auch gewisse Sicherheitsmerkmale auf. Zum einen kann Alice's Information nicht gelesen werden ohne das zweite Qubit der Verschränkung. Zum anderen kann die Nachricht nicht "abgefangen" werden, ohne dass der Verschränkungszustand gestört wird.
Qubit-Kommunikation mit Mehr-Qubit GHZ Verschränkung
Das Kommunikationsverfahren mit zwei verschränkten Qubits lässt sich auf mehrere Qubit-Systeme erweitern. Wir kennen bereits aus Q11 die GHZ-Verschränkung, die eine konsistente Erweiterung unserer 2-Qubit-Verschränkung auf 3 und mehr Qubits ermöglicht. Damit können wir das Verfahren der 2-Bit Übertragung auf mehrere Bit ausdehnen. D.h. wir könnten statt 4 Zwei-Bit-Kombinationen mit einem verschränkten Qubit-Paar mehr Information übertragen, indem Alice z.B. alle außer einem Qubit bekommt und codiert zurück sendet. Wie die Tabelle zeigt,
| GHZ Qubits | 2 | 3 | 4 | 5 |
| # Alice's Qubits | 1 | 2 | 3 | 4 |
| # Bit-Ketten | 4 | 8 | 16 | 32 |
kann Alice auf zwei Qubits die 8 Bitketten 000, ... 111 unterbringen. Die Gate-Kombinationen auf den beiden Qubit-Linien sind allerdings nicht so einfach wie oben. Wir haben 4*4 Gate-Kombinationen, also 16 Möglichkeiten, die 8 3-Bit-Ketten zu codieren. Die Tabelle zeigt, wie das geht (Ergebnisse der 16 Circuits).
| ID | Z | X | X---Z | q0 | |
| ID | 000 | 001 | 010 | 011 | |
| Z | 001 | 000 | 011 | 010 | |
| X | 110 | 111 | 100 | 101 | |
| X---Z | 111 | 110 | 101 | 100 | |
| q1 |
Die Composer-Grafik zeigt als Beispiel einen Qubit-Circuit mit 2 Qubits, die Alice mit q0: Z und q1: XZ codiert hat. Bob bekommt damit die 110.
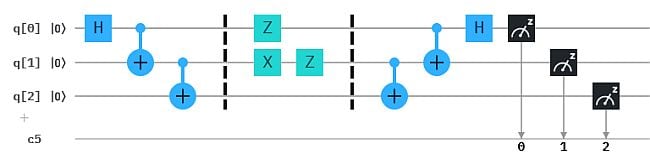Wie man an der Tabelle sieht, gibt es immer zwei Gate-Kombinationen, die die gleiche 3-Bit-Kette codieren. Alice kann aber alle bereits dadurch abdecken, dass sie für q0 die gleichen 4 Gate-Kombinationen wie oben wählt und für q1 entweder ID oder X.
Der Verdichtungsfaktor, das Verhältnis Bit-Information zur Anzahl zu codierender Qubits, vergrößert sich mit zunehmender Qubit-Zahl nicht-linear: bei 1 und 2 Qubits ist er 4, bei 3 bereits 16/3 und bei 4 immerhin schon 8.
Hier noch zwei Beispiele für eine 16-zu-3 Codierung: X auf q0, q1, q2 codiert 1000; mit Z statt X auf q1 wird 1111 codiert. Wer Lust hat, kann das mit dem Composer und der 4-Qubit-Verschränkung überprüfen.
Von dieser Stelle aus lassen sich vielfältige Ideen, Experimente und Untersuchungen entwickeln. Zum Beispiel könnten die Qubits an verschiedene Empfänger geschickt werden. Es sei dem eigenem Interesse überlassen, Szenarien hierzu zu überlegen.
Wir legen hier wieder eine Pause ein und vertagen das Thema Quanten-Teleportation auf den nächsten Blog. Eine Kaffepause und etwas Bewegung tun jetzt gut.
Und hier geht es weiter - stay tuned!
Neue Begriffe in diesem Abschnitt:
| Begriff englisch | Begriff deutsch | Bedeutung |
| Superdense Coding | Superdichte Codierung | Codierung von 2-Bit Information in einem Qubit |
| Quantum Communication | Quanten-Kommunikation | Übertragung von (superdichter) Bit-Information durch ein Quantensystem |
| Quantum Teleportation | Quanten-Teleportation | Übertragung eines Qubit-Zustands auf ein anderes Qubit |
| Dependent Gate | Bit-controlled Gatter | Gate, das abhängig von klassichen Bits auf den Qubit-Zustand wirkt |
| If Operator | If-Operator | |
| Reversibility | Reversibilität | Grundsätzliche Umkehrbarkeit von Qubit-Operationen |
| Compression Factor | Verdichtungsfaktor | Verhältnis von Bit-Information zur Anzahl verwendeter Qubits. Z.B. 2 Qubits für 8 3-Bit-Ketten: Faktor 4 |
Q12 Ein echter Quanten-Würfel in 3 Qubits
Ein normaler Spiel-Würfel hat sechs Flächen mit Punkten (Augen) von 1 bis 6. Bei Games oder Simulation von Zufallsvorgängen werden Würfel, oder allgemein Zufallszahlen, durch trickige mathematische Verfahren imitiert. Pseudo-Zufallszahlen heißen sie deshalb, weil sie nicht echt zufällig sind, sondern das Ergebnis einer festgelegten Berechnungsformel. Die ist für uns nur so kompliziert, dass wir das Ergebnis nicht wirklich "verstehen" oder vorhersagen können. Also akzeptieren wir das als "Zufall", obwohl es genau berechnet ist.
Der Spiel-Würfel ist echt. Da gibt es keine Funktion, nach der wir das Ergebnis eines Wurfs berechnen könnten. Wirklich nicht? Nun ja, prinzipiell doch, denn er gehorcht ja klaren physikalischen Gesetzen in dem, wie er sich dreht, wie er fällt, wie er rollt, wie er kippt. Aber auch diese alle zusammen sind wieder so kompliziert, dass wir gut darauf vertrauen können, dass er ein "neutrales" Zufallsergebnis liefert.
Der Quanten-Würfel ist nicht nur echt, sondern es ist sogar prinzipiell nicht möglich das Ergebnis voraus zu berechnen. Prinzipiell heißt hier, nach den Prinzipien der Quantenphysik. Zugegeben, es ist schwer, das zu glauben - aber man kann das sogar beweisen, d.h. die Physiker können das.
Wenn wir also einen Qubit-Algorithmus entwerfen können, der Würfelergebnisse durch Messung liefert, und wenn wir den auf einem echten Quantencomputer laufen lassen würden, hätten wir einen wirklich echten Würfel.
Ein Würfel-Qubit-Algorithmus
Einen einfachen Zufallsgenerator, der wie beim Münzwurf 0 oder 1 liefert, kennen wir schon: Wir versetzen ein Qubit in den Zustand |+> = H|0> und messen. Das ergibt ein Bit. Wir können das dreimal tun und erhalten ein 3-Bit-Ergebnis, von 000 bis 111. Das sind allerdings 8 mögliche Ergebnisse, für den Würfel brauchen wir genau 6 mit gleicher Wahrscheinlichkeit 1/6.
In der Zahl sechs liegt hier unser kleines Problem. Mit 2 Qubits können wir bis zu 4 verschiedene 2-Qubit-Messergebnisse erzielen. Wir kennen bereits Circuits, die ein, zwei, oder vier 2-Bit Ergebnisse liefern. Wir werden sehen, dass man auch Circuits konstruieren kann, die drei davon liefern mit gleicher Wahrscheinlichkeit. Aber auch das ist schon nicht so einfach.
Wir benötigen sechs, also brauchen wir 3 Qubits. Es ist einfach damit 1, 2, 4 oder 8 3-Bit Messergebnisse mit Häufigkeit größer Null zu erzielen. Aber sechs?
Wir versuchen folgende Methode:
Wir zerlegen das Problem in zwei Teilprobleme 6 = 3*2 : (a) die Konstruktion eines Circuits, der drei gleichwahrscheinliche Messergebnisse liefert, (b) eine Erweiterung, die den Endzustand von (a) noch in zwei gleichwahrscheinliche aufteilt.
Während (b), gefühlt, einfach erscheint - wir kennen ja die Wirkung von H - ist (a) etwas komplizierter. Aber auch hier teilen wir wieder auf: Wir brauchen einen Cicruit, der zwei Ergebnisse im Verhältnis 1/3 : 2/3 liefert, und versuchen dann, die 2/3 wieder in zwei gleichwahrscheinliche Ergebnisse "aufzuteilen".
Klingt, als könnte das gehen - aber wie? Zwei Ergebnisse mit unterscheidlichen Häufigkeiten hatten wir schon in Q8 für 1 Qubit erzeugt, durch Drehung mit Ry. (Das Schöne an den Qubit-Algorithmen ist, dass wir unsere Ideen - auch schrittweise - immer gleich überprüfen können mit dem IBM Composer und qasm-Simulator!) Also probieren wir mal:
Der Zustand auf dem Einheitskreis mit den Koordinaten (1/√3, 2/√3) liefert das gewünschte Ergebnis: (1,0) mit 1/3 und (0,1) mit 2/3 Wahrscheinlichkeit. Wie kommen wir vom Ausgangszustand (1,0) dahin? Es gibt verschiedene Wege. Der einfachste ist mittels einer Drehung um den passenden Winkel. Hier muss man den Taschenrechner bemühen und z.B. die arccos-Funktion mit 1/√3 aufrufen. Der Drehwinkel ist damit 0.955317. Wenn wir diesen mit Ry realisieren wollen, müssen wir wieder daran denken, dass der Ry-Winkel immer als das Doppelte vom Winkel im Koordinatensystem genommen werden muß (s. Q8). Wir komponieren also
|0> ---> Ry(2*0.955317) ---> M (Messung) ---> 000 und 001 zu 1/3 bzw 2/3
Der Simulationslauf bestätigt das!
Nun müssten wir 001 noch "aufteilen" in zwei Ergebnisse mit je 1/2 Wahrscheinlichkeit. Das wird trickig. Die 2/3 kommen aus der Komponente |1> des q0-Zustands. Die können wir mit einem geeigneten controlled Gate auf ein zweites Qubit "übertragen" werden. Sie müssen aber auf die Zustände |0> und |1> von q1 1:1 aufgeteilt werden. Damit würde der |1>-Anteil von q0 kombiniert werden mit den beiden Basiszuständen von q1. Gleichzeitig darf aber der |0>-Anteil von q0 nicht mit einem |1>-Anteil von q1 kombiniert werden, denn sonst hätten wir wieder 4 Ergebnisse. Was bietet sich an? Das controlled Hadamard-Gate! Das lässt zum Teil den q1 Ausgangszustand |0> unberührt und zum anderen Teil "dreht" es diesen auf 1/√2(|0>+|1>). Hier ist das Composer-Diagramm dazu.
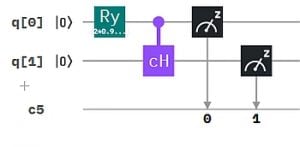Die Läufe auf dem Simulator liefern das gewünschte Ergebnis: 00, 01 und 11 mit Häufigkeiten z.B. 31.25%, 34.18% und 34.57%. Wie oben erwähnt haben wir hiermit auch ein Beispiel für ein 2-Qubit-System, das 3 der vier möglichen Messergebnisse aufweist.
Wir wollten aber einen Würfel konstruieren. Für Schritt (b) brauchen wir nur ein weiteres Qubit in eine 1:1 Superposition zu bringen. Dann bekommen die 3 2-Qubit Ergebnisse von (a) jeweils eine 0 oder 1 "dazugeschaltet". Das geht am einfachsten mit dem Hadamard-Gate. Das Composer-Diagramm und ein Ergebnis-Histogramm von 1024 Shots:
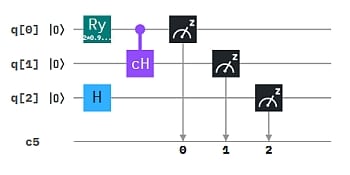
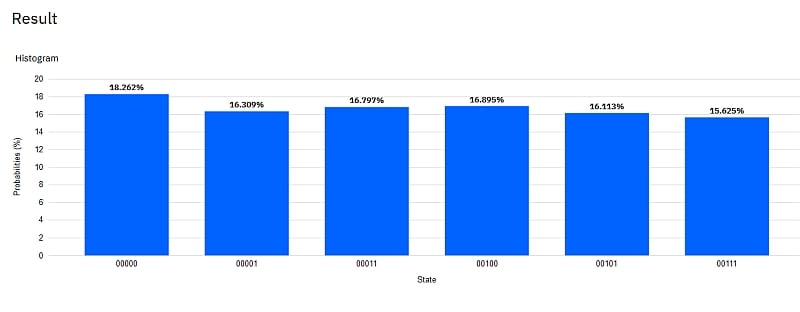Das Ergebnis-Histogramm zeigt die 6 "Würfel-Ergebnisse" mit etwa gleicher Häufigkeit. Natürlich sind die Bit-Ketten unter den Säulen nicht als Binärzahlen zu nehmen. Eine Interpretation als Augenzahl ist allerdings simpel. (Wir werden an anderer Stelle ein Würfelspiel in Form eines Python Programms unter Verwendung des IBM QC-Package Qiskit zeigen.) Wir können z.B. folgende Übersetzung festlegen
| Qubit-Ergebnis | 00000 | 00001 | 00011 | 00100 | 00101 | 00111 |
| Augenzahl | 2 | 1 | 3 | 4 | 5 | 6 |
Dann sind immerhin die mittleren vier Augenzahlen in den Bitketten als Binärzahl repräsentiert.
Die W-State Verschränkung
Die Idee für den obigen, letztlich doch recht einfachen Qubit-Algorithmus für einen Würfel, geht auf einen Artikel zurück, in dem P. Decoodt in einem GitHub Beitrag von 2019 (Link) die Erzeugung sog. verschränkter W-Zustände beschreibt.
W-Zustände können beliebig viele Qubits in der Weise verschränken, dass jedes darin nur einmal mit ihrem Basiszustand |1> vertreten sind. Also etwa
1/√2(|01>+|10>) für n=2 Qubits
1/√3(|001>+|010>+|100> für n=3, und
1/√n(|00...01>+|00...10>+....+|10...00>) allgemein.
Für n=3 sieht man, dass der W-Zustand bei Messung genau 3 Ergebnisse mit gleicher Wahrscheinlichkeit liefert. Daher ist er ein guter Kandidat für den Schritt (a) eines Würfel-Algorithmus. Es gibt in dem erwähnten Beitrag einen sehr eleganten Algorithmus, bzw. ein algorithmisches Schema, nach dem die W-Zustände für n Qubits generiert werden können. Für n=3 und in Composer-Darstellung übersetzt, sieht das wie folgt aus:
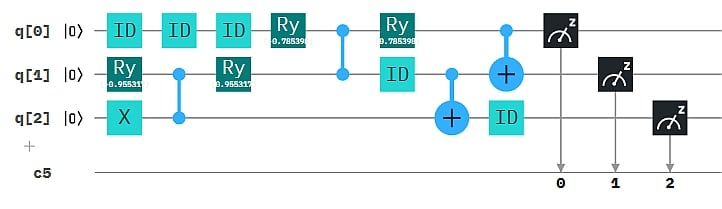
(Die ID Gates kann man sich weg denken. Sie stehen dort nur, damit die elegante Struktur des Algorithmus deutlich wird. Der Composer schiebt ansonsten alles zusammen, was die Ausführungsabfolge nicht beeinträchtigt.) Was man hier an der Grafik nicht erkennt, ist, dass die cZ-Gates in diesem Algorithus "von unten nach oben" weisen. D.h. die Control-Qubits sind q2 und q1, die Target-Qubits q1 bzw q0. Die "Richtung" lässt sich im cZ-Gate editieren.
Der Algorithmus liefert drei mögliche Messergebnisse: 001, 010 und 100. Und die zusätzliche Idee für einen echten Würfel besteht damit nur noch darin, diese drei zu gleichen Anteilen "aufzuspalten". Da kommt das Hadamard-Gate gerade recht, das am Ende der q2-Lebenslinie hinzugefügt wird. In der Abbildung also nach dem ID-Gate und vor den Messoperatoren.
Insgesamt ist der W-Zustand Algorithmus als Teil des Würfel-Algorithmus aber recht komplex, daher lohnt es, sich die einzelnen Schritte des genauer anzusehen. Zunächst stellt man fest, dass die beiden CNOT Gates nicht nötig sind, um auf genau drei verschiedene Messergebnisse zu kommen. Auch hier ist es gute Praxis, die Messpunkte im Composer einfach zu verschieben, um zu überprüfen, was der bis zu einer bestimmten Stelle im Algorithmus entwickelte Zustand ergibt. Setzt man die Messpunkte z.B. hinter das zweite Ry-Gate auf der q0-Linie, bekommt man zwei Messergebnisse im Häufigkeitsverhältnis 1/3 : 2/3. (Allerdings nicht den W-Zustand. Der ist aber auch für den Würfel unerheblich.)
Die nächste Vereinfachnung ergibt sich, wenn man bedenkt, dass das X anfangs der q2-Linie nur den q2-Zustand so umstellt, dass das controlled Z (cZ, senkrechte Linie mit zwei Punkten) immer greift. Man kann also das X und das cZ weglassen, wenn man dafür ein Z an diese Stelle auf der q1-Linie platziert. Das bedeutet aber, dass sich der Zustand von q1 zunächst unabhängig entwickelt: Eine Drehung in negative Richtung um einen bestimmten Winkel θ, eine Spiegelung an der x-Achse (Wirkung des Z-Gates), was insgesamt einer Drehung des Ausgangszustands um θ in positiver Richtung (in den 1. Quadranten des Koordinatensystems) entspricht. Anschließend erfolgt eine Drehung noch einmal um θ, so dass wir insgesamt bei einem Winkel von 2*θ ankommen. Daher kann man das ganze Geschehen auch abkürzen, indem man statt dessen für q1 nur eine Drehung (Ry) um 2*θ in positiver Richtung als Gate ansetzt. Nun muss man θ so festlegen, dass der Zustand die zwei Messergebnisse im Verhältnis 1/3 : 2/3 liefert. Dieser Winkel ist im W-Algorithmus bereits bestimmt (0.955317 oder arccos(1/√3) ), man kann ihn also übernehmen. Mit dem Composer kann man das Ergebnis unmittelbar überprüfen.
Es bleibt die Überlegung für das Zusammenspiel zwischen q1 und q0. Der Zustand von q0 wird zunächst ebenfalls (per Drehung) verändert. Dann greift das cZ: die Wirkung des Z-Gates beschränkt sich auf den |1> Anteil des q1-Zustands. Mit diesem Anteil wird der q0-Zustand gespiegelt und anschließend noch einmal um φ in positiver Richtung gedreht. Dieser "Anteil" ist damit in einem Zustand, der im Koordinatensystem mit dem Winkel 2*φ auf dem Einheitskreis liegt. Der andere Anteil des q0-Zustands wird lediglich wieder "zurück gedreht" auf den Ausgangszustand |0>. Der Winkel φ muss so bestimmt werden, dass der zugehörige Zustand zur Hälfte aus |0> und zur Hälfte aus |1> besteht. Das kann man aber insgesamt auch erreichen, indem man die Drehungen mit dem Ry-Gate und das cZ ersetzt durch ein einfaches controlled H (cH) "von q1 nach q0". Genau das haben wir oben getan, was uns zu dem schlichten Würfel-Algorithmus oben geführt hat. (Allerdings haben wir dort q0 und q1 vertauscht.)
Wir lernen daraus auch eine Methode des Qubit-algorithmischen Denkens: Effekte von Gates zu verstehen und parallel mit Hilfe des einfachen grafischen Composer Tools zu überprüfen, indem man systematisch Messpunkte setzt bzw. verschiebt. Verschieben eignet sich insbesondere für die Analyse von Qubit-Algorithmen, das systematische Setzen beim Entwurf von Qubit-Algorithmen.
Die Erläuterung der Wirkung von cZ oder auch des cH zwischen q1 und q0 macht auch deutlich, warum man zu der Deutung neigt, dass ein Qubit "in zwei Zuständen gleichzeitig" sein kann - vereinfacht zu: "Ein Qubit kann gleichzeitig 0 und 1 sein". Mittels controlled Gates kann ein Zustand, der eine Superposition (i.e. Linearkombination) darstellt, eingesetzt werden, um ein anderes Qubit auf zwei unterschiedlichen "Wegen" weiter zu entwickeln. Es ist, als würde man gleichzeitig zwei "Schicksale" des gleichen Qubit verfolgen. Von da aus ist es nicht weit bis zu der phantastischen Vorstellung von gleichzeitig existierenden Parallelwelten. Wir kommen darauf in einem späteren Blog noch einmal zurück.
Der rekursive W-State Algorithmus hat interessantes Potenzial über die Würfel-Implementierung hinaus. Wir können damit im Prinzip jede Anzahl von Messergebnissen realisieren. Z.B. mit n=5 Verteilungen über 5 Bitketten der Länge 5. Und mit "Aufspaltungen" wie oben in Schritt (b) bei n=3 auch gerade Vielfache davon.
Im nächsten Abschnitt versuchen wir uns am Super Dense Coding, bei dem man mit n Qubits 2n Bits an Information übertragen kann. Ebenfalls eine Quelle vieler Mythen.
Vorher aber eine Spiel-Pause - mit dem Quantenwürfel. Stay tuned!
Tabllen-Ergänzung
| Begriff englisch | Begriff deutsch | Bedeutung |
| Pseudo random numbers | Pseudo-Zufallszahlen | Mit einer determinierten Rechenvorschrift erzeugte Zahlen, die uns "zufällig" erscheinen |
| Histogram | Histogramm | Säulen-Darstellung von Zahlenwerten, z.B. Häufigkeiten von Ereignissen |
| W State | W-Zustand | Verschränkter n-Qubit Zustand besonderer Struktur |
| Target Qubit | Ziel-Qubit | Andere Bezeichnung für das Controlled Qubit bei einem Controlled Gate |
| Algorithmic schema | Algorithmisches Schema | Allgemeine Struktur von Algorithmen, die mehreren Algorithmen zugrunde liegen kann. |
| ID Gates | ID-Gatter | Wirkungsloses Gatter, das i.w. zu besseren Strukturierung von Composer Grafiken verwendet werden kann. Auch für zeitliche Taktung. |
| Qubit Algorithmic Thinking | Qubit-algorithmisches Denken | Verstehen, Analysieren und Entwerfen von Qubit-Algorithmen als speziellem Algorithmus-Typ |
Q11 3-Qubit Circus
So sieht ein Circuit mit 3 Qubits im IBM Q Composer aus.
3-Qubit Zustände
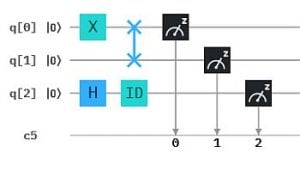Wir haben hier auch gleich einmal das Swap-Gate zwischen q0 und q1 eingesetzt und das ID-Gate.
Was wird das Messergebnis sein? Klar, q0 liefert 0, q1 liefert 1, beides jeweils zu 100%. Aber H (mit oder ohne ID) liefert für q2 je 50% 0 und 1. D.h. als 3-Qubit Messergebnis können wir 010 und 110 zu je 50% erwarten. (Der Lauf auf dem Simulator bestätigt die Erwartung.)
Erstaunlich - dies ist die Analyse eines Mini-Qubit-Algorithmus mit immerhin 3 Qubits, die wir allein aus der Interpretation der Gates abgeleitet haben. Das war übrigens auch schon bei den vergangenen Circuit-Beispielen der Fall. Andererseits kann man den Algorithmus auch "formelmäßig berechnen", indem man, ausgehend vom Anfangszustand der Qubtis, die Abfolge der Zustände über die Gate-Formeln berechnet. Das haben wir ernsthaft schon in Q10 begonnen.
Nun zu den 3-Qubit-Zuständen. Mit dem allgemeinden Zustand (r,s) für q2 rechnen wir analog zum 2-Qubit-Zustand:
(r,s) ⊗ ((u,v)⊗(x,y)) = (r,s) ⊗ (ux, uy, vx, vy) = (rux, ruy, rvx, rvy, sux, suy, svx, svy)
Das Resultat ist ein 8-dimensionalen "Punkt". Wieder ist die Summe der Quadrate der Koordinaten =1. Und alle 8-Koordinaten-Punkte, die diese Bedingung erfüllen sind wieder zulässige 3-Qubit-Zustände. Die Berechnung des 3-Qubit-Zustands aus den Zuständen der einzelnen Qubits ist assoziativ aber nicht kommutativ. D.h. es ist zwar egal, ob erst (r,s)⊗(u,v) gerechnet wird oder erst (u,v)⊗(x,y), aber es ist nicht egal, ob man die Reihenfolge der Qubit-Zustände vertauscht: (r,s)⊗(u,v) ist nicht das Gleiche wie (u,v)⊗(r,s). Nur zur Warnung!
Verfolgen wir die Zustände im obigen Beispiel:
q0 (1,0) ---> X ---> (0,1) ---> Swap ----> (1,0) = (x,y)
q1 (1,0) ---------------------> Swap ----> (0,1) = (u,v)
q3 (1,0) ---> H ---> 1/√2(1,1) ---> ID --->1/√2(1,1) = (r,s)
Damit wird der 3-Qubit-Zustand zum Zeitpunkt der Messung
1/√2(1,1) ⊗ (0,1) ⊗ (1,0) = (0, 0, 1/√2, 0, 0, 0, 1/√2, 0)
Man macht sich hier zunutze, dass der 3-Qubit-Zustand separabel ist; denn er wird ja aus drei 1-Qubit-Zuständen zusammen gesetzt.
Messung und Kets
Wie passt das zur Messung? Dazu müssen wir den M-Operator auf 3-Qubit-Zustände erweitern. Ein solcher Zustand (a0, a1, a2, a3, a4, a5, a6, a7) lässt sich mit 3-Kets schreiben als a0|000>+a1|001>+a2|010>+a3|011>+a4|100>+a5|101>+a6|110>+a7|111>
Dabei sind die 3-Kets wieder die Abkürzungen für |0>⊗|0>⊗|0> = |000> usw. Allgemein gilt die Schreibweise |ijk> = |i>⊗|j>⊗|k>.
Und da wir gerade dabei sind, stellen wir fest, dass die 0-1-Folgen in den 3-Kets genau die Dezimalzahlen 0, 1, 2, ..., 7 ergeben, wenn man sie als Binärzahlen interpretiert. Und wenn wir die Koordinaten a0, ... a7 so durchnummerieren wie in der Ket-Summe, dann passen die gerade zu den Kets als Dezimalzahlen.
Damit kann man nun den Operator M so festlegen - und das gilt für beliebige Anzahlen von Qubits:
M(a0, a1, a2, a3, a4, a5, a6, a7) = (|a0|², |a1|², |a2|², |a3|², |a4|², |a5²|, |a6|², |a7|²)
und dabei bedeutet z.B. |a5|² die Wahrscheinlichkeit dafür, dass wir als Messergebnis 101, die Binärzahl für 5, bekommen. Und ja, man schreibt dann natürlich auch manchmal den Ket mit der Dezimalzahl statt der Bitkette: |101> = |5>. Allgemein:
|i>⊗|j>⊗|k>=|ijk>=|d>, wobei d=i*2²+j*2¹+k*2°
Dabei den Durchblick zu behalten, ist schon eine ziemliche Herausforderung. Aber es musste mal gesagt werden - auch wenn wir möglichst bei der Koordinatendarstellung von Zuständen bleiben.
Zurück zur Messung im Beispiel oben: der M-Operator angewendet auf den 3-Qubit-Zustand
1/√2(1,1) ⊗ (0,1) ⊗ (1,0) = (0, 0, 1/√2, 0, 0, 0, 1/√2, 0)
ergibt die Wahrscheinlichkeiten (0,0,1/2,0,0,0,1/2,0). D.h. nur 010 und 110 kommen bei Messungen vor.
Man muss darauf achten, dass man Zustände in Koordinatenschreibweise und Messwahrscheinlichkeiten sachlich und sprachlich voneinender unterscheidet. Insofern ist die Ket-Schreibweise wiederum hilfreich, weil sid ganz anders "aussieht" als die Liste der Wahrscheinlichkeiten, die M liefert.
Tofoli Gate
Das Tofoli-Gate ist ein CCNOT Gate, d.h. q0 und q1 steuern q2: wenn beide im Zustand (0,1) sind (also |1> als Ket), wird der Zustand von q2 umgedreht, sonst bleibt er unverändert. Mit (x,y), (u,v) und (r,s) als Zustände von q0, q1 bzw. q2, überführt das Tofoli-Gate den 3-Qubit-Zustand
(r,s) ⊗ (u,v)⊗(x,y) = (rux, ruy, rvx, rvy, sux, suy, svx, svy)
---> CCNOT
---> (rux, ruy, rvx, svy, sux, suy, svx, rvy)
d.h. die 4. und 8. Koordinate werden vertauscht. Das ist einfach zu verstehen: v und y sind die Anteile von (0,1) (oder |1>) in den beiden Control-Qubits q0 und q1. Kommen beide zusammen in einer Koordinate des 3-Qubit-Zustands vor, wechselt q2 die Zustandskoordinaten. Damit wird in der 4. Koordinate rvy zu svy und umgekehrt in der 8. Koordinate.
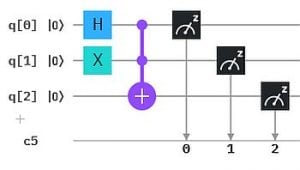Ein Beispiel-Circuit mit Tofoli-Gate (CCNOT). Es liefert 010 und 111 mit Wahrscheinlichkeit 1/2. Eine gute Übung, das Ergebnis über die Zustandsentwicklung nachzuvollziehen.
Logische Gates
Wenn wir das Tofoli-Gate (auch CCNOT oder ccX genannt) mit den Controlled Gates in den 2-Qubit-Circuits vergleichen, etwa cX (CNOT) oder cH, dann ist das Tofoli-Gate eine Erweiterung des CNOT auf zwei "kontollierende" Qubits. Entsprechend kann man auch andere 1-Qubit Gates-Gates über kontrollierende Qubits beeinflussen.
Bei 3-Qubit gibt es auch die Möglichkeit, ein controlling Qubit auf die zwei anderen Qubits wirken zu lassen. Ein Beispiel ist das cSWAP, auch Fredkin-Gate genannt. Es "swappt" die Zustände von q1 und q2 in Abhängikeit von q0.
Nicht alle Möglichkeiten für controlled Gates sind als Symbole im Circuit Composer vordefiniert. Man kann sie aber in der Regel alle aus vorhandenen Gates "konstruieren".
Die logischen Qubit Gates sind zu vergleichen mit einfachen "wenn ... dann" Konstrukten in herkömmlichen Algorithmen. Während dabei aber die Bedingung hinter "wenn" stets entweder wahr oder falsch ergibt, oder als Bits 1 oder 0, kann bei Qubits die Bedingung "anteilweise" erfüllt sein. Etwa, wenn das Control-Qubit den Zustand 1/√2(1,1) hat. Die Wirkung nach dem "dann" bezieht sich immer auf ein anderes Qubit (das controlled Qubit), während bei herkömmlichen Algorithmen die "dann"-Aktion mehrere Schritte mit mehreren Variablen haben kann - die in der "wenn"-Bedingung vorkommenden eingeschlossen.
3-Qubit-Verschränkungen
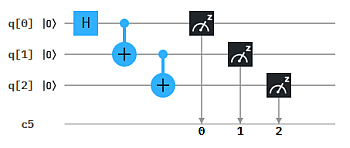Natürlich gibt Verschränkung auch in 3-Qubit (oder Mehr-Qubit) Systemen. Der Circuit sieht aus wie ien Erweiterung unseres Circuit 7 für 2 Qubits. Tatsächlich ist auch das Messergebnis ähnlich: Es liefert 000 und 111 mit jeweils etwa 50%. Das lässt sich auch anhand der Zustandsabfolge nachvollziehen (mit ein bisschen Probieren):
(1,0)⊗(1,0)⊗(1/√2,1/√2) = (1/√2, 1/√2, 0, 0, 0, 0, 0, 0)
---> CNOT-q0-q1 ---> (1/√2, 0, 0, 1/√2, 0, 0, 0, 0)
---> CNOT-q1-q2 ---> (1/√2, 0, 0, 0, 0, 0, 0, 1/√2)
Verschränkte 2- und Mehr-Qubit-Zustände spielen eine wichtige Rolle in Qubit-Algorithmen. Wir werden das in den nächsten Blogs demonstrieren.
Man kann nun untersuchen, was passiert, wenn man dem q1 und / oder dem q2 ein X-Gate voranstellt, d.h. nicht mit dem Anfangszustand (1,0) sondern mit (0,1) startet. Das Einfachste, wenn man den Zugang zum IBM Q Experience Circuit Composer hat, ist Ausprobieren. Andererseits kann man das auch erschließen. Z.B. hat ein X auf der q1-Linie den Effekt, als Messergebnis 001 und 110 zu liefern, also gegenüber 000 und 111 eine Umkehrung des (rechten) Ergebnis-Bit aus dem Zustand von q0. In jedem Fall bekommen wir eine Verschränkung der 3 Qubits.
Diese Zustandsverschränkung wird als GHZ-Verschränkung bezeichnet - wie überhaupt in der Qubit-Welt viele Objekte mit Namen von Forschern bezeichnet oder abgekürzt werden. Damit wollen wir uns hier aber nicht belasten. Ganz am Ende der Blogserie gibt es dann noch mal eine Tabelle dafür. Ein weiterer wichtiger Verschränkungszustand heißt "W-Zustand". Den werden wir im nächsten Blog kennen lernen. Und unterwegs werden wir einen ersten "richtigen" Qubit-Algorithmus konstruieren, der etwas Reales tut: "Würfeln". Klingt simpel? Ist es aber nicht.
Kleine Pause, dann geht's hier weiter. Stay tuned!
Tabellen-Ergänzung
| Begriff englisch | Begriff deutsch | Bedeutung |
| Swap Gate | Swap Gate | Vertauscht die Zustände zweier Qubits |
| 3-Qubit State | 3-Qubit-Zustand | (r,s)⊗(u,v)⊗(x,y) in Koordinatenschreibweise |
| |ijk> | |ijk> | 3-Qubit-Zustand in Ket-Schreibweise: |ijk> = |i>⊗|j>⊗|k> |
| associative | assoziativ | Reihenfolge der Ausführung der Operation ist beliebig z.B. (a+b)+c = a+(b+c). |
| commutative | kommutativ | Reihenfolge der Operanden ist beliebig, z.B. a+b=b+a. Aber nicht a-b = b-a! |
| Tofoli-Gate | Tofoli-Gatter | ccX: Switch q3, wenn q0 und q2 im Zustand (0,1) |
| Fredkin-Gate | Fredkin-Gatter | cSwap: Swappt Zustände von q2 und q3, wenn q0 in (0,1) |
| GHZ | GHZ | Ein verschränkter 3-Qubit-Zustand |
| W state | W-Zustand | Ein anderer 3-Qubit verschränkter Zustand |
Q10 Qubit-Algorithmen - Hinter die Kulissen geschaut
"Hinter die Kulissen schauen" - das heißt, die Effekte der Zwei- und Mehr-Qubit Algorithmen durch Zustandsübergänge zu erklären. Das ist, zugegeben, nicht ganz so einfach wie bei herkömmlichen Algorithmen, bei denen wir die Variablen - als Pendant zu den Qubits - einfach setzen, verrechnen und zu jeder Zeit "ansehen" können (print).
In Q9 hatten wir die Darstellung von Qubit-Zuständen für 2-Qubit Systeme eingeführt - in Form von Vierer-Koordinaten und, alternativ, in Ket-Schreibweise. Damit können wir nun einige elementare Qubit-algorithmische Komponenten nachvollziehen. In Q9 hatten wir eine Reihe von Circuit-Beispielen grafisch erstellt und vom IBM Qubit-Simulator ausführen lassen. Einige davon wollen wir anhand der Zustandsübergänge untersuchen und so erklären, wie es zu den Messergebnissen kommt. Besonders interessiert uns natürlich das Phänomen der Verschränkung und, was es mit dem Kick-back auf sich hat.
Zwei-Qubit-Zustände können durch vier Koordinaten (w, x, y, z) dargestellt werden, die |w|²+|x²|+|y|²+|z|²=1 erfüllen. Also Punkte auf einer Art 4-dimensionalem Einheitskreis.
Wenn der Zustand aus einer Kombination von zwei Qubit-Zuständen, sagen wir (u,v) und (x,y), entsteht, dann sind die vier Koordinaten durch (u,v)⊗(x,y) = (ux, uy, vx, vy) bestimmt. Die Reihenfolge ist übrigens nicht vertauschbar! Und wir hatten per Circuit-Simulation und Nachrechnen schon gesehen, dass nicht jeder 2-Qubit-Zustand sich aus zwe 1-Qubit-Zuständen zusammensetzt (Verschränkung).
Zustände und Gates
Wir hatten schon in Q7 gesehen, dass man die 1-Qubit-Gates X und H durch die Koordinaten (x,y) eines Zustands ausdrücken kann:
X(x,y) = (y,x) und H(x,y) = 1/√2(x+y,x-y)
Ry hat einen Parameter, θ, der einen Drehwinkel beschreibt. Daher ist nicht Ry ein Gate sondern Ry(θ). Angewendet auf den Zustand (x,y), den man auch mittels seines Winkels auf dem Einheitskreis als (cos(α),sin(α)) ausdrücken kann, wirkt Ry(θ) auf (x,y) als "Bewegung" auf dem Einheitskreis um θ/2. Als Formel also
Ry(θ)(x,y) = (cos(α+θ/2),sin(α+θ/2))
(Das θ/2 ist wieder nötig, weil der Ry-Paramter eine andere Bedeutung hat als der Drehwinkel auf unserem Einheitskreis.) Man kann das immer überprüfen durch Tests mit einfachen Composer-Circuits.
Aber was ist mit dem CNOT Gate, dass ja zwei Qubit-Zustände "verknüpft"? Nehmen wir wieder (u,v)⊗(x,y) = (ux, uy, vx, vy) als generelles Beispiel. Dann ist
CNOT angewendet auf (u,v)⊗(x,y) = (ux, vy, vx, uy)
d.h. die 2. und 4. Koordinate werden vertauscht. Aber wie können wir das begründen? Und welcher von beiden ist der "controlling" (steuernde) Qubit-Zustand und welcher der "controlled" (gesteuerte)? Wir überprüfen das mit dem Effekt auf die Basiszustände in Koordinatendarstellung. Wir erinnern uns dennoch, dass (1,0) dem Ket |0> entspricht und (0,1) dem Ket |1>.
(0,1)⊗(1,0) = (0, 0, 1, 0) ---> CNOT ---> (0, 0, 1, 0) = (0,1)⊗(1,0) gleich
(0,1)⊗(0,1) = (0, 0, 0, 1) ---> CNOT ---> (0, 1, 0, 0) = (1,0)⊗(0,1) ungleich
(1,0)⊗(1,0) = (1, 0, 0, 0) ---> CNOT ---> (1, 0, 0, 0) = (1,0)⊗(1,0) gleich
(1,0)⊗(0,1) = (0. 1, 0, 0) ---> CNOT ---> (0, 0, 0, 1) = (0,1)⊗(0,1) ungleich
Die Zustände der beiden Qubits bleiben nach CNOT gleich, wenn der zweite Zustand (rechts) (1,0) ist. Das entspricht dem Ket |0>. Der linke Zustand ändert sich, wenn der rechte (0,1) ist, was dem Ket |1> entspricht. Der rechts vom ⊗ stehende Zustand verändert sich in keinem Fall. Damit ist klar, dass der Zustand von q0 im Circuit 7 (Control Qubit) in der Formel rechts stehen muss, und der von q1 (Controlled Qubit) links im ⊗-Ausdruck. Merkregel: Das passt zu den Bit-Ketten, die beim Messen der Circuits geliefert werden: von q0 ganz rechts bis q4 ganz links.
Nur zur Übung hier die vierte Zeile "übersetzt" in die Ket-Schreibweise.
|0>⊗|1> = |01> = 0*|00>+1*|01>+0*|10>+0*|11>
---> CNOT
---> 0*|00>+0*|01>+0*|10>+1*|11> =|11> = |1>⊗|1>
das q1 hat seinen Zustand von |0> auf |1> geändert, da q0 den Zustand |1> hat.
Wer Lust hat, kann die anderen CNOT-Transformationen ebenfalls in Ket-Schreibweise versuchen. (Die Kommentare unten werden gelesen!)
Verschränkte Qubits
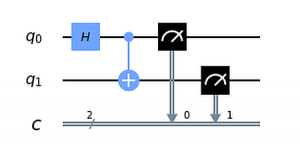Hier noch einmal der Circuit 7, der uns eine Verschränkung der Qubits q0 (obere Leitung) und q1 (untere Leitung) bescherte. Bisher konnten wir nur die Messergebnisse interpretieren. Mit den Formeln für H und CNOT können wir den verschränkten 2-Qubit Zustand bestimmen.
Die Ausgangszustände der beiden Qubits sind (1,0). Wenn H auf q0 angewendet wird, bekommen wir 1/√2(1,1) nach der Formel oben. Das CNOT müssen wir daher mit diesem Zustand als Control auf den Zustand von q1 anwenden, d.h. (1,0) steht links vom ⊗:
(1,0)⊗(1/√2,1/√2) = (1/√2, 1/√2, 0, 0) ---> CNOT ---> (1/√2, 0, 0, 1/√2) = ???
Das Ergebnis von CNOT ist 1/√2(1,0,0,1) und das ist, wie wir in Q9 gesehen haben, nicht separabel, d.h. in zwei einzelne Qubit-Zustände zerlegbar.
Im Beispiel 2 des vorigen Blogs (Q9) hatten wir die Variante mit einem X-Gate auf der q1-Linie, vor dem CNOT, diskutiert. In der vorausgegangenen Rechnung würde daher ganz links ein (0,1) stehen, statt (1,0). Was wäre dann hier der Zustand bei Messung? Und ist der separabel oder verschränkt?
Kick-back Qubit 0
Im Blog Q9 hatten wir mit Beispiel 6 einen überraschenden Effekt, der als Kick-back bezeichnet wird. Der Algorithmus im Composer-Format sah so aus:
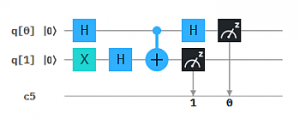Die Messungen ergeben 01 und 11 zu je etwa 50%.
Wir versuchen das mittels der Abfolge der Zustände, die wir ja theoretisch berechnen können, zu verstehen. Wir verwenden dazu die Koordinaten-Darstellung der Zustände.
Qubit q0 beginnt im Zustand (1,0) und wird per H in (x,y) = 1/√2*(1,1) überführt. Qubit q1 beginnt im Zustand (1,0) und wird von X in (0,1) überführt. Darauf wird H angewendet, das nach der Formel oben den Zustand von q1 in (u,v) = 1/√2*(1,-1) überführt. Das 2-Qubit System hat damit den zusammengesetzten Zustand
(u,v)⊗(x,y) = (ux, uy, vx, vy) = 1/2*(1, 1, -1, -1)
---> CNOT (Vertauschen der zweiten und vierten Koordinate)
---> 1/2*(1, -1, -1 ,1) = 1/√2*(1,-1)⊗1/√2*(1,-1)
Nun überführt H, auf q0 im Zustand 1/√2*(1,-1) angewendet, q0 in (0,1). Qubit q1 bleibt in 1/√2*(1,-1). Wir stellen damit fest:
- Der 2-Qubit Zustand ist nicht verschränkt. Beide Qubits sind separat messbar.
- Messung von q0 liefert immer 1, Messung von q1 liefert 0 und 1 zu 50%. Damit erwarten wir die 2-Qubit Zustände 01 und 11 zu 50%.
Das controlled Qubit hat damit eine Rückwirkung (Kick-back) auf das q0. Es kehrt den Zustand von q0 zu (0,1) um, obwohl HH(1,0) = (1,0) zu erwarten wäre. Wir werden das Kick-back später in einem komplexeren Algorithmus geschickt einsetzen. (Zur Übung lohnt es sich, diese Rechnung auch in Ket-Form durchzuführen.)
Mehr Gates, mehr Qubits
Bisher haben wir folgende Gates und ihre Formeln für die Zustandsüberführung kennen gelernt: Das X, H und Ry für 1-Qubit Zustände, sowie ein "Reset"-Gate, das im Composer schlicht als |0> gekennzeichnet wird. Damit kann man im Verlauf der Zustandsentwicklung ein Qubit auf den Ausgangszustand zurücksetzten.
Das Instrumentarium der Qubit-Algorithmik enthält noch eine Reihe von weiteren Gates, die auch in einem Circuit eingesetzt werden können. Einige davon, die wir in unseren Blogs gebrauchen können, sind hier kurz erklärt. Wer Lust hat kann deren Wirkung unmittelbar in einfachen Circuits einmal ausprobieren - dabei ist aber zu beachten, dass verschiedene Zustände durchaus das gleiche Messergebnis liefern können.
- Y-Gate: Hat für unsere Zwecke die gleiche Wirkung wie X.
- Z-Gate: Überführt 1/√2*(1,1) in einem Schritt in 1/√2*(1,-1), und umgekehrt. Für diese beiden Zustände gibt es übrigens ein besonderes Ket-Symbol: |+> und |->. Es ist offensichtlich, welches Ket welchen Zustand kennzeichnet. Das Z-Gate überführt also |+> in |->. Klingt etwas exotisch, ist aber oft eine ganz praktische "Abkürzung". Beide Zustände liefern natürlich das gleiche Messergebnis, daher kann man die Wirkung von Z nicht unmittelbar an der Messung ablesen.
- ID-Gate: Typisch Mathematik bzw. Informatik, es gibt immer auch eine Operation, die nichts verändert.
- Zwei-Qubit Gates:
- Swap-Gate, symbolisiert durch die zwei X, die übereinander stehen und mit einer senkrechten Linie verbunden sind: Vertauscht die Zustände der beiden betroffenen Qubits
- cH, controlled H-Gate: Analog zum CNOT führt es H für das controlled Qubit aus, wenn das controlling Qubit im Zustand |1> ist.
- Controlled Z-Gate, symbolisiert durch die zwei mit einem senkrechten Linie verbundene Punkte: Analog zum CNOT führt es Z für das controlled Qubit aus, wenn das controlling Qubit im Zustand |1> ist.
- Das Tofoli-Gate ist ein 3-Qubit Gate. Um das zu verstehen müssen wir zunächst unsere Zustandsbeschreibungen auf 3-Qubit Zustände erweitern.
Das machen wir gleich im Anschluß, ohne große Pause. Wir holen uns nur schnell einen Kaffe oder ein stilles Wasser. Dann gehts hier weiter.
Hier noch ein paar neue Begriffe aus diesem Anschnitt in Fortführung der tabellarischen Übersicht.
| Begriff englisch | Begriff deutsch | Bedeutung |
| CNOT-Gate | CNOT-Gatter | Controlled NOT - CNOT verknüpft zwei Qubits. In Abhängigkeit vom Zustand des einen Qubits ändert sich der des anderen. |
| Control | Control | Qubit, dessen Zustand beim CNOT Gate den des anderen "steuert" |
| Controlled | Controlled | Qubit, dessen Zustand beim CNOT Gate durch den des anderen "gesteuert" wird. |
| Y, Z, ID | Y, Z, ID | Weitere 1-Qubit Gates |
| 2-Qubit Gates | 2-Qubit Gates | Gates, die sich über zwei Qubits erstrecken |
| Swap-Gate | Swap-Gatter | 2-Qubit Gatter, vertauscht die Zustände zweier Qubits |
| cH-Gate | cH-Gatter | Controlled H-Gate, analog CNOT für H |
| cZ-Gate | cZ-Gatter | Controlled Z-Gate, analog CNOT für Z |
| Tofoli-Gate | Tofoli-Gatter | Ein controlled 3-Qubit Gate. Eine Art Erweiterung des CNOT auf 2 steuernde Qubits. |
| |+>, |-> | |+>, |-> | Ket-Bezeichnung für 1/√2(1,1) bzw. 1/√2(1,-1) |
Q9 Verschränkung und andere 2-Qubit Phänomene
Der Einsatz des CNOT Gates in Q8, Beispiel 7 (Circuit 7), führte zu einem überraschenden Ergebnis im Vergleich zu den vorausgehenden 2-Qubit Circuits. Es gibt von den sonst möglichen vier 2-Bit Messergebnissen nur die Ergebnisse 00 und 11 aus. Die beiden Qubits sind scheinbar "gleichgeschaltet". Man bezeichnet dieses Phänomen in der Qubit-Welt auch als Verschränkung (entanglement). Warum, das wird weiter unten noch genauer erklärt.
Es drängen sich eine ganze Reihe von Experimenten mit Varianten von Circuit 7 auf, von denen wir uns einige ansehen wollen. Wir werden dabei nicht immer die Composer-Grafik dazu einfügen. Wer Lust hat, kann sich das Bild dazu aufmalen. Noch besser und spannender wäre es, die 2-Qubit Circuits nicht nur zu diskutieren, sondern selbst mit dem IBM Q Experience Simulator auszuprobieren. Der Zugang ist, wie gesagt einfach und in einem eigenen Blog kurz beschrieben, und das Erstellen und Testen im Composer ist ebenfalls "Drag&Drop"-leicht.
2-Qubit Circuits
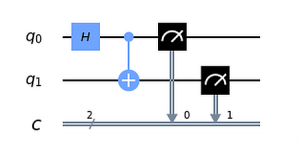
Hier zunächst noch einmal die Ausgangsgrafik des "Circuit 7", der 00 und 11 mit der Häufigkeit 0.5 liefert.
1. Was würde passieren, wenn wir vor das H-Gate noch ein X einfügen würden? Einfache Überlegung: Der Startzustand |0> von q0 würde zunächst in |1> verändert. H angewendet auf |1> ergibt 1/√2 (|0>- |1>) (s. Q8, Beispiel 6). Der Unterschied zu Circuit 7 ist also das Minus-Zeichen. Nach CNOT mit q1 macht das aber keinen Unterschied im Messergebnis, denn die Häufigkeiten von 0 und 1 entsprechen dem Quadrat der Koeffizienten. Und (-1/√2)² ist das Gleiche wie (1/√2)². Damit erwarten wir das gleiche Ergebnis wie bei Circuit 7. Das Simulationsergebnis bestätigt dies.
2. Was wäre, wenn X auf q1 vor CNOT angewendet würde? Dann ist q1 vor CNOT im Zustand |1>. Für q0 im Zustand |1> ändert sich dann q1 zu |0>, sonst bleibt es |1>. Wie demnach zu erwarten, liefert die Messung nun 01 und 10 zu je rund 50%. Wir haben hier also einen Circuit der "Ungleichschaltung". Wenn wir bei einem Qubit z.B. eine 0 messen, wissen wir, dass das andere 1 ergeben muß. Und umgekehrt. Wir haben hier also auch eine Form der Verschränkung.
3. Was ist ausschlaggebend für das Verschränkungsphänomen? Ist es das H-Gate? Was ein X-Gate zusätzlich bewirkt, bei q0 oder q1, haben wir schon gesehen. Versuchen wir es mal mit anderen Gates und testen das mit dem Simulator. Bleiben wir zunächst bei Qubit 0 und ersetzen das H durch X bzw. durch unsere Rotation Ry.
Ersetzen wir H durch X, können wir das Ergebnis einfach vorhersagen: X verkehrt den Ausgangszustand, also ist q0 bei CNOT im Zustand |1>, damit wird q1 umgekehrt, also |1>. Wir bekommen determiniert das Ergebnis 11 bei 100% der Messungen.
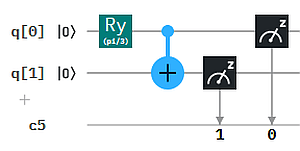Ersetzen wir H durch Ry mit dem Gate-Parameter π/3, dann wird der Startzustand von q0 im x-y-Koordinatensystem um 30º gedreht.
Als Simulatorergebnis (1024 shots) bekommen wir: 74% 0000, 26% 0011.
D.h. wir finden wieder eine "Gleichschaltung" der Zustände wie in Circuit 7, allerdings mit einer anderen Häufigkeitsverteilung. Die entspricht der Häufigkeitsverteilung bei einer 1-Qubit Anwendung von Ry(π/3) in Q8, Beispiel 3b. Offenbar ist das Vorliegen einer Superposition für q0 ausschlaggebend für Verschränkung. Wir werden später sehen, ob die Vermutung stimmt.
4. Nun zu q1. Was passiert, wenn wir q1 in eine Superposition versetzen, z.B. mittels H.
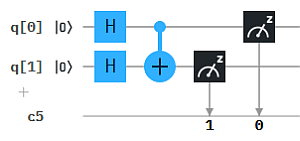Als Simulationsergebnis bekommen wir hier eine Häufigkeitsverteilung über alle 4 Möglichkeiten. Z.B.:
| Bit-Ergebnis | H | Ry(π/3) |
| 0000 | 26% | 36% |
| 0001 | 25% | 11% |
| 0010 | 23% | 13% |
| 0011 | 26% | 40% |
Setzen wir statt H die Rotation Ry(π/3) ein, ergibt sich das enstprechende Bild (rechte Spalte) zu rund 3/8, 1/8, 1/8, 3/8.
Die beiden Beispiele zeigen offenbar keine Verschränkung, sondern eine Verteilung über alle 4 möglichen Messergebnisse. Wenn wir aufgrund der Experimente mit den Varianten eine Vermutung anstellen wollten, dann die, dass CNOT eine Verschränkung (ob gleich oder ungleich geschaltet) nur dann liefert, wenn eines der Qubits in einem Basiszustand ist. Wir werden diese Vermutung weiter unten "rechnerisch" untersuchen.
5. Bisher haben wir zusätzliche Gates immer vor das CNOT geschaltet. Was ist, wenn wir das im verschränkten Zustand tun? Die einfachste Variante ist, ein X-Gate nach dem CNOT auf die q1-Leitung zu setzen. Also so:
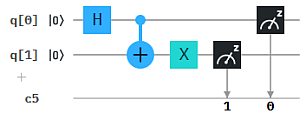Was würde man erwarten? Vor dem X-Gate ist der Zustand des 2-Qubit-Systems verschränkt bzgl. 00 und 11. Danach findet man als Messergebnis die "Umkehrung", 01 und 10. Das gleiche finden wir, wenn wir das X-Gate auf q0 setzen. Schalten wir dagegen für beide Qubits ein X-Gate nach, bleibt das Ergebnis 00 und 11 zu je 50%. Macht man die gleichen Tests mit dem H-Gate anstelle des X-Gate, bekommt man - und das ist nicht mehr ganz so überraschend - bei einem H-Gate jeweils eine Verteilung über alle 4 Möglichkeiten, bei H auf beiden Wires wiederum das Ergebnis 00 und 11 zu je 50%.
Es sei betont, dass wir immer nur die Messergebnisse sehen. Was mit den Zuständen passiert, können wir erst untersuchen, wenn wir ein formale Beschreibung für Systeme aus zwei oder mehr Qubits haben.
6. Ein algorithmisches Beispiel kann uns aber doch noch überraschen. Es ist gleichzeitig ein ziemlich wichtiger Baustein für Qubit-Algorithmen. Das Schaltbild dazu ist
Das Ergebnis ist - 01 und 11 zu je 50%! Das scheint zu keinem der bisherigen Ergebnisse zu passen. Ohne das nachgeschaltete H-Gate für q0 bekommen wir, wie zu erwarten, das Ergebnis von Beispiel 4, also alle vier Ergebnismöglichkeiten zu 25%. Abgesehen davon, wissen wir, dass H, zweimal hinternander auf |0> angewandt, wieder |0> ergbit.
Es würde uns jetzt nicht wundern, wenn es auch eine Circuit-Variante gibt, die 00 und 10 liefert. Richtig, ohne das X-Gate, also die initiale Umkehrung des Startzustands von q1! Wenn wir beides zusammen betrachten, sieht es so aus, als ob das Ergebnis von Qubit q0, das rechte der zwei Bits, durch q1 umgeschaltet. Durch das CNOT sollte aber doch eigentlich q0 das q1 beeinflusst. Trotzdem, dieser Effekt ist korrekt und hat den schönen Namen (phase) kickback - das von q0 gesteuerte q1 "schlägt zurück". (Wir werden davon in Q15 interessanten Gebrauch machen.)
Es gibt noch zwei weitere Ergebnisse ähnlicher Art, nämlich 00 und 01 zu 50% und 10 und 11 mit je 50%. Es ist interessant zu versuchen, 2-Qubit Circuits zu konstruieren, die diese Ergebnisse liefern. Wer Lust hat, möge das mit dem IBM Composer ausprobieren.
2-Qubit Zustände
Um das zu verstehen, müssen wir uns mit den "Formeln" für Zwei- und Mehr-Qubit-Systeme befassen. Zunächst mal für 2-Qubit-Systeme, auch 2-Qubit-Register genannt, in Anlehnung an das Bit-Register, der zentralen Komponente eines herkömmlichen (Bit-)Prozessors.
Wir erinnern uns, dass wir Qubit-Zustände als Punkte auf dem Einheitskreis im x-y-Koordinatensystems beschreiben können. Also z.B. (x,y) = (1/√2, -1/√2). Eine etwas andere Schreibweise, die häufig verwendet wird aber das Gleiche bedeutet, ist die, einen Qubit-Zustand als Kombination der Basis-Zustände (1,0) und (0,1) zu schreiben, für die außerdem die (aus der Quantenphysik stammenden) Symbole |0> und |1> verwendet werden. Das mag verwirren; es ist aber manchmal leichter einen Qubit-Zustands-Sachverhalt mal in der einen oder der anderen Form zu beschreiben. Man mache sich klar, dass (x,y) und x*(1,0)+y*(0,1) und x*|0>+y*|1> das Gleiche ausdrücken. Aus historischen Gründen nennt man diese Schreibweise die Ket-Schreibweise - statt z.B. "Rechts-Spitzklammer"-Schreibweise - und nennt ein Symbol |a> für einen Qubit-Zustand ein ket, bzw. ket-a.
Was ist nun der Zustand eines 2-Qubit-Systems? Eigentlich nur die Kombination von zwei Qubit-Zuständen nach der Methode "jeder mit jedem". (Wem das zu unmathematisch klingt, kann sagen, es ist das Tensorprodukt der beiden.) Haben wir also ein Qubit q0 im Zustand (u,v) und q1 im Zustand (x,y), so ist der Zustand des 2-Qubit-Systems (ux, uy, vx, vy). Er besteht also aus 4 Koordinaten, die sich aus der Multiplikation der Koordinaten der beiden Qubit-Zustände ergibt. Hier sind einige übliche Schreibweisen, an die man sich wohl gewöhnen muß - es steckt aber immer das Gleiche dahinter:
(u,v)⊗(x,y) = (ux, uy, vx, vy)
oder, wenn wir in der Ket-Schreibweise den Zustand von q0 mit |a> und den von q1 mit |b> symbolisieren
|a>⊗|b> = (ux, uy, vx, vy), wenn wir |a>=u*|0>+v*|1> und |b>=x*|0>+y*|1> für die Zustände von q0 und q1 schreiben.
Wenn man den 2-Qubit-Zustand so beschreibt, stellt man fest, dass erfreulicherweise die 4 Koodinaten wieder auf einem 4-dimensionalen "Einheitkreis" liegen. Das ist schwer vorzustellen, aber einfach als Formel auszudrücken:
|ux|²+|uy|²+|vx|²+|vy|² = 1
Da die Einzel-Zustände auf dem "normalen" Einheitskreis liegen, also |u|²+|v|²=1 und |x|²+|y|²=1, ergibt sich das einfach durch Ausrechnen von (|u|²+|v|²)* (|x|²+|y|²).
Wir konstruieren uns einige Beispiele und zeigen sie in der Tabelle in Koordinatenform. In der rechten Spalte ist das jeweilige 2-Zustands-Messergebnis dargestellt, also das, was wir z.B. bei den Messungen entsprechender 2-Qubit Circuits erwarten können.
| Koordinaten | Koordinaten | Messung | |
| q0 | q1 | 2-Qubit-Zustand | 2-Bit Ergebnis : Häufigkeit |
| (1,0) | (1,0) | (1,0,0,0) | 00: 1.0 |
| (1,0) | (0,1) | (0,1,0,0) | 01: 1.0 |
| (0,1) | 1/√2*(1,1) | 1/√2*(0,0,1,1) | 10: 0.5 11: 0.5 |
| (u,v) | (x,y) | (ux,uy,vx,vy) | 00: |ux|² 01: |uy|² 10: |vx|² 11: |vy|² |
Zum Vergleich - und zur Gewöhnung - schreiben wir die Tabelle noch einmal in Ket-Schreibweise. (Die Messergebnisse sind die gleichen.)
| q0 - Ket | q1 - Ket | 2-Qubit-Zustand - Ket |
| |0> | |0> | 1*|00> |
| |0> | |1> | 1*|01> |
| |1> | 1/√2*(|0>+|1>) | 1/√2*(|10>+|11>) |
| u|0>+v|1> | x|0>+y|1> | ux|00>+ uy|01>+ vx|10> + vy|11> |
Etwas fällt vielleicht noch auf: die Kets mit zwei Ziffern, etwa |01>. Das ist einfach wieder eine abkürzende Schreibweise für |0>⊗|1>, also die Kombination von zwei Qubit-Zuständen (in Ket-Schreibweise) zu einem 2-Zustands-Ket.
Die Ket-Schreibweise erleichtert bei Zwei- und Mehr-Qubit-Zuständen die Sicht auf die Messergebnisse. Der Operator M, auf einen allgemeinen 2-Qubit-Zustand (w, x, y, z) angewendet liefert die Wahrscheinlichkeiten |w|², |x|², |y|², |z|². Aber was ist was? Man kann sich merken, dass |w|² für Bitfolge 00 der Messung, |x|² für 01 usw. gilt. Schreibt man den Zustand in Ket-Form, dann sieht man es sofort. Denn (w,x,y,z) = w|00> + x|01> + y|10> + z|11>. Damit ist, bei 2-Qubit-Zuständen,
M(w,x,y,z) = ( |w|², |x|², |y|², |z|²)
eine "theoretische Formel" für den Messvorgang. Gemessen wird der Zustand, das Ergebnis (rechts) sind Wahrscheinlichkeiten für die 2-Bit-Folgen. Man hat hiermit also eine Verknüpfung zwischen Qubits und klassichen Bits.
Um Verwirrung zu vermeiden, werden wir allerdings im Weiteren vorzugsweise die Koordinaten-Schreibweise verwenden.
Verschränkte 2-Qubit-Zustände
Im Prinzip kann man alle Punkte im 4-dim Koordinatensystem, die als Summe ihrer Quadrate 1 ergeben, als 2-Qubit-Zustände betrachten. Bei Messungen ergäben sich aus solchen Zuständen die Quadrate der Koordinaten als Häufigkeitsverteilung über die vier möglichen (Bit-) Messergebnisse 00, 01, 10, 11. D.h. beliebige 4 Zahlen (w, x, y, z) mit |w|²+|x²|+|y|²+|z|²=1 ergeben einen zulässigen 2-Qubit-Zustand.
Allerdings, nicht jeder Zustand in dieser Form lässt sich - wie oben - aus den Zuständen von zwei Qubits herstellen! Das ist verblüffend, aber lässt sich leicht überprüfen.
Circuit 7, oben, lieferte als Messung 00 und 11 mit Häufigkeit 0.5, und 01 bzw 10 mit Häufigkeit 0. Wenn der (unbekannte) 2-Quibt-Zustand, der zu dieser Messung führt, eine Kombination (u,v)⊗(x,y) = (ux, uy, vx, vy) von zwei Qubits wäre, müssten |ux|² = |vy|² = 0,5 sein und gleichzeitig |uy|² = |vx|² = 0. D.h. einerseits müssen u,x,v und y ungleich Null sein, andererseits müssen u oder y, sowie v oder x Null sein. Das ist offensichtlich ein Widerspruch.
Der Zustand, der in Circuit 7 gemessen wird, ist damit ein zulässiger und herstellbarer 2-Qubit-Zustand. Er kann aber nicht aus zwei Qubits zusammengesetzt werden, oder, anders ausgedrückt, er ist nicht separierbar. Das System aus zwei Qubits, das in einen nicht-separierbaren 2-Qubit-Zustand überführt wird, ist verschränkt. Das ist es, was dahinter steckt! Man mag nun selber überprüfen, welche der Circuits oben ebenfalls verschränkte Zustände liefern. (Wer Lust hat - der Kommentar-Bereich steht offen.)
Eine Konsequenz der Verschränkung ist, dass man nicht von den Zuständen der beiden Qubits sprechen kann. Im eigentlichen Sinne haben sie keinen Zustand. Allein das Gesamtsystem hat einen Zustand. Insofern kann man auch nur das Gesamtsystem messen, nicht die "involvierten" Qubits.
Die Wirkung von Gates
Mit Hilfe der Zustandsbeschreibungen können wir nun auch die Wirkung von Gates "berechenbar" machen. D.h., obwohl wir sie nicht per Messung verfolgen können, lässt sich die Abfolge der Zustände rechnerisch darstellen.
Das machen wir im nächsten Blog-Beitrag; denn jetzt haben wir uns spätestens eine Pause verdient, bei der wir entspannt noch mal über alles nachdenken können.
Hier geht's dann anschließend weiter.
Stay tuned!
Hier noch ein paar neue Begriffe aus diesem Anschnitt in Fortführung der tabellarischen Übersicht.
| Begriff englisch | Begriff deutsch | Bedeutung |
| Entanglement | Verschränkung | Nicht separierbarer Gesamtzustand eines 2-Qubit Systems |
| Separable | Separierbar | 2-Qubit-Zustand, der sich aus zwei Qubit-Zuständen zusammensetzem lässt. |
| Register | Register | System von zwei oder mehr Qubits auf dem algorithmische Operationen ausgeführt werden |
| Ket | Ket | Zweite Silbe von Bra-cket. Schreibweise für Qubit-Zustände |
| Symbol ⊗ | Symbol ⊗ | Symbolisiert die Kombination von zwei Qubit-Zuständen zu einem Gesamtzustand. |
| |00>, |01> etc | |00>, |01> etc | Kurzschreibweise für |0>⊗|0>, |0>⊗|1>usw. |
| (Phase) Kickback | (Phase) Kickback | Spezielle Rückwirkung zwischen CNOT verbundenen Qubits |
Q8 Fingerübungen - Einfache Qubit Algorithmen ausprobiert
Wir wissen nun, was ein Qubit ist. Genauer, wie man ein Qubit modellieren kann - aber wir wollen uns ein wenig sprachliche Vereinfachung zugestehen, solange wir uns darüber im Klaren sind. Fassen wir noch einmal zusammen:
Ein Qubit ist ein Konstrukt, das einen Zustand hat, der durch Operatoren beeinflusst wird, und der über ein Messverfahren einen binären Wert liefert (Bit). Der Zustand ist aus einer kontinuierlichen (unendlichen) Menge. Wiederholte Messungen bei gleichem Zustand liefern eine Häufigkeitsverteilung über die binären Werte, die man als Wahrscheinlichkeitsverteilung dem Zustand zuordnen kann.
Wir legen fest, dass die Operatoren den Zustand determiniert beeinflussen, mathematisch also eine Abbildung darstellen. D.h. gleicher Operator angewendet auf gleichen Zustand liefert gleiches Ergebnis (neuer Zustand). Für das Messverfahren gilt das natürlich nicht. Wohl aber für die Zuordnung der Wahrscheinlichkeitsverteilung zu einem Zustand.
In diesem Sinne ist ein klassisches Bit auch ein Sonderfall eines Qubits. Wieso?
Für die konkrete Beschreibung von Qubits verwenden wir (einfache) mathematische Ausdrücke: Die Zustände beschreiben wir durch die Koordinaten (x,y) eines Punktes auf dem Einheitskreis in der x-y-Ebene. Die binären Messwerte bezeichnen wir mit 0 und 1. Für die Punkte, die einen Zustand repräsentieren, verwenden wir gelegentlich "Namen" anstelle der Koordinaten; das macht manchmal das Lesen einfacher. Insbesondere sind folgende Bezeichnungen in der Qubit-Welt üblich: |0> für (1,0), |1> für (0,1) - also für die Punkte des Einheitskreises, die auf den positiven Koordinatenachsen liegen. (Diese Zustände hatten wir beim ZBIT-Modell mit [00] und [11] bezeichnet. Die etwas ungewöhnliche | >-Schreibweise erklären wir später. ) Damit kann man einen Zustand (x,y) auch als Kombination von |0> und |1> schreiben: x|0> + y|1>.
Ein typischer Sprachgebrauch in der Qubit-Welt ist z.B. "das Qubit |1>" an Stelle von "das Qubit im Zustand |1>". Kein Problem, wenn klar ist, was gemeint ist. "Namen" für die Qubits sind wie herkömmliche Variablen-Namen zu verstehen und werden in den Composer-Grafiken links vor die zugehörige Linie gestellt. Sie sind der Einfachheit halber durchnummeriert. Entweder als q0, q1, usw. oder im Stile von Python-Listen als q[0], q[1] usw., also mit eckigen Klammern.
Ein weiterer häufig anzutreffender Begriff für die x-y-Kombination der beiden Basiszustände ist "Superposition", übersetzt als "Überlagerung", von |0> und |1>. Ein leicht mysteriös klingender Begriff für die Kombination der beiden Zustände. Der stammt aus der Physik und wird in der Mathematik übrigens Linearkombination genannt.
Wie wir in Q7 gesehen haben, ist für x|0> + y|1> dann |y|² die Wahrscheinlichkeit p(1) für den binären Wert 1 bzw. |x|²=1-|y|² die für 0 bei der Messung des Qubits in diesem Zustand.
Man kann damit den Messvorgang, genauer, den wiederholten Messvorgang, auch als einen Operator darstellen, der Zustände (x,y) in Häufigkeiten von Bits überführt:
M(x,y) = M(x|0> + y|1>) = ( |x|², |y|²).
Bei Mehr-Qubit-Zuständen wird das, wie wir sehen werden, eine hilfreiche Darstellung. Wir bezeichnen M nicht als Gate, weil wir Gates für Übergänge von Zustand zu Zustand reservieren wollen, ( |x|², |y|²) aber kein Qubit-Zustand ist, sondern Wahrscheinlichkeiten für Bit-Ergebnisse.
Woher wissen wir, in welchem Zustand sich ein Qubit befindet? Man wählt |0> als Ausgangszustand, herstellbar durch die Operation R. Wenn wir anschließend weitere Operatoren anwenden, liefert jeder einen determinierten Folgezustand. Wenn wir die Wirkung der Operatoren berechnen können, wie in Q7 für X, H usw., können wir die Zustände nachverfolgen, wissen also bei der Messung, welcher Zustand vorliegt - auch wenn die Messung selbst nur ein Bit (0 oder 1) liefert. Dies ist ein wichtiges Prinzip, um Algorithmen für Qubits formulieren zu können.
1-Qubit Beispiele
Das wollen wir im Folgenden für einige erste kleine Beispiele mit einem bzw. zwei Qubit(s) tun und diese gleich auch auf einem Qubit-Computer realisieren.
Für einen Qubit Computer (physikalisch oder als Simulator) müssen wir fordern, dass wir die physikalischen Entsprechungen der Qubit-Operatoren so konstruieren können, dass sie - in wiederholten Messungen - Häufigkeiten eines binären Ergebnisses liefern, die der Wahrscheinlichkeit von 0 und 1 in dem Operator-generierten Zustand entprechen. Klingt kompliziert, ist es auch. Aber wir machen nichts falsch, wenn wir darauf vertrauen, dass die Quantencomputer-Konstrukteure dafür gesorgt haben.
In Q7 u.a. hatten wir schon einige 1-Qubit Algorithmen in der Form R --- X --- H --- M oder ähnlich formuliert. Diese Schreibweise kommt der grafischen Darstellung im "Composer" (Komponisten) der IBM Q Experience Umgebung schon sehr nahe. Wir probieren es einfach und lassen die "Partitur" vom Simulator ausführen. (Wie man Zugang zur IBM Quantencomputing-Umgebung bekommt, wird in diesem Blog beschrieben. Besser noch, man findet es selbst heraus. Hier ist der Link zum IBM Q Login.) Es ist wirklich zu empfehlen, diese Erfahrung "in echt" zu machen (s. Q2). Statt des Simulators kann man zur Ausführung auch einen der verfügbaren echten Quantencomputer auswählen!
1. R--- X --- H --- M
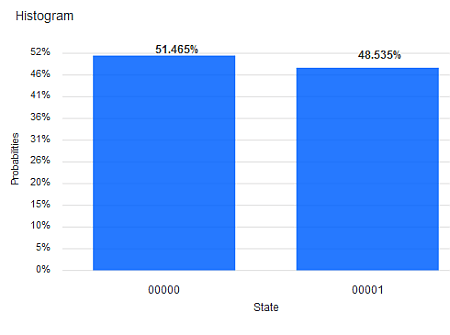
Das Ergebnis zeigt die Häufigkeiten von 0 und 1 (interpretiert als klassische Bits) bei einer Serie von 1024 Durchläufen. Die Legende der State-Achse ist für die gleichzeitige Messung von 5 Qubits ausgelegt, daher die 5-stelligen Bit-Ketten. Das Bit rechts kommt aus der Messung des Qubit Nr. 0, dem obersten im Composer, wenn wir mehrere Qubits haben. Dass die Achse mit "state" (Zustand) bezeichnet wird, ist etwas verwirrend. Gemeint ist bestenfalls der "Ausgabezustand".
Nicht ganz zufällig gibt es die hier schon verwendeten Operatoren X und H auch beim Qubit-Composer. Im Qubit-Sprachgebrauch werden die Operatoren Gates genannt, zu deutsch Gatter. Die Gates werden auf Wires (Leitungen) positioniert. Und die "Partitur" wird in der Qubit-Welt Circuit (Schaltung) genannt. Am Anfang eines Qubit-Wire ist das Qubit auf den Ausgangszustand |0> gesetzt. Das Symbol (Gate) dafür im Composer ist nicht R sondern einfach |0>. Die beiden Gates auf dem Wire von Qubit q[0] heißen X-Gate oder NOT-Gate, weil es den Qubit-Zustand umkehrt, und Hadamard-Gate (H-Gate), benannt nach dem französichen Mathematiker J. Hadamard. Die Wirkung hatten wir in Q7 bereits formelmäßig definiert.
Als ein anderes Beispiel nehmen wir aus Q7 "Vorhersagen und Erklärungen" die Nummer 8.
2. R ---- G60 ---- H ---- H ---- M
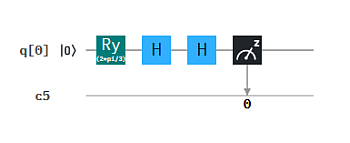
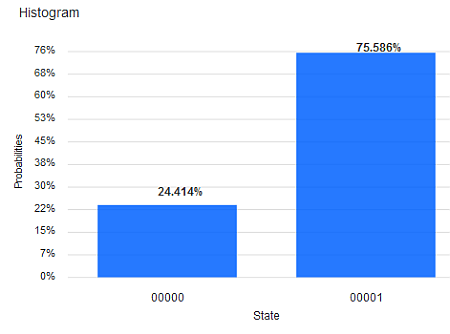
Es fällt auf, dass wir bei der QBIT-Box das Dreh-Feld mit G bezeichnet haben, im Composer aber ein neues Gate Ry(2*pi/3) verwendet haben. Mit G hatten wir in Q7 den Dreh-Operator vereinfacht. So wie wir G definiert hatten, entspricht dem das Rotations-Gate Ry mit dem Paramterwert θ=2*pi/3. Man sieht in der Tabelle am Ende von Q7, dass dieses θ dem Winkel w=60º entspricht. (Die Gates in den Composer- bzw. Programmier-Umgebungen orientieren sich an einer anderen Zustandsbeschreibung, die dazu führt, dass der Winkel, den wir für Drehungen auf dem x-y-Einheitskreis definieren, in der Composer-Beschreibung verdopplet werden muss.)
3. R --- G30 --- X --- M vergleichen wir mit R --- G30 --- M, um die Wirkung von X zu verifizieren. Hier müssen wir, wie eben erklärt, für G30 das Gate Ry mit pi/3 parametrisieren. Wir verzichten dabei auf die Histogramme und notieren stattdessen nur die Häufikeiten der Messergebnisse.
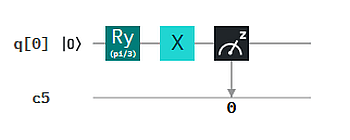
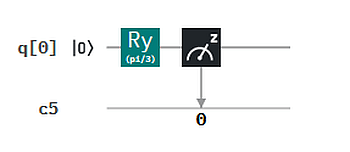
Man sieht also sehr schön den Effekt eines X-Gates aus der wiederholten Messung: Es vertauscht die Zustandskoordinaten. Für die Basis-Zustände ergibt sich daraus: X: |0> -> |1>, d.h. (1,0) -> (0,1), und umgekehrt. Wir merken an, dass wir hier wieder von den Messergebnissen (Bits) auf den Zustand (Qubit) nach Anwendung der Gates schließen. Die Messergebnisse sind nicht der Zustand!
4. R --- Gw --- M. Das Diagramm der QBIT-Box Experimente in Q7 (blaue Punkte) ist natürlich auf diese Weise (3b) entstanden! Das w durchlief alle Werte von 0º bis 360º (das entspricht θ=2*pi) in 15º-Schritten. Für jedes w wurde ein Cirquit der Form 3b) erzeugt, der jeweils 50 Mal durchlaufen wurde. Die Häufigkeiten von 1 (das entspricht dem L) wurden in die Grafik eingetragen. Das Ganze wurde natürlich in Form eines kleinen (Python-)Programms durchgeführt. Im Kern einer Schleife über die verschiedenen Winkel steht dabei das Python-Pendant zum Composer Circuit:
## Circuit definieren q_box = QuantumCircuit(q, c) rot = k*2*pi/m q_box.ry(rot,q) q_box.measure(q[0], c)
Etwas ausführlicher wird das Programm in einem Kommentar zu diesem Blog gezeigt.
2-Qubit Beispiele
Bevor wir uns theoretisch mit Zwei- und Mehr-Qubit Kombinationen befassen, probieren wir einfach einmal ein paar Beispiele mit dem Composer praktisch aus. Wir müßten dazu natürlich auch unsere einfache Schreibweise für Qubit-Algorithmen erweitern, etwa zwei Zeilen untereinander. Das stimmt aber ziemlich genau mit den Composer Grafiken überein, die wir bereits in Abschnitt Q2 erkundet hatten. Daher formulieren wir die kleinen Algorithmen gleich als Circuit.
5. Probieren wir es mal mit
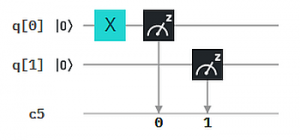und versuchen zu verstehen, was wohl als kombiniertes Messergebnis herauskommen wird. Der Ausgangszustand von Qubit 0 (q0-Wire) wird mit X zu |1> und dann gemessen. Qubit 1 (q1-Wire) wird sofort gemessen, bleibt also im Zustand |0>. Grundsätzlich gibt es 4 mögliche Messergebnisse, nämlich die vier 2-Bit Kombinationen 00, 01, 10, 11. Das Ergebnis hier ist natürlich 100% 01.
Zur Erinnerung (an Abschnitt Q2): Auf der c-Linie kommen die Messergebnisse an - in Form von klassischen Bits (c für classical). Die 5 deutet an, dass die c-Linie die Ergebnisse von bis zu 5 Qubits aufnimmt (s. Histogram nächstes Beispiel), auch wenn wir hier nur 2 Qubits verwenden.
6. Etwas schwieriger:
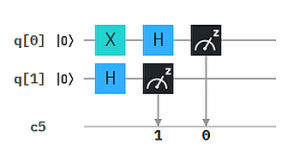Hier wird q0 zunächst geswitcht und dann mit dem Hadamard-Gate transformiert. D.h. |0> wird zu 1/√2 (|0> - y|1>), oder in Koordinaten wie in Q7 zu 1/√2(1,1). Die Wahrscheinlichkeiten für 0 und 1 als Messergebnis sind damit 1/2. Für q1 wird nach H der Zustand 1/√2 (|0>+y|1>) gemessen, was die gleichen Wahrscheinlichkeiten für Qubit 1 ergibt. Was ist also das Gesamtergebnis (1024 "shots")?
Hier zählen nur die zwei rechten Bits, so dass also die experimentellen Häufigkeiten um den zu erwartenden Wert 0.25 schwanken. (Die Konvention ist, das Bit-Ergebnis von q0 immer ganz rechts zu schreiben.)
7. Das Hello Qubit World Beispiel aus Q2 sah als "Partitur" so aus:
Hier finden wir nach dem H ein neues Gate, das offenbar zwei Qubits miteinander in Beziehung bringt. Das ist das Controlled-Not-Gate, auch als CNOT oder CX bezeichnet. Es beeinflußt q1 - da, wo das + im Kreis steht - in Abhängigkeit vom Zustand des Qubit q0. Genauer: wenn q0 im Zustand |1> ist, kehrt sich q1 um - hier also von |0> nach |1>. Ansonsten bleibt der Zustand von q1 unverändert, also hier |0>.
Schauen wir uns das Ergebnis an (1024 shots).
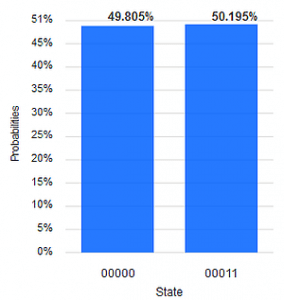Das Histogramm zeigt nur positive Werte für die 2-Bit Messergebnisse 00 und 11, zu jeweils ziemlich genau 50%. Die beiden anderen, 01 und 10, kommen bei Messungen nicht vor. Das hat verschiedene Konsequenzen, auf die wir später noch eingehen werden. Hier stellen wir erst einmal fest, dass das CNOT-Gate offenbar die beiden Qubits "gleichschaltet". Aber Achtung - nur bezüglich der Messergebnisse! Beide sind nach diesem Circuit entweder 0 oder 1, und was, das bestimmt q0. Um über die Zustände zu sprechen, müssen wir wieder unser Modell bemühen.
Damit können wir das Ergebnis noch besser verstehen: durch das Hadamard-Gate geht der q0-Zustand in die Kombination von |0> und |1> über, jeweils mit Anteil 1/√2. Daher ergibt sich der neue Zustand von q1 nach der CNOT-Regel als Kombination von |0> (unverändert) und |1> (verändert) mit den entsprechenden Anteilen von 1/√2. Und q1 kann nur 0 ergeben, wenn sein Zustand sich nicht geändert hat, also wenn q0 das Ergebnis 0 liefert. Andernfalls hätte sich q1 umgekehrt und würde 1 liefern. Das erklärt - in Worten - warum 01 und 10 nicht als Messergebnis auftreten können. Im nächsten Blog werden wir das "nachrechnen".
Die "Gleichschaltung" der beiden Qubits durch diesen Circuit bedeutet u.a., dass wir wissen können, welchen Messwert das andere Qubit hat, wenn wir nur das eine gemessen haben. Wir können aus einer Messung das Ergebnis beider Messungen erschließen! Das wirkt zunächst einmal ungewöhnlich und führt zu teilweise "geheimnisvollen" Deutungen. Doch davon später.
Ein kleiner Ausflug: Die Wires sind so etwas wie die "Lebenslinien" der beiden Qubit-Variablen q0 und q1. Sie beginnen beide in einem Anfangszustand und "enden" durch Messung. Mit etwas Phantasie kann man auch klassische Algorithmen als Composer Diagramm darstellen.
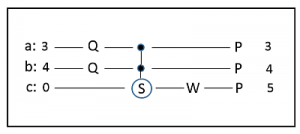
Zum Beispiel kann man die Berechnung der Hypothenusenlänge nach dem Satz des Pythagoras a²+b²=c² so in Composer-Form darstellen. Dabei sind a,b,c die Variablen, 3 ,4, 0 die Anfangszustände, Q ist die Quadrat-Operation, W die Wurzel, und das Konstrukt in der Mitte mit dem S auf dem c-Wire ist die Summenbildung der Variablen auf den beiden oberen Wires im aktuellen Zustand. Die Messoperation ist hier P, für print. Auch hier "beobachtet" man nur die Anfangszustände und die print-Ausgaben. Noch enger ist die Analogie, wenn man sich das P "destruktiv" vorstellt, d.h. die Variablen werden nach Ausgabe "gelöscht" oder auf Null gesetzt. Insgesamt also eine schöne Algorithmen-Analogie zum Verständnis der Composer-Diagramme.
An dieser Stelle ist erst einmal wieder eine Pause fällig. Wir haben Beispiele für kleine 1- und 2-Qubit Algorithmen untersucht und mittels Quantencomputer-Simulator praktisch ausprobiert. Außerdem haben wir zwei neue Gates kennen gelernt: als Entsprechung für unser G (Dreh-Feld) bei der QBIT-Box das Ry-Gate und das CNOT, das zwei Qubits verbindet. Und eine ganze Reihe neuer Begriffe, die im Sprachgebrauch der Qubit-Algorithmik verwendet werden. Es ist wieder hilfreich, sich eine tabellarische Übersicht zu machen und im weiteren Verlauf zu ergänzen. Der Anfang sei hier gemacht.
| Begriff englisch | Begriff deutsch | Bedeutung |
| Composer | Composer | Tool bzw. Form zur grafischen Darstellung von Qubit-Algorithmen |
| Circuit | Schaltkreis | Qubit-Algorithmus |
| Wire | Wire (Leitungen) | Algorithmische "Lebenslinie" eines Qubits |
| Gate | Gatter | Qubit-Operator in einem Algorithmus |
| Paramter | Parameter | Gates wie Ry können eine Parameter haben, z.B. einen Drehwinkel. |
| |0>, |1>, |a> | |0>, |1>, |a> | Schreibweise für Qubit-Zustände, alternativ zu Koordinaten |
| Basis | Basiszustand | Hier |0> oder |1> |
| Superposition | Überlagerung | (Linear-)Kombination von Qubit-Zuständen, meist von |0> und |1> |
| Hadamard-Gate | H-Gatter | Spezieller Superpositionsoperator |
| M Operator | M Operator | Mess-Operator, berechnet aus Qubit-Zuständen Wahrscheinlichkeiten von Bit-Ergebnissen |
| Classical Bit | Klassisches Bit | Messergebnisse werden als Bits / Bit-Ketten ausgegeben |
| c-Wire | c-Wire | Wire, das die Messergebnisse aufnimmt (Bit-Ketten) |
| Initial State | Anfangszustand | Jedes Qubit beginnt im Zustand |0> |
| Ry-Gate | Ry-Gatter | Eine bestimmte Art der Drehung, vergleichbar mit dem G im ZBIT-Modell |
| shots | shots | Anzahl Durchläufe eines Algorithmus für Ergebnis-Statistik |
Bevor es nun weiter geht mit Mehr-Qubit Registern, werden wir noch einige verblüffende Besonderheiten des Circuits aus Beipiel 7 untersuchen.
Stay tuned! Hier geht's weiter.